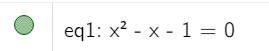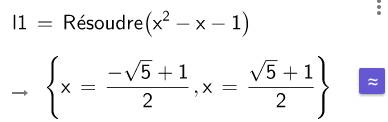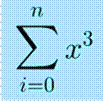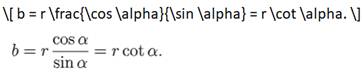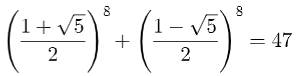|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Outils mathématiques GEOGEBRA
Capable d'animations, ce logiciel
rend la géométrie vivante et ludique. Logiciel accessible gratuitement;
il est utilisé au lycée. |
|
|
||
|
La barre des outils
Palettes des outils du type "droites" et du type "
droites particulière" |
||
|
|
|
|
|
|
|
|
>>> Calcul du volume du
tétraèdre >>>
Cercle inscrit dans le quart d'ellipse >>> Cinq
triangles dans un triangle >>>
Demi-cercles tangents – Énigme >>>
Énigme de la chèvre dans un champ rectangulaire >>>
Polygone – Inversion d'une figure polygonale >>>
Rectangle et demi-cercle (énigme) >>>
Spirale (ou escargot) de Pythagore >>>
Tangente – Trouver la pente de la tangente Et,
nombreuses constructions au fil des pages |
|

|
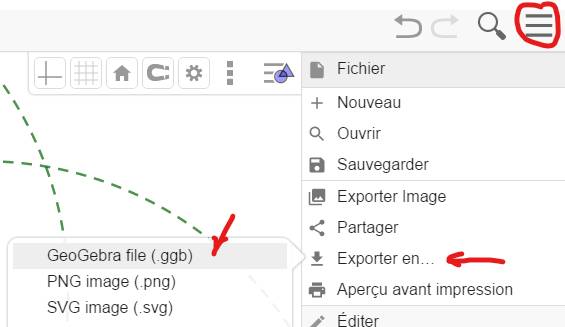
Nombreuses questions sur Internet pour savoir
pourquoi je ne retrouve pas mon travail sauvegardé. Voici la procédure à
suivre: 1)
Cliquer
sur exporter en … puis sur GeoGebra file
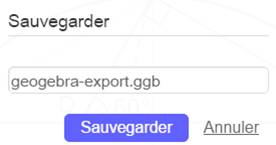
2)
Cette
fenêtre s'ouvre
3)
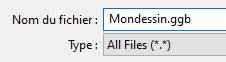
Cliquer
sur sauvegarder et taper le nom de votre fichier. C'est fait !
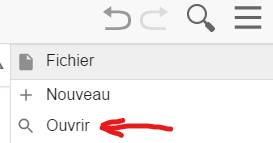
4)
POUR
RETROUVER votre travail, passer obligatoirement par la commande ouvrir dans
GeoGebra
Attention: double-cliquer sur le nom du fichier
dans le répertoire ne marche pas ! |
|
|
||
|
Mode rapide (à volonté) Appuyez
sur la touche majuscule (shift) Avec la
souris pointez l'axe: une double flèche apparait. Allongez
ou rétrécissez en bougeant la souris le long de l'axe. |
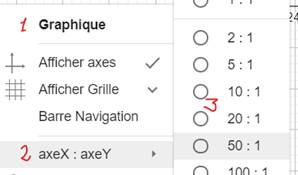
Mode menu (échelle prédéfinies) Cliquez
dans la page et obtenez cette fenêtre: Graphique: clic sur axeX : axeY et choisissez la
proportion sur les axes:
|
|
|
|
||
|
Copier une figure Pour dupliquer une figure: L'image est dupliquée sauf si les sommets sont fixés:
ancrés sur les axes, ou sommets de polygones réguliers. Alors seule
possibilité l'outil translation peu pratique si on souhaite un atterrissage
précis. |
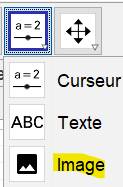
Copier une image externe Ouvrez deux fenêtres; celle de l'image et celle
de GeoGebra.
Importer une image en fichier Sans difficulté avec l'outil image. |
|
|
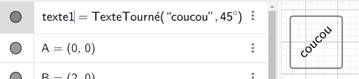
Pour orienter un texte sur une figure
taper ceci dans la zone de saisie: TexteTourné(<Texte>,
<Angle> ) Texte entre guillemets et angle en radians ou en
degré en notant 90°. |
|
|
|
|
||
|
Pour afficher le produit b, taper ce texte dans
la zone de saisie: le premier b est le nom (que vous pouvez changer); le
second b est la valeur calculée par GeoGebra (vous pouvez y mettre un produit
comme a*b); les deux nombres sont les coordonnées d'inscription du message. Le deuxième texte indique comment faire pour que
le produit suive dynamiquement le point A. |
Texte["b = " + b, (2, 2)] Texte["b = " + b, PointA] |
|
|
|
||
|
Vous avez créé un polygone régulier
et les sommets ne sont plus visibles. Ces points ne sont pas listés dans la
rubrique "Points". Comment les rendre visibles ? |
Dans la
zone de saisie, tapez simplement ceci: {Sommet(nomDuPolygone)} |
|
|
|
||
|
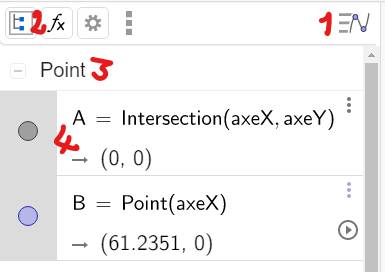
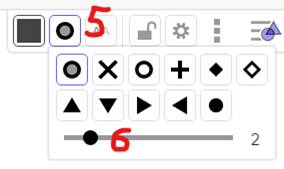
POINTS Ma figure
est construite et je veux changer la taille de tous les points. 1) Cliquer sur cette icône pour organiser la liste des objets; 2) Demander la liste par objets (type objet); 3) Cliquer sur l'en-tête de liste (tous les points sont sélectionnés et
la barre d'outils en haut à droite est disponible); 4) Option: en cliquant droit dans la liste, accès à toutes les commandes
possibles; 5) Cliquer sur le cercle; et, 6) Ajuster la taille des points. |
|
|
|
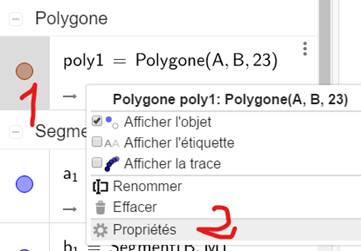
POINTS d'un OBJET Si les
points résultent de la construction d'une figure (polygones), ils ne sont pas
accessibles par la procédure indiquée. Une
commande est nécessaire (une méthode, disent les pros). 0) Après
avoir demandé l'organisation des objets par type comme indiqué ci-dessus; 1)
Cliquer droit sur le nom de l'objet (polygone) puis 2)
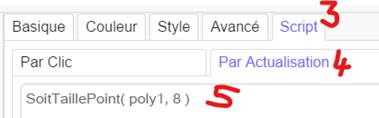
Cliquer sur propriétés; 3) En
haut à droite, aller à script; 4) Par
Actualisation 5) Mettre
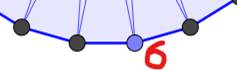
ce texte: 6) La
taille sera effective en cliquant sur un point de construction (ici, en
bleu). |
|
|
|
|
||
|
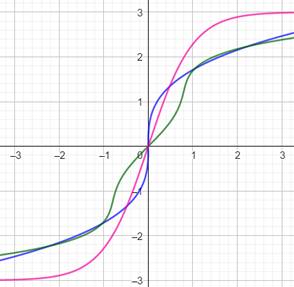
Le graphe
(ou courbe représentative) d'une fonction est obtenue immédiatement dès que
vous entrez la fonction dans la zone de saisie.
|
Courbes
d'allure sigmoïdale |
|
|
|
||
|
Assurez
vous que vous êtes bien en mode |
|
|
|
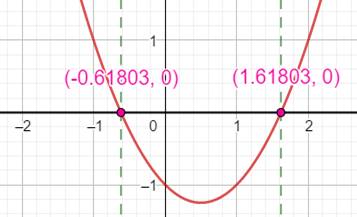
Écrivez l'équation
dans la zone de saisie, la réponse est sur le graphique
|
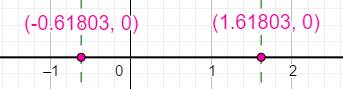
Allez
dans "Propriétés" pour afficher la valeur en chaque point. |
|
|
La courbe
en prime sans taper le "= 0" Vous entrez alors une fonction et non une
équation. |
|
|
|
En
entrant l'équation sous la commande Résoudre ( ),
vous obtenez les racines. Le petit
signe à droite, permet un calcul approché des racines. |
|
|
Voir Nombre
d'or
|
|
||
|
Ce
logiciel est utile pour écrire une formule
mathématique que vous utilisez pour votre travail ou, même, pour le
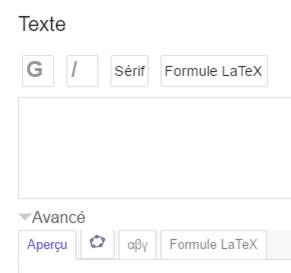
copier dans un texte. 1) Se mettre en position de déposer un texte dans la zone graphique |
|
|
|
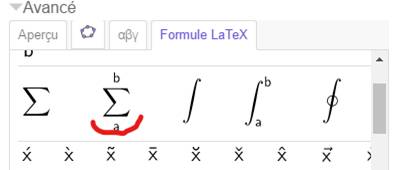
1bis) Au
besoin, cliquer sur cette icône pour ouvrir la fenêtre LaTex. |
|
|
|
2) Cette fenêtre est ouverte Note: si vous connaissez le langage LATEX, vous
pouvez écrire directement dans la zone de saisie. Sinon tous les symboles
sont à votre disposition. |
|
|
|
3) Choisissez votre symbole |
|
|
|
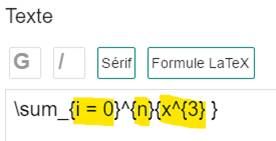
4) Un texte apparait. Il suffit de compléter à sa guise (en jaune) et la
formule est transcrite sur la zone de dessin (en bleu): Ajustez la taille avec Propriétés / Taille des caractères. |
|
|
|
5) Vous trouvez une écriture bizarre sur un site Internet. C'est sans
doute une écrire LaTeX. Un moyen commode de la
déchiffrer consiste à la copier dans la zone texte de GéoGebra |
Vous copiez le texte du haut et GeoGebra vous le transcrit comme en bas:
|
|
|
6) Exemple avec le nombre
d'or |
\left(\frac{1+\sqrt{5}}{2}\right)
^{8}+\left(\frac{1-\sqrt{5}}{2}\right) ^{8} = 47
|
|
|
|
|||
|
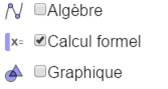
Activez
le calcul formel dans le menu principal (les trois traits). Si vous ne disposez pas de Geogebra, la
calculatrice est aussi disponible en ligne sur Internet. |
|
||
|
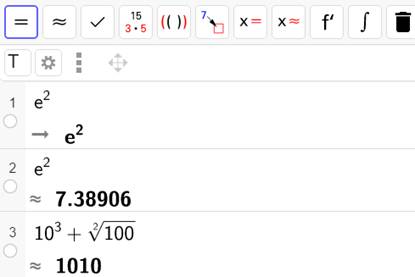
Saisissez
votre calcul avec éventuellement l'aide du clavier qui apparait dès que vous
cliquez dans la zone de saisie. S'il n'est
pas en fonction, cliquez sur le clavier miniature en bas à gauche de la
fenêtre.
|
|
||
Voir Calculatrice
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
Externe
|
GeoGebra |
Téléchargement,
tutoriels et exemples d'applications nombreux
sur Internet |
![]()