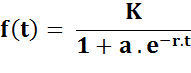|
|||||||||||||||||||||||||||||||||||
![]()
|
CROISSANCE LOGISTIQUE Fonctions logistiques De nombreux phénomènes de
croissance démarrent lentement, puis connaissent une croissance continue pour
finalement s'essouffler. On parle d'une courbe de croissance qui prend la
forme de la lettre S. |
|
|
||
|
Formulation K et r sont des réels
positifs a est un réel quelconque;
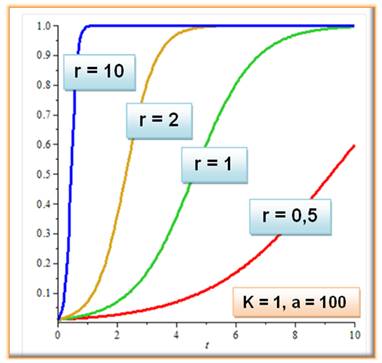
lorsqu'il est positif la courbe a la forme d'un S. Graphe Les courbes ci-contre ont
été obtenues avec K =1, a = 100 et quatre valeurs de r =
{0,5 ; 1 ; 2 ; 10}. Au départ, la courbe
logistique réagit quasiment en fonction exponentielle. Capacité d'accueil K K au numérateur est
prédominant pour de valeurs croissante de r. Avec r.t
= 10, exp(-10) = 4,5 10-5 , le numérateur est proche de
1 et la fraction devient égale à K. |
Voir Fonction sigmoïde
|
|
|
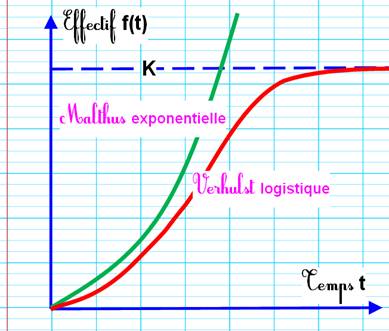
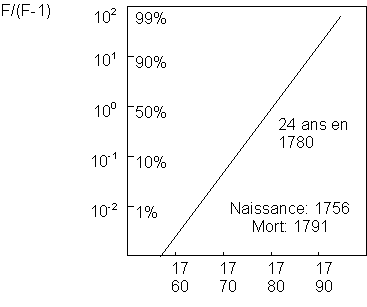
Populations Thomas Malthus (1766-1834)
prédit une croissance exponentielle
pour une population non contrainte et pour des ressources (subsistances) en croissante arithmétique, incluant des
éventuels échanges, donc, en gros, sans limites de nourriture. Pour éviter cette croissance
sans fin, il préconise la régulation des naissances. En 1844,
Pierre François Verhulst, élève d'Adolphe Quetelet, propose
cette courbe de croissance d'une population avec contrainte de ressources.
Pour lui, plus la population augmente, moins il y a de naissance et plus il y
a de morts. La surprise fut de découvrir
que parfois la situation est oscillante de façon désordonnée, chaotique. |
|
|
|
Utilisation |
Démographie / Sociologie Économie / Politique Biologie / Écologie |
|
Anglais: logistic function, logistic curve, sigmoid curve
|
|
|
|
Cette loi est très fréquente.
|
|
|
|
|
|
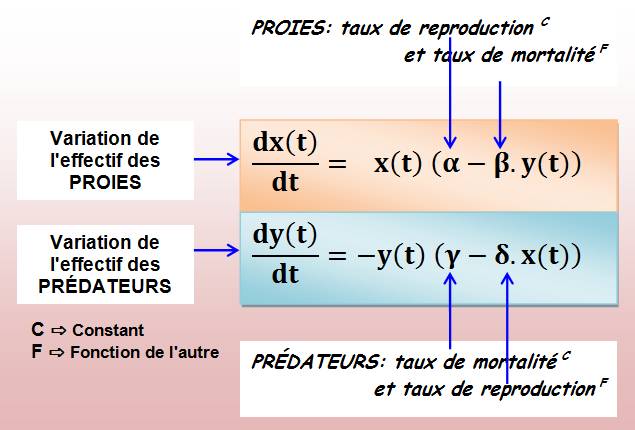
Les mathématiciens, comme Alfred Lotka
et Vito Volterra, cherchaient à modéliser la
croissance des populations animales en présence de prédateurs. Ils mirent au
point ces équations de Lotka-Volterra, dites loi ou
modèle proie-prédateurs. x(t):
effectif des proies, et y(t):
effectif des prédateurs.
Un système d'équations différentielles non-linéaires du
premier ordre. |
|
Anglais: Lotka-Volterra
equations, predator-prey (or parasite-host) model
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()