Orientation Glossaire	Atlas / Nombres et leur usage
Débutant DicoMot DicoNombre	LOGIQUE

Maître de philosophie: Par où vous plaît-il que nous commencions? Voulez-vous que je vous apprenne la logique?

Monsieur Jourdain: Qu’est-ce que c’est que cette logique ?

P: C’est elle qui enseigne les trois opérations de l’esprit.

J: Qui sont-elles, ces trois opérations de l’esprit ?

P: La première, la seconde, et la troisième;

La première est de bien concevoir par le moyen des universaux;

La seconde, de bien juger par le moyen des catégories ; et

la troisième, de bien tirer une conséquence par le moyen des figures barbara, celarent, darii, ferio, baralipton, etc.

J: Voilà des mots qui sont trop rébarbatifs. Cette logique-là ne me revient point. Apprenons autre chose qui soit plus joli.

Molière – Le Bourgeois gentilhomme (acte II, scène IV)

Voir Pensées & humour

Approche

Quelques exemples: J'ai un frère et une sœur, nous sommes les trois enfants de nos parents, c'est logique. Nous venons d'effectuer un raisonnement dont la conclusion est imparable. C'est mathématique! C'est mathématiquement logique. C'est rationnel. Tous les hommes ont de la barbe. Je suis un homme. Donc, j'ai de la barbe. C'est un raisonnement particulier, connu de l'antiquité: un syllogisme. La logique est la science des raisonnements par déductions. Chaque élément de phase indépendante est une proposition: Proposition vraie: 4 + 4 = 8; les insectes ont 6 pattes; la rose a des épines. Proposition fausse: 4 + 4 = 7; 10 est un nombre premier; Nice est en Belgique. Proposition non décidable sans autre information: J'ai un frère; il pleut; j'ai de la barbe; 2x > y. Ne sont pas des propositions: comment vas-tu? fais ce qu'il te plait; je suis plus grand; 2x + 4. La logique consiste à enchaîner les propositions vraies et/ou les propositions fausses (pas les autres) sous la forme d'un raisonnement conduisant à de nouvelles propositions jugées vraies (ou fausses) si les premières sont vraies ou fausses selon le cas. Exemples: si 2 + 2 = 4 et si 4 + 5 = 9 alors 2 + 2 + 5 = 9. Si Clément est intelligent et si tous les gens intelligents réussissent au bac, alors Clément aura son bac.

Définition

Logique du grec logikê, de logos, raison. Science du raisonnement en lui-même, abstraction faite de la matière à laquelle il s'applique et de tout processus psychologique. Science générale des déductions (inférences). La logique fixe les règles de déduction qui permettent de valider le bien-fondé logique de propositions, et cela, indépendamment de leur véracité, de la justesse, de leur contenu par rapport à la réalité. La validité d’un argument doit être distinguée de la vérité de la conclusion.

Principe

Le langage courant peut prêter à des malentendus ou des confusions. En mathématique, on a fait le choix de traduire les propositions en langage artificiel et formel ne contenant que les termes logiques significatifs du langage courant. La logique constitue une langue, c'est-à-dire un système de signes avec les règles de leur emploi. Cette langue ne considère que les propositions vraies et les propositions fausses (principe de la double valeur). Cette langue est constituée d'un système de symboles et de variables liés par des opérateurs (connecteurs) qui déterminent la structure interne des propositions et les relations entre les propositions. Par exemple: Vrai, faux, et , ou, si…alors …, …

Domaine de la logique et ses sous-domaines

(Explications ci-dessous)

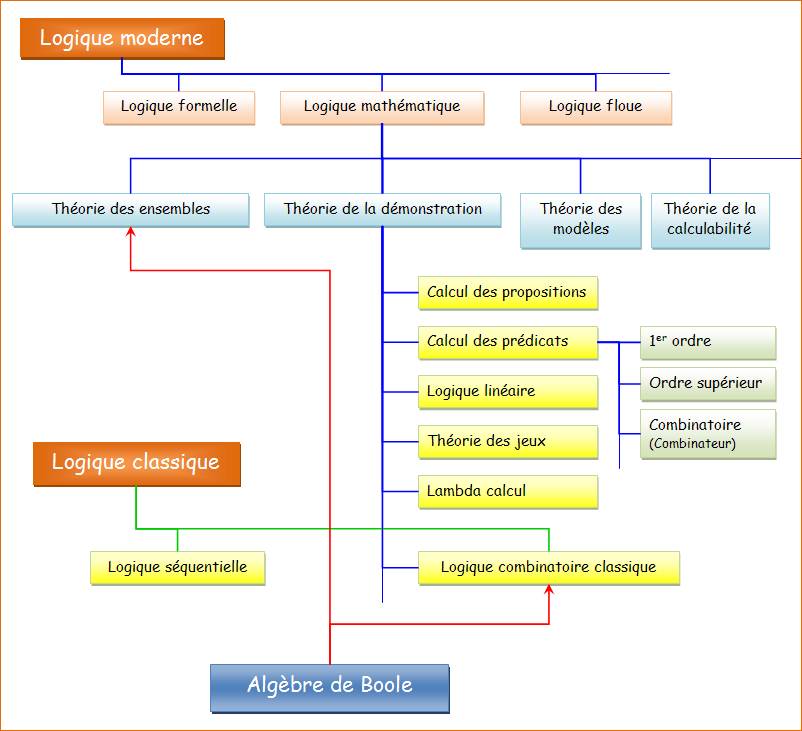
Tentative de synthèse à partir de Larousse, Universalis, Pochothèque, sans oublier Wikipédia

En bref

La logique est l'art de raisonner. Si elle existe depuis Aristote, c'est Frege qui, en s'appuyant sur une approche mathématique, a créé la logique moderne, l'utilisation d'un lange formel, le calcul des propositions et le calcul des prédicats. En logique, la syntaxe s'intéresse à reconnaitre les énoncés bien écrits, alors que la sémantique s'occupe de la signification de ces énoncés, et notamment de leur valeur de vérité. La logique est indispensable, notamment dans la théorie de la démonstration.

Logicisme

Les mathématiques sont une extension de la logique. Tous les concepts et toutes les théories mathématiques sont réductibles à la logique. Approche développé par Gottlob Frege et adoptée par Bertrand Russell et Alfred North Whitehead.

Logique FORMELLE

Logique formelle ou symbolique: étude générale des raisonnements déductifs, abstraction faite de leur application à des cas particuliers. La logique formelle étudie la validité des arguments et les conditions sous lesquelles une conclusion peut être inférée de manière valide à partir de prémisses. Note: La logique formelle n'est pas l'épistémologie des maths.

Logique MATHE-MATIQUE

Logique mathématique: science qui étudie les raisonnements, les concepts et les valeurs de vérité des propositions. Cette science, qui est à la base de la formalisation des différents domaines mathématiques, ne s’intéresse pas au contenu des objets étudiés mais à leur structure formelle. La logique mathématique définit et étudie les représentations formelles du langage mathématique. Ses objets fondamentaux sont: les formules modélisant les énoncés mathématiques, les dérivations modélisant les raisonnements mathématiques et les sémantiques établissant les liens entre ces modèles et les objets qu'ils sont censés représenter.

Logique FLOUE

La logique classique s'appuie sur deux états; la logique ternaire, sur trois états Par contre, la logique floue introduit plusieurs niveaux de gradation dans l'appréciation d'une grandeur et traite ces nuances de manière appropriée.

Théorie de la DÉMON-STRATION

La théorie de la démonstration, ou théorie de la preuve (anglais: proof theory), regroupe tous les théories axiomatiques qui assurent la cohérence des mathématiques. Du calcul des propositions à la linguistique en passant par le lambda calcul et bien d'autres … C'est la logique de la logique!

Calcul des PROPO-SITIONS

Calcul des propositions ou calcul propositionnel: comme son nom l'indique, il s'agit de formaliser un raisonnement fait de phrases (propositions) qui s'enchainent. Système formel constitué de variables appelées propositions, et de connecteurs: => qui signifie si..., alors... , non est la négation d’une proposition, Conjonction équivalent à ET, Disjonction équivalent à OU. Il existe également des axiomes qui permettent de dire si une formule est un théorème, c’est-à-dire une combinaison plus ou moins complexe d’axiomes. Le calcul propositionnel constitue l’une des bases du développement de l’informatique théorique.

Calcul des PRÉDICATS

Il s'agit d'un calcul propositionnel plus poussé utilisant les quantificateurs: "il existe x" et "pour tout y". On y définit la notion d'individu, objet d'un ensemble prédéfini; et celle de prédicat, relation sur cet ensemble d'individus. Un prédicat composé d'un seul argument est une propriété.

Théorie des ENSEMBLES

La théorie des ensembles est une branche des mathématiques fondée au XIX^e siècle par le mathématicien allemand Georg Cantor, qui introduit la notion d’ensemble à l’aide d’axiomes. Notion d'appartenance à un ensemble, à la réunion de plusieurs ensembles, à leur intersection …

Logique COMBI-NATOIRE

La logique combinatoire est la logique classique utilisée dans les ordinateurs et autres appareils numériques. Elle repose sur l'utilisation de relations entre variables du type NON, ET, OU … définies par une table de vérité et répondant aux principes de l'algèbre de Boole (anglais: combinational, digital logic, boolean circuits). Note: ne pas confondre avec la combinatoire des "combinateur" (anglais : combinatory) une théorie avancée de la logique moderne..

Logique SÉQUEN-TIELLE

La logique séquentielle est une logique combinatoire dont les états de sortie dépendent des états d'entrée (comme en combinatoire) et aussi des états antérieurs du système. L'historique des états du système est mémorisé au moyen de mémoires de type bascules ou registres. Le système est cadencé par une horloge ou à l'aide de monostable (circuit qui maintient un signal à 1 pendant un temps défini). Application aux automates.

Algèbre de BOOLE

La L'algèbre de Boole est utilisé dans le domaine de la logique mathématique comme dans le domaine de la théorie des ensembles. La théorie des ensembles comme le calcul des propositions utilisent des lois semblables. L'algèbre de Boole généralise ces lois au profit d'une mathématique abstraite. Cette notion fut développée par George Boole dès 1847 puis complétée par A. De Morgan. Les lois et les propriétés de l'algèbre de Boole sont analogues à celles de l'algèbre classique. L'algèbre de Boole sert de base aux opérations mises en œuvre dans les circuits d'ordinateurs ou dans les logiciels tels ceux utilisés par les moteurs de recherche sur Internet. Algèbre utilisée dans plusieurs branches des mathématiques: algèbre, théorie des ensembles ordonnés, calcul des probabilités, logique combinatoire.

Vocabulaire

Inférence: Opération intellectuelle par laquelle on passe d'une vérité à une autre vérité, jugée telle en raison de son lien avec la première. La déduction est une inférence. Règles d'inférence, celles qui permettent, dans une théorie déductive, de conclure à la vérité d'une proposition à partir d'une ou de plusieurs propositions, prises comme hypothèses. Prédicat: attribut affirmé ou nié d'un sujet. Calcul des prédicats : partie de la logique qui traite des propriétés générales des propositions analysées en prédicats. Prémisse: chacune des deux premières propositions d'un syllogisme (la majeure et la mineure). Relation: un prédicat à plusieurs variables. L'égalité (=) est une relation à deux variables ou relation binaire. Théorie des relations : partie fondamentale de la logique moderne, comprenant le calcul des relations et l'étude des divers types de relations et de leurs propriétés générales. On étudie notamment les relations d'équivalence et d'ordre. Valeur de vérité: elles sont au nombre de deux: le vrai et le faux. Elles sont assignées aux propositions élémentaires de manière analogue à l'assignation de valeurs numériques aux expressions algébriques.

Anglais

Logic: the study and art of reasoning correctly. Study of the structure of sound arguments. Deductive logic deals with "watertight" arguments relating a conclusion to its premises or starting assumptions. Logically equivalent: two compound statements involving the same components are logically equivalent if they have the same truth table. This means that, for all possible truth values of the components, the resulting truth table value of the two statements are the same. Boolean algebra: both sets and propositions satisfy similar laws. These laws are used to define an abstract mathematical structure called Boolean algebra, which is named after the mathematician George Boole (1813-1864).

Voir	Algorithme Électronique Énigme d'Einstein Intelligence artificielle Interdictions Lambda calcul Les trois dieux – Énigme Linguistique – Index Logique – Débutant Logique en bref: proposition ou prédicat ? Logique – Historique Logique – Index Logique combinatoire Logique floue Menteurs et Véridiques – Énigmes Outils de la logique – Diagramme de Karnaugh Paradoxes Phrases en autoréférences Programmation – Index Raisonnements Syllogismes Tiers exclu
Aussi	Forme d'esprit Jeux et énigmes– Index Langue et littérature – Index Mathématiques en mots Nombre et autour du nombre Nombres dans toutes les langues Pensées et Humour
Cette page	http://villemin.gerard.free.fr/Referenc/Vocabula/GlosL/Logique.htm