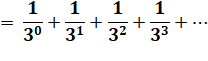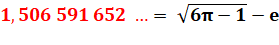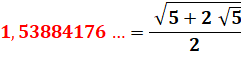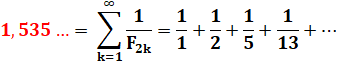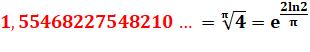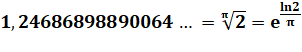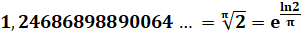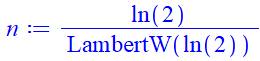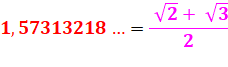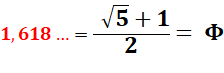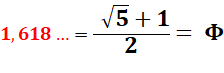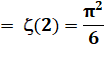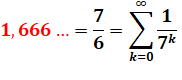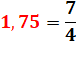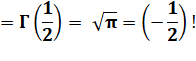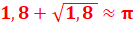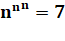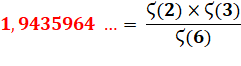nombre – de un et demi à deux

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 06/11/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES			Glossaire Nombres
0,9 0,5 0,1 0,01 0,001 0	1			2 / 3 4 / 5 6 / 7 / 8 / 9 10 / 15 20 / 50 100 / 500 1000
Nombre 1	Culture 1	Maths 1	De 1 à 1,5	Expressions en 1
Débutant 1	Culture 1 suite	Unité	De 1,5 à 1,9	Proverbes en 1
Quiz 1	Quantité 1	Racines de 1	Fractions = 1
	Sciences		Fractions Unitaires

Nombres de 1,5 à 1,9

Un aphorisme est soit une demi-vérité

soit une vérité et demie

Karl Kraus

Voir Pensées & humour

3 / 2 = 1,5

TintinHadock

Les aventures de Tintin – Le Temple du Soleil – Hergé – Casterman - 1949

1,5

Nombre	1,5 = 1 ½ Sesqui.	>>>
Unité	1,5 litre = 1 magnum	>>>

1,5 = 3/2

Somme des inverses des puissances de 3.

Note: 3/2 et 5/2 noms pour les étudiants en prépa.

Vitesse de convergence (i la puissance de 3, N le nombre et Qté, la quantité de 9):

i N Qté

4 1, 493 1

12 1, 4999990 5

23 1, 499999999994 10

107 1, 49999999999…996 50

1,5 = 1 + 1/2

1,8333 = 1 + 1/2 + 1/3

2,08333 = 1 + 1/2 + 1/3 + 1/4

= 1 + 1/2 + 1/3 + 1/4 …

Nombre harmonique.

La suite harmonique est lentement divergente. Il faut 10⁴³⁴ termes pour atteindre la somme de 1 000.

Biologie

1,5 m

Longueur chez l'homme de la molécule d'ADN déroulée.

>>>

	Approximation de 3/2
1,506 591 884 9 (28)	Aire de la fractale de Mandelbrot. Estimation statistique (comptage des pixels) réalisée par Thorsten Förstemann en 2012. Robert Mufano présente une estimation très proche de celle-ci en 2012. Aire souvent approximée par le nombre ci-dessus. Mais, ce nombre n'est pas la valeur exacte de l'aire.
1,5246999605 3809435992 3363575688 4211622202 236231 …^{2^n}	Le plancher de ce produit le prochain nombre premier plus grand que le carré du nombre premier précédent. Ex: n = 3, cette constante à la puissance 8 donne 29 qui est le carré juste supérieur à 5². Liste: 2, 5, 29, 853, 727613, 529420677791, … OEIS A059784
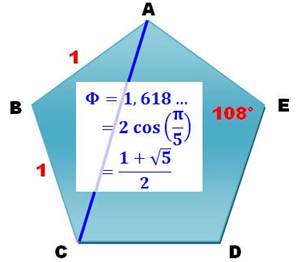
1,528 946 355 …	Racine de x⁵ – 2x⁴ + x³ – 1 Voir Pions noirs et blancs
	Deux valeurs proches à 4 pour 1000. Celle du bas est la longueur de la hauteur d'un pentagone régulier de côté unité. Celle du haut est la longueur de la hauteur d'un pentagone approché de côté unité dont la construction est particulièrement simple.
`= 1,5353705088362529850...`		Constante des inverses pairs de Fibonacci (sums of reciprocals of even-indexed Fibonacci numbers).
1,551 387 524 55...	Racine de 2x³ – 2x² – 3x + 2 = 0 Voir Triangle de Calabi
			Racine pi-ème de 4. Racine pi-ème de 2.
1,55961046946236… = x x^x = 2	Nombre transcendant. Résolution de l'équation nⁿ = 2. Pas simple à résoudre. La solution littérale s'écrit (avec W, la fonction W de Lambert):
1,561552813… =	Racine triangulaire de 2.
1,570796327… =	Valeur en radian de l'angle droit (90°).
	Nombre irrationnel.
1,584962501… = log₂(3) = ln(3) / ln(2)

1,6

Unités

1, 609 344 km dans un mile (proche du nombre d'or).

Calculs pratiques avec la suite de Fibonacci:

Sciences

1,615 Limite de la somme du maillage cristallographique.

			Proche du nombre d'or à 0,00187… près.
			Nombre d'or, diagonale du pentagone. Nombre métallique n°1. 1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911375 …
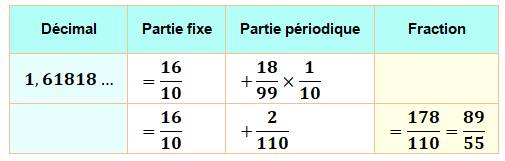
1, 618034² = 2,6180034… = 2, 618 034 025 156		Anagramme numérique. En laissant de côté les dernières décimales.
1,6181818… = 55/89	Fraction approximant le nombre d'or. Méthode de calcul de la fraction Voir Explications

1,619 9...	Constante impliquée dans la comparaison des cubes et des sphères. 1, 6119919540 1646964071 6966846639 2849389446 1407232386 1555692292 0753789509 6505714527 4246155649 7395024339
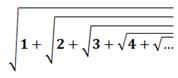
1,632526 … =	Racine de 2 à la puissance racine de 2; irrationnel
		Dimension de la fractale du mot Fibonacci. Phi est le nombre d'or.
1,644 … = 1/1² + 1/2² + 1/3² + 1/4² + ... = 2²/(2²-1) x 3²/(3²-1) x 5²/(5²-1) x …	Zêta (2), constante avec Pi. Limite de la fonction de Riemann d'ordre 2. Somme des inverses des carrés (1/n²) Produit des premiers au carré sur lui-même diminué d'une unité Voir Suite et valeur en Identité d'Euler/ Démonstration d'Euler
1,660964048… = log(10) / log(4)	Nombre parfait: le ratio entre p (la puissance de 2) et la quantité de chiffres Q du nombre parfait approche log(10) / log(4). Pour le plus grand connu en 2016 (P₄₉), on a p = 74 207 281 et Q = 44 677 235 et p/Q = 1,660964046…
			Constante de récurrence quadratique de Somos. Racines continues.
	Constantes que l'on retrouve dans la formulation des constantes trigonométriques.
1, 666 = 5 / 3	Fraction Voir Nombre 1,1666…
	Somme des inverses des puissances de 7.

1,7

Biologie

1,7 plus de matière organique produite par

un mélange d'espèces que par une espèce unique. Étude 2007. Montre l'intérêt de la biodiversité.

		Proche de racine de 3.
		Approximation de racine de 3, en septièmes
1,720477401… = 5/4 x tg (54°)			Aire du pentagone = 1,720 …a².
1,732050808 … = 3		Racine carrée de trois. Approximation par 97/56 ou 265/153. Diagonale du cube unité.
1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 1690880003 7081146186 7572485756…					Cent premières décimales de racine de 3.
		Valeur à retenir en trigonométrie.
				Relation trigonométrique.
= 1,7320… 7+3+2+0+…6+5+5+5 = 666 = 1,2457… 2+4+5+7+…+ 7+0+8+8 = 666	La somme de ses 145 premières décimales est égale à 666, ce qui en fait un nombre du diable. Idem pour la racine cinquième avec 140 décimales.
1,732142857 … = 97 / 56 0,000092049		Bonne approximation de racine de 3. Valeur de l'écart.
		Approximation en 127^e.
		Racines avec décimales proches à 0,00008… près.
1,7… = 21 / 12 2,6… = 321 / 123 3,5… = 4321 / 1234 etc.		Division d'un nombre par son retourné. Les deux premiers chiffres significatifs du quotient: le premier vaut le premier chiffre de gauche moins 1, et le second est son complément à 8.
		Fraction
1,754 877 666 24...		Racine de x³ - 2x² + x - 1 = 0 Voir Triangle de Calabi.
1,757 932 756 61 … =		Constante des racines emboitées
1,7632228343519... = n & nⁿ = e		Inverse de la fonction W de Lambert (ou Oméga) pour e. Non exprimable avec des fonctions élémentaires.

Social

1,77 m et 1,65 m

Taille moyenne des hommes et des femmes en 2000.

>>>

1,77245385090552 …

Fonction Gamma d'Euler.

Nombre transcendant.

Aire sous la courbe de Gauss de hauteur unité et d'écart type unité.

Multimédia

1,777… = 16 / 9

Un des formats des écrans de télévision.

>>>

e^c = 1, 781 072 417 9...

e^-c = 0, 561 …

Exponentielles de la constante d'Euler.
Avec: gamma = 0,577…

1,7822139 … =

Valeur de la constante de Grothendieck, conjecturée par Jean-Louis Krivine. Démontré comme borne supérieure en 2011. Valeur min = 1,677…

1,794…

Constante de percolation de la rigidité. Phénomène intervenant dans la recherche des graphes rigides.

1,8

	Approximation de Pi à 1,5 pour 100 000 (0,000048). Construction géométrique de cette valeur par Thomas Hobbes vers 1600. Valeur retrouvée vers 1900 par Ramanujan.
1,805 5… = 65 / 36	Égal une somme infinie: 5/13 + 55/13² + …
1,833 3… = 5 / 6 = 1/1 + 1/2 + 1/3	Nombre harmonique.
1,839 286 …	Constante de tribonacci.

Cinéma

1,85 Un des formats des écrans de cinéma.

>>>

1.85540442929… = n

Troisième hyper racine de 7.

1,9

1,902 160 ...	Somme des inverses des nombres premiers jumeaux, dite somme de Brun.
	La somme des inverses des nombres puissants converge vers cette constante.

Social

1,92 taux de fécondité des femmes en France en 2005

2,08 en 2012

>>>

Suite

Voir le menu en haut de page

Culture en 2

Racines – Table

Voir

Débutants – Index

Départ de nombreuses suites

Nombres – Glossaire

Premier nombre géométrique

Cette page

http://villemin.gerard.free.fr/NombDico/UnP22.htm