NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/03/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Chaos
Débutants Général	Chaos & complexité				Glossaire Général
INDEX Chaos	Complexité	Chaos	Suite Logistique	Loi logistique
		Sommaire de cette page >>> Loi logistique >>> Fractales de Mandelbrot

SUITE LOGISTIQUE

Que devient une population en présence de plus ou moins de nourriture? Dans certain cas l'évolution est imprévisible, chaotique!

Trois cas classiques:

La suite logistique modélise l'évolution discrète de la population (d'années en années par exemple);

La loi logistique modélise l'évolution continue de la population; et

La loi proie-prédateurs modélise l'évolution en présence de prédateurs.

Le terme logistique se rapporte au calcul (logistikos en grec). Nous n'en savons pas plus sur la raison de ce choix par Verhulst en 1845.

Anglais: Logistic map

En bref – Dennis Sullivan, prix Abel 2022

À partir de la fin des années 1970, le chercheur américain Dennis Sullivan s’intéresse aux systèmes dynamiques, dont un grand nombre présentent des comportements chaotiques.

L’un d’eux est connu sous le nom de suite logistique, qui décrit par exemple l’évolution d’une population animale d’une année sur l’autre. Cette suite est définie par x_n+1 = μ x_n (1 – x_n). Son comportement dépend de façon très sensible de la valeur du paramètre μ.

Si 0 < μ < 1, la population finit par tomber à zéro.

Pour μ entre 1 et 3, la population se stabilise à une certaine valeur après une phase transitoire.

Puis, entre 3 et environ 3,45, la population oscille entre deux valeurs suivant un cycle de deux ans.

Entre 3,45 et environ 3,54, le cycle passe à quatre ans, puis à huit ans, etc.

À partir de μ proche de 3,57, le comportement devient chaotique.

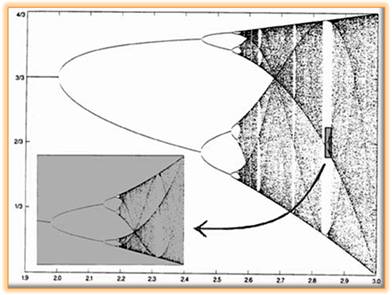
Quand on trace ces valeurs de populations en fonction du paramètre μ, on observe des bifurcations.

Le physicien Mitchell Feigenbaum a découvert une propriété étonnante : la distance entre deux bifurcations successives converge vers une valeur fixe qui vaut environ 4,6692… Cette constante de Feigenbaum se retrouve dans de nombreux systèmes et présente un caractère universel, indépendant des détails du système. Dennis Sullivan a démontré ce caractère universel.

Dans le domaine des systèmes dynamiques à variables complexes, certaines suites tracent des figures fractales. En 1985, Dennis Sullivan démontre une conjecture formulée dans les années 1920 par Pierre Fatou, qui indique que dans ces systèmes certaines orbites  (les valeurs successives prises par la suite) reviennent vers leur point de départ au lieu de s’éloigner pour toujours.

Par ailleurs, au début des années 2000, le Sullivan revient dans le domaine de la topologie et met en évidence un nouvel invariant pour une variété basée sur des boucles. Depuis, il s’intéresse à la dynamique des fluides et comment utiliser les outils de la topologie pour les étudier.

Source: Pour la science: Prix Abel 2022 : Dennis Sullivan récompensé – Sean Bailly – 28 mars 2022

SUITE LOGISTIQUE
Formulation
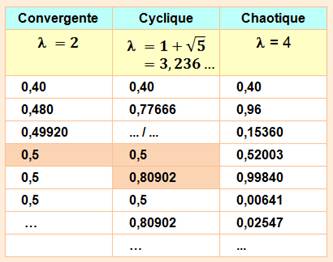
Elle caractérise de nombreux phénomènes de croissance sous contrainte, comme une population de bactéries avec un quota de nourriture donné. On étudie la loi logistique pour différentes valeurs de départ (x0) et pour différentes valeurs du coefficient d'amplification ()	La loi se comporter de différentes manières selon la valeur de lambda:
La courbe ci-contre montre les zones de transitions, de ruptures. Les courbes de la page suivante illustrent les comportements pour x0 = 0,4 et pour une variation en . Feigenbaum a montré que, après un nombre suffisant d'itérations, les motifs se répètent (zoom) avec une échelle de forme toujours la même: 2,502908 et 4,66920166.	Diagramme de bifurcation Source: Strange attractor
Exemple typique de complexité chaotique. Souvent donnée comme exercice de programmation.	Révélée par Robert May en 1976. Solution discrète de la loi logistique de Verhulst.

Voir Dédoublement / Coefficient d'étirement

FRACTALES DE MANDELBROT
C'est avec une loi semblable zn+1 = . zn ² + k, mais dans le domaine des nombres complexes, que l'on construit les fractales de Mandelbrot et de Julia, fractales dites du " pou ". Pour construire ces fractales, l'idée est de dessiner un point noir pour les points pour lesquels la valeur de z converge; et, un point blanc où ça diverge (ou alors des couleurs selon la vitesse de divergence).

Le théorème de période trois

En 1973, Tien-Yien Li et James York découvre que les systèmes tels que: les populations de molécules, d'insectes, de personnes... se comportent d'une manière remarquable. Dans une séquence de trois générations dont deux avec une population croissante puis si le niveau revient à son niveau de départ ou à un niveau inférieur, alors le système est chaotique, c'est-à-dire imprédictible. Si on prend le modèle de l'attracteur étrange pour deux populations voisines, il y a trois possibilités: ou elles restent voisines sur la boucle de départ, ou elles partent toutes les deux sur la boucle voisine, ou l'une reste sur la boucle de départ et l'autre part sur la boucle voisine.

Suite	Loi logistique Entropie (thermodynamique) Catastrophes Les 17 équations qui ont changé le monde Suites
Voir	Attracteurs Complexité Complexité de Kolmogorov Crises des maths Croissance chaotique Fractales Lapins de Fibonacci Les trois corps Lorenz Lune Notions de la physique moderne Sciences – Index
Sites	Period Three Implies Chaos – Tien-Yien Li et James A. Yorke Matlab Fun (pdf) – For Loops, Iterative Equations, and the Logistic Map – Exemple de programmation The logistic map revisited – Exemples complets avec animations
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Chaos/LoiLogis.htm