|
Édition du: 27/12/2024 |
|
INDEX |
Bilan de connaissances en maths Domaines avancés |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Les pavages
apériodiques d'Ammann-Beenker admettent des cycles hamiltoniens,
contrairement aux pavages apériodiques de
Penrose, de quoi relier les atomes de certains quasi-cristaux de façon
optimale. Démontré en mi-2024. |
||
|
|
Sommaire de cette page >>> Un résumé en images >>> Approche: cycle hamiltonien >>> Pavage périodique ou apériodique >>> Pavage d'Ammann-Beenker >>> Difficulté du problème |
Débutants Glossaire |
|
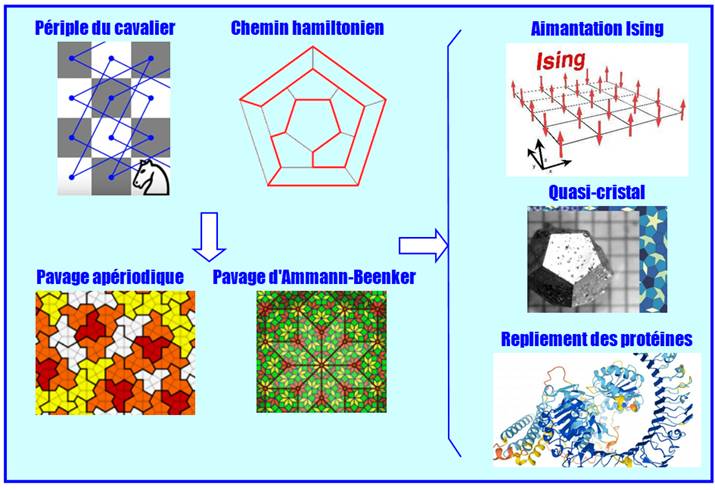
Comment révéler la structure interne de certains matériaux
complexes ? Une solution: la
modélisation par un graphe dont on étudiera les propriétés. Notamment
l'existence de chemins particuliers en boucle nommés chemins hamiltoniens. |
|
Cavalier Dans le problème du périple du cavalier
aux échecs, le cavalier visite chaque case d'un échiquier exactement une fois
avant de revenir à sa place de départ. Il s'agit d'un exemple de cycle hamiltonien: un chemin en boucle à travers un
quadrillage visitant chaque sommet une fois et une seule fois. Voyageur de commerce Le problème du voyageur de
commerce consiste à déterminer le trajet optimal pour visiter un certain
nombre de villes et retourner au point de départ sans emprunter deux fois la
même route. Cette question revient à se demander si le graphe
représentant les villes (les sommets) et les routes les reliant (les arêtes)
possède ou non un cycle dit hamiltonien. |
Importance du cycle hamiltonien L'étude des cycles hamiltoniens date au moins au
IXe siècle, lorsque le poète indien Rudra a composé un poème basé
sur le périple du cavalier. Depuis lors, ils sont apparus dans une variété
d'applications dans les sciences et les mathématiques. Problème NP-complet Dans le cas général, c’est un problème difficile.
Il est même « NP-complet
», ce qui signifie que le temps nécessaire pour déterminer si un graphe
possède un cycle hamiltonien croît exponentiellement avec le nombre de
sommets. |
|
|
Pavage du plan Un pavage est un
recouvrement du plan, complet et sans chevauchement. Il est réalisé à l'aide de tuiles de base
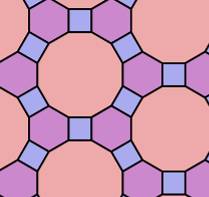
assemblées façon puzzle. Pavage périodique Pour recouvrir une surface sans laisser de trous,
l’option la plus simple consiste à utiliser un pavage périodique où les tuiles sont agencées de manière régulière
et répétée. |
Pavage périodique avec trois sortes
de tuiles
|
|
|
Pavage apériodique Les pavages apériodiques sont tels qu'il n'existe
aucune symétrie
de translation
parmi les motifs réalisés par le pavage. Pavage apériodique de Penrose Les plus connus sont les pavages
de Penrose, qui utilisent deux motifs élémentaires, un quadrilatère
convexe (le cerf-volant) et un quadrilatère concave (la fléchette). Pavage apériodique d'Ammann-Beenker En1970, Robert Ammann (1946-1994) découvre cinq
exemples de pavages comme celui présenté à droite. Même découverte indépendamment par Beenker , même
si la méthode de construction diffère (substitution pour le premier et projection
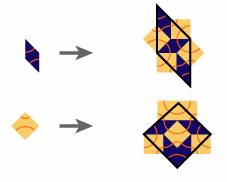
pour l'autre). Les pavages d’Ammann-Beenker sont des pavages
apériodiques du plan par un carré et un losange à angle de 45°. Présentant
une 8-symétrie (locale), ils sont devenus un modèle classique des
8-quasi-cristaux. Règle de substitution
Le facteur de substitution vaut 1 + √2, le nombre
d'argent. |
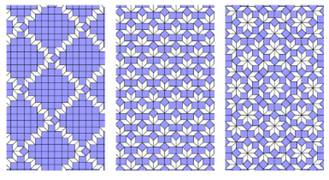
Pavage d'Ammann-Beenker de type A5
Motif de base du pavage A5 Trois types de pavage A-B
|
|
|
Historique |
||
|
Historique Au cours du temps, différentes méthodes pour
composer des pavages ont été proposées : règles de mise en correspondance, substitutions,
schémas de coupe, etc. Dès les années 1980, les pavages A-B ont trouvé
leur utilité en physique, car ils s’appliquent aux structures de certains
quasi-cristaux. En 1987, Wang, Chen et Kuo (Beijing) ont annoncé
la découverte d'un quasi cristal à symétrie octogonale. Ils ont découvert que
la figure de diffraction (qui est liée à l’agencement des atomes) d’un
alliage de vanadium-nickel-silicium et de chrome-nickel-silicium rappelle les
motifs d’Ammann-Beenker En mi-2024, Shobhna Singh et ses collègues
(université de Cardiff) ont mis au point une méthode pour trouver un cycle hamiltonien sur de tels pavages, quelle que soit
leur taille. |
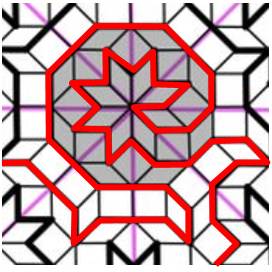
Cycle Hamiltonien (en rouge) sur
pavage A-B
|
|
|
Genèse de la découverte de 2024 Pour comprendre les propriétés des quasi-cristaux,
les physiciens doivent s’intéresser aux spécificités des motifs apériodiques,
notamment à l’existence ou non d’un cycle hamiltonien
reliant tous les sommets d’un pavage ou, de manière équivalente, tous les
atomes d’un quasi-cristal. En 2020, on démontre que les pavages de Penrose
n'admettent pas de cycle hamiltonien, mais la question pour les pavages
d’Ammann-Beenker restait entière… Jusqu’aux travaux de Shobhna Singh et ses
collègues en 2024 qui, d’une part, prouvent qu'un chemin hamiltonien existe
bien dans ces pavages A-B et, d’autre part, donnent un algorithme pour les
construire, dont le temps d’exécution cette fois-ci ne croît pas de façon
exponentielle avec le nombre de sommets. Le problème de la recherche des cycles
hamiltoniens dans les contextes généraux est si difficile que sa solution
résoudrait automatiquement de nombreux problèmes ouverts importants dans les
sciences et les mathématiques. |
Intérêt Les structures de boucle géométriques fractales
sont omniprésentes en physique. Voir illustration Elles apparaissant souvent dans les modèles de
phénomènes critiques, comme:
Le cas de certains quasi-cristaux constitue un
cas particulier dans lequel le problème semble plus simple. |
|
|
Recherche d'un chemin hamiltonien dans
le pavage A-B Dans le cas général, c’est un problème difficile,
NP-complet. Mais dans certains cas particuliers, le problème
est plus simple que prévu. C’est par exemple le cas des graphes construits
sur les pavages apériodiques d’Ammann-Beenker. Shobhna Singh
et ses collègues ont mis au point une méthode pour trouver un cycle
hamiltonien sur de tels pavages, peu importe leur taille. Ils disent: Nous montrons que certains quasi-cristaux
constituent un cas particulier dans lequel le problème est étonnamment simple.
Par conséquent, dans ce contexte, nous résolvons certains problèmes
apparemment impossibles à traiter. Nos résultats ouvrent la possibilité de traduire
une multitude de problèmes à désormais étudier dans un nouveau cadre. |
Labyrinthes complexes Ici, il s'agit de construire des cycles
hamiltoniens dans des structures irrégulières infiniment grandes comme celles
décrivant la matière exotique connue sous le nom de quasi-cristal. Les chemins qui en résultent forment des
labyrinthes incroyablement complexes. Par exemple, les molécules flexibles peuvent
traverser ces lamages pour se coller parfaitement sur des surfaces
quasi-cristallines, transformant les quasi-cristaux en catalyseurs, lesquels
augmentent l'efficacité industrielle en abaissant l'énergie des réactions
chimiques. D'une manière générale Le problème de la recherche des cycles
hamiltoniens dans le contexte général est si difficile que sa solution
résoudrait automatiquement de nombreux problèmes ouverts importants dans les
sciences et les mathématiques. |
|
Illustration

Dans ce pavage d'Ammann-Beenker des carrés et des
losanges
remplissent un espace 2D avec un motif organisé qui ne
se répète jamais intégralement.
Illustration de l'aspect
fractal
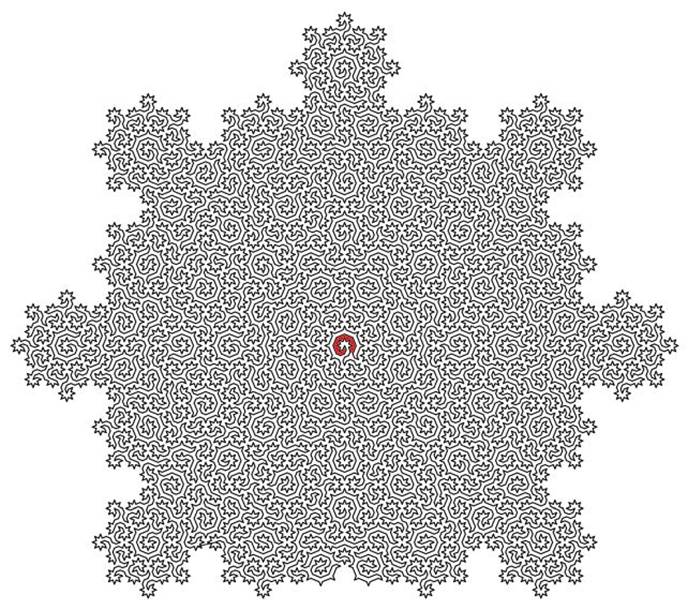
Le cycle hamiltonien sur ce pavage d'Ammann-Beenker
crée un labyrinthe
fractal
Source Université de Bristol
Détail de la zone centrale

Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Article |
|
|
Sites |
|
|
Cette page |