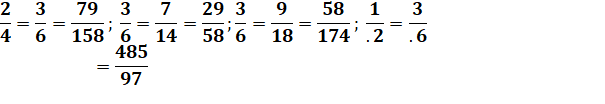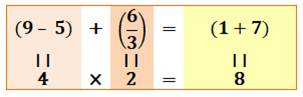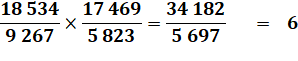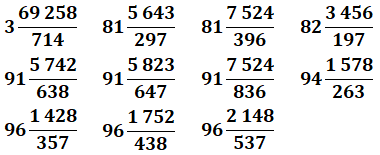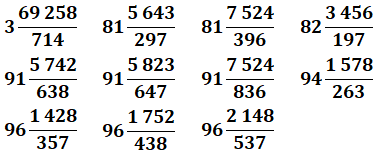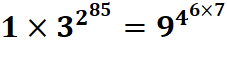Nombres pannumériques, formés de tous les chiffres

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/12/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres à motifs
Débutants Général	PANNUMÉRIQUES			Glossaire Général
INDEX En chiffres Motifs Magie Chiffres	Pannumériques	Nombres & Carrés PN	Produits PN
	123 456 789	381 654 729	PN & Repdigits
	Somme Pannum.	Fractions minimales	100 et autres pannum.
	Semi-pannumériques	Pannumériques divisibles	Problème CE2 Vietnam
	n avec tous les chiffres	Anneaux Olympiques	Fractions
	Carré magique 3x3	Pi et e en pannumérique	Division
	Concaténation	Divisibilité par 11	Multiplication
	Progression Arithm.	Divisibilité de 2 à 18
		Sommaire de cette page >>> Amusements typiquement pannumériques >>> Unités des puissances >>> Pannumériques qui le restent par division >>> Quelques jeux pannumériques >>> Nombre 123 456 789 >>> Analyse des pannumériques >>> Curiosités avec 123456789 >>> 102345698 7 896543201 >>> Carrés magiques pannumériques >>> Formule donnant les pannumériques >>> Multiplications pannumériques >>> Somme algébrique des chiffres >>> Pannumériques premiers >>> Fractions pannumériques >>> Pannumériques en base b >>> Jeux de premiers pannumériques

PN: Pannumériques

NOMBRES PANNUMÉRIQUES

ou PANDIGITAUX

Pangrammes numériques

Source d'amusements

Nombre formé de tous les chiffres, avec ou sans le 0.

Il en a 362 880 sans le 0 et 3 628 800 avec le 0.

Le pannumérique (direct) 123456789

Le pannumérique retourné 987654321

Un pannumérique sans 0 (nonnentien) 321456987

Un pannumérique avec 0 (décantien) 3214569870

Le plus petit avec un zéro 1023456789

Voir Écriture des chiffres

Anglais: pandigital numbers / nine digits or ten digits

Amusement

Sérotonine, prononcé à l'anglaise: zero to nine (de 0 à 9).

Sans doute la sérotonine préserve la bonne humeur de ceux qui utilisent les chiffres de 0 à 9!

Voir Pensées & humour / Sérotonine

Amuse-bouche

Un nombre pannumérique est divisible par 9

1 + 8 + 2 + 7 + 3 + 6 + 4 + 5 + 9 => 0 (preuve par neuf)

Exemple d'une opération pannumérique avec 100 pour résultat

1 + 2 + 3 + 4 + 5 + 6 + 7 + (8 x 9) = 100 >>>

Exemples d'opérations pannumériques simples:

98 765 + 1 234 = 99 999

4 x 5 = 20; 1 + 7 = 8; 9 – 6 = 3

Pannumérique double-sandwiche

181 915 267 285 296 475 384 639 743

347 936 483 574 692 582 762 519 181 >>>

Unique double-opération pannumérique:

Voir Nombre 8

Pannumérique min et max: 987 654 321 – 123 456 789 = 864 197 532

La différence est un nouveau pannumérique

987654321 = 9 + 8 x 123456789 >>>

Concaténation

918273645 = multiples de 9 concaténés

Année pannumérique

>>>

2019 = 1 + 2345 – 6x7x8 + 9

= (10 x 9 x 8 – 7 x 6 – 5) (4 – 3 + 2 x 1)

>>>

Phrase à initiales pannumériques

Un derviche tourneur qui cuisinait sans sel habitait notre demeure

Un deux trois quatre cinq six sept huit neuf dix

Carré de repunit pannumérique

1₉² = 111111111² = 1 2 3 4 5 6 7 8 9 8 7 6 5 4 3 2 1 >>>

Puissance d'un même nombre

18³ = 5 832 & 18⁴ = 104 976

69² = 4 761 & 69³ = 328 509

Racines

1 362^1/2 = 36,90528417…

2 017^1/3 = 12,63480759… >>>

Divisibilité

1 274 953 680 / 16 = 79 684 605

/ 15 = 84 996 912

Divisible par tous les nombres de 2 à 16.

Fractions (chacune pannumérique)

Entiers et fractions pour total 100 (11 possibilités)

Nombre de la Bête

666 = 1 + 2 + 3 + 4 + 567 + 89
= 123 + 456 + 78 + 9

= 21 + 543 + 6 + 87 + 9 >>>

Chanson

634-5789 Six three four five seven eight nine est un titre des Blues Brothers (Eddie Floyd et Steve Cropper). Chanté également par Wilson Pickett, Bruce Springsteen, Otis Redding, Tina Turner.

Suite en Nombre 123456789

Voir Nombres consécutifs – Index / Racine carrée des nombres pannumériques étendus

Voir autres de ce type: Nombre 11 / Tableau amusants

Unités des puissances

Les puissances 5 produisent des nombres ayant toutes les unités possibles dans l'ordre. Vrai aussi pour les puissances 5, 9, … 5 + 4k.

En présence d'une puissance cinquième, l'unité de la racine est la même:

Exemples:

12⁵ = 248 832

13⁵ = 371 293

14⁵ = 537 824

Les cubes produisent des nombres ayant toutes les unités possibles. Vrai aussi pour les puissances 7, 11, … 3 + 4k.

En présence d'un cube, si son unité est:

0, 1, 4, 5, 6, 9 le chiffre des unités est le même;

2, 3, 7, 8 le chiffre des unités est le complément à 10.

Exemples:

175 616 est le cube d'un nombre qui se termine par 6 ( 56³)

1 860 867 est le cube d'un nombre qui se termine par 3 (123³)

Les unités des puissances impaires (n¹, n³, n⁵ ...) sont celles du nombre, sauf pour les puissances n^3+4k et les unités 2, 3, 7 et 8 où elles sont en compléments à 10.

Curiosité

Égalité pannumérique exploitée pour donner une valeur pannumérique de e avec une très grande précision.

Pannumériques qui le restent par division

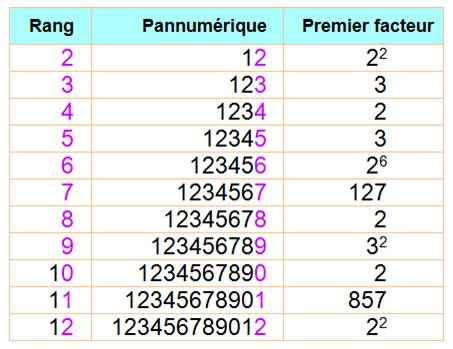
Ces six nombres pannumériques, divisés par 2, produisent des nombres pannumériques sans le 0 et, ces nombres divisés par 9 éliminent le 9.

Voir Nombre 1 037 246 958 / Pépites

QUELQUES JEUX PANNUMÉRIQUES

Opérations pannumériques

Nonentiennes

Opérations avec tous les chiffres une fois sauf le zéro

174 + 3 x 58 = 6 x 29

2 x 78 = 4 x 39 = 156

12 + 3 + 6 + 7 + 8 + 9 = 45

361, 529, 784 carrés de 19, 23 et 28

(9/12) + (7/68) + (5/34) = 1 (unique solution avec ce motif)

14368485 = 3 x 5 x 17 x 29 x 29 x 67 (deux fois les chiffres)

Les neuf produits pannumériques nonentiens

Voir Produits pannumériques

Décantiennes

Opérations avec tous les chiffres une fois avec le zéro

1 x 26 x 345 = 8970

2 x 14 x 307 = 8 596

3 x 5 694 = 17 082

7 x 4093 = 28651

40578660 = 2 x 2 x 3 x 3 x 5 x 17 x 89 x 149 (deux fois les chiffres)

9 814 072 356 = 99 066²

1 026 753 849 = 32 043²

Note:

103 = 2 + 5 + 7 + 89 tous les nombres sont premiers, mais cette configuration n'est pas pannumérique: manque le 4 et le 6.

Nom des opérations et certains exemples donnés par Louis Thépault

Voir Autres informations sur les produits pannumériques

SUITE

Fraction pannumérique

Triangle Pannumérique

Tous les chiffres une seule fois.
Somme sur les trois côtés égale 17.

			1
		6		4
	8				9
2		5		7		3

Somme Pannumérique

900 =

135

276

489

Somme pannumérique

de 3 nombres

107 + 249 = 356; 235 + 746 = 324 + 657 = 981;
134 + 586 = 720; 134 + 568 = 702; 138 + 269 = 407

Solutions de Dudeney

Deux nombres à trois chiffres qui, avec leur somme, sont pannumériques

Escalier Pannumérique

Escalier avec tous les chiffres

9	3	1
		8
		4	7	2
				5
				6

Sommes des marches et paliers = 13

Croix Pannumérique

Problème

Avec tous les chiffres

Faire la même somme sur la croix.

1				6
	2		7
		3
	8		4
9				5

Solution

3				5
	6		4
		9
	8		7
1				2

Cette solution est en plus très symétrique:

Somme 9 dans chaque branche

Soit la somme des chiffres de 1 à 9 = 5 x 9 = 45

Neuf Pannumérique

9 = 97524 / 10836
9 = 95823 / 10647
9 = 95742 / 10638
9 = 75249 / 08361
9 = 58239 / 06471
9 = 57429 / 06381

Voir Jeux

Devinette pannumérique simple

Trouvez le pannumérique ABCDEFGHI (sans le 0) tel que:

A = 2G	B = E + G	C = 2k	D > E
E = I²	F = H³ + I³	G = H + I

Solution

Carrés magiques pannumérique

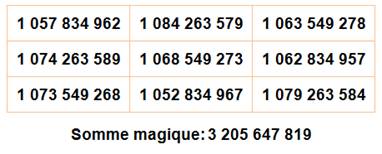
Ce carré 3x3 est magique en n'utilisant que des nombres pannumériques.

Découvert par Carlos Rivera

Ce carré 3x3 est lui aussi pannumérique, avec en plus une somme magique pannumérique.

Découvert par Carlos Rivera

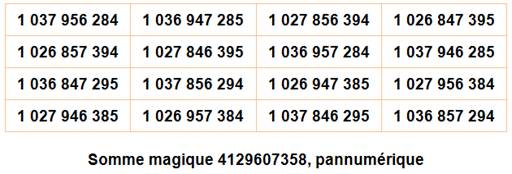
Ce carré 4x4 est pannumérique avec somme pannumérique.

Découvert par Rodolpho Kurchan

De nombreuses configurations de quatre cases donnent la somme magique dont les neufs carrés de 2x2.

Voir Autres carrés magiques pannumériques

Formule donnant les pannumériques

n N = 10ⁿ⁺¹ – 10 – 9n N / 81 N – N précédent

1 81 1 1

2 972 12 11

3 9963 123 111

4 99954 1234 1111

5 999945 12345 11111

6 9999936 123456 111111

7 99999927 1234567 1111111

8 999999918 12345678 11111111

9 9999999909 123456789 111111111

Voir Suite

Multiplications pannumériques

1	x 0,1234567890123456789 =	0,123456789 0123456789
2		0,246913578 0246913578
3		0,370370367 0370370367
4		0,493827156 0493827156
5		0,617283945 0617283945
6		0,740740734 0740740734
7		0,864197523 0864197523
8		0,987654312 0987654312
9		1,11111110 11111111101
10		1,234567890 1234567890

Lecture: 123456789 x 8 = 987654312 et en lui ajoutant 9 = 987654321

Suite >>>

Zéro?

Est-il possible d'atteindre 0 en formant une somme algébrique des chiffres de 1 à 9?

La somme simple:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

Un exemple de somme algébrique:

1 – 2 + 3 + 4 – 5 + 6 – 7 – 8 + 9 = 1

Il n'est pas possible d'obtenir une somme algébrique nulle. pourquoi?

La somme algébrique des nombres pairs donne une somme paire;

Par contre, la somme algébrique des cinq nombres impairs est un nombre impair;

Au bilan, un pair plus (ou moins) un impair donne un résultat impair.

La somme algébrique des chiffres de 1 à 9 est toujours impaire.

Voir Sommes algébriques pannumérique - Table

Pannumériques premiers ?

D'abord: tous les nombres formés avec une permutation des neuf chiffres est divisible par 9, car la somme des chiffres (45) est divisible par 9.

Divisibilité des nombres partiellement pannumériques

La majorité des nombres formés par la succession des chiffres sont composés. Le tableau donne le nombre de chiffres (rang), le nombre en soulignant que l'unité est la même que celle de son rang).

La colonne de droite montre le premier facteur. Mis à part les divisibles par 2 ou par 3, ce premier diviseur n'est pas évident. Voyez pour 7 chiffres où l'on trouve 127. En effet: 1234567 = 127 x 9721.

On trouve rapidement des facteurs monstrueux, comme celui du 27^e nombre pannumérique. Et toujours aucun nombre premier. Sur la table suivante tous les divisibles par 2 ou 3 ont été supprimés.

Suite en Pannumériques partiels

Fractions pannumériques
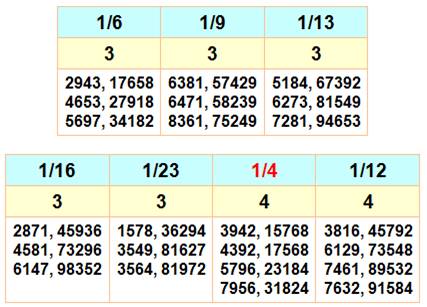
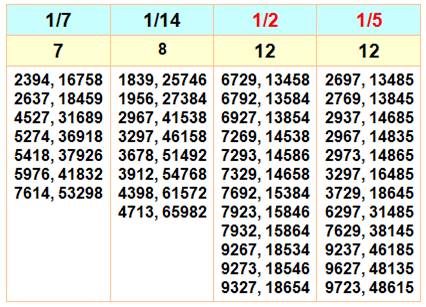
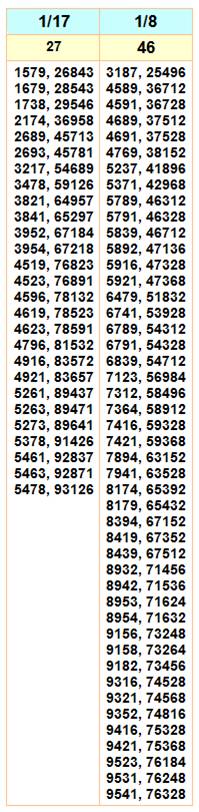
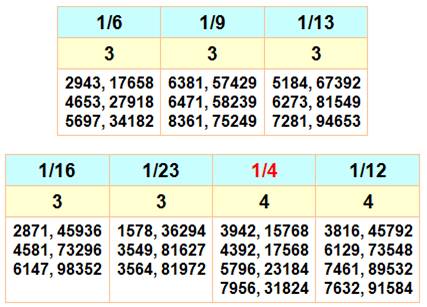
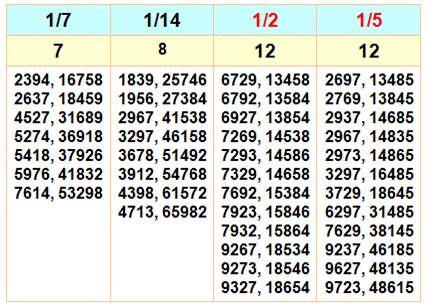
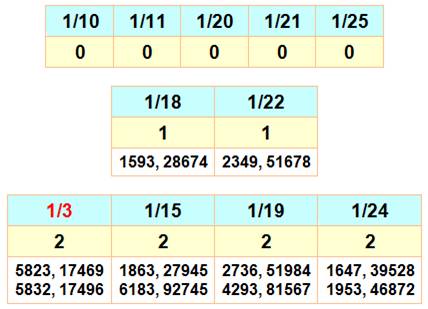
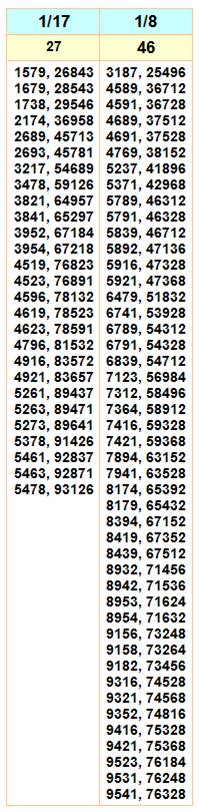
Faire une fraction réduite avec une fraction composée des neuf chiffres. Ces configurations sont plus nombreuses qu'on l'imagine. Par exemple, on compte 12 possibilités de faire la fraction 1/2. Pour les fractions de 1/2 à 1/25 On donne la fraction, la quantité de fractions et toutes les fractions si elles existent. Aucune possibilité avec 1/10 ou 1/11. Une seule fraction avec 1/18 et elle vaut: 1593 / 28674.	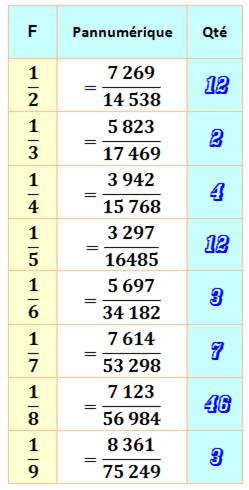Exemple pour chacune des fractions
Pour la fraction 1/2, il existe douze configurations possibles; comme avec 1/5 d'ailleurs Un record de 46 configurations est atteint avec la fraction 1/8.

Voir Jeux pannumériques

Racines pannumériques

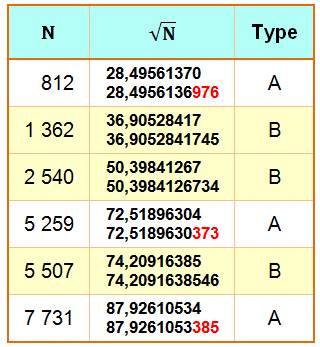
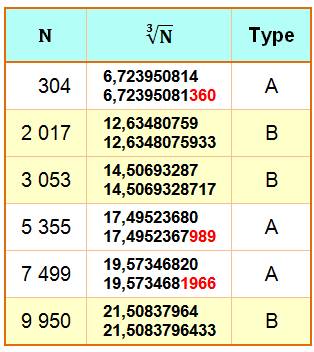
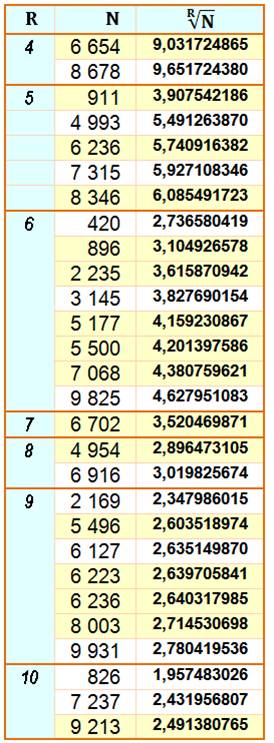
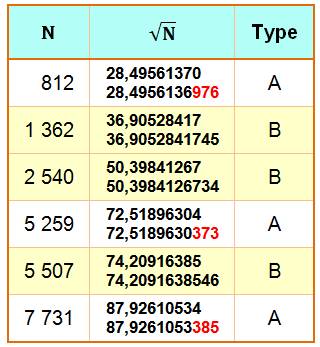
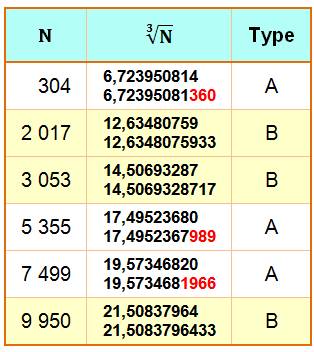
Si on prend la racine des nombres, quels sont ceux dont les dix premiers chiffres sont pannumériques? Deux races: les bons (B) avec tous les chiffres de 0 à 9 et les arrondis (A) qui ont tous les chiffres mais après avoir effectué l'arrondi.

Valeurs pour N de 1 à 10 000 et racine carrée à racine dixième (R)

Deux valeurs de la racine: arrondis à 10 décimales puis à 12 pour comparaison.

Les BONS sont notés en jaune.

Voir Nombre 2017, comme année 2017

Pannumériques en base b
Quantité en base b	Q(b) = (b – 1) (b – 1)! Exemple en base 5: 10234, 10243, … Le nombre commence par {1, 2, 3, 4}, le suivant est à choisir parmi le 0 et les trois qui restent. Soit 4 x 4 x 3 x 2 x 1 = 96. Liste: 0, 1, 4, 18, 96, 600, 4320, 35280, 322560, 3265920
Le plus petit en base b	Le plus petit nombre pannumérique en base b est de la forme: 10234… Liste: [2, 2], [3, 11], [4, 75], [5, 694], [6, 8345], [7, 123717], [8, 2177399], [9, 44317196], [10, 1023456789], [11, 26432593615], [12, 754777787027], [13, 23609224079778], [14, 802772380556705], [15, 29480883458974409], [16, 1162849439785405935], [17, 49030176097150555672], [18, 2200618769387072998445], [19, 104753196945250864004691], [20, 5271200265927977839335179]

Jeux de premiers pannumériques

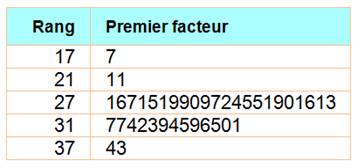
Question

Trouver un jeu de n nombres premiers formés de tous les chiffres de 1 à 9. La somme des premiers devra est la plus petite possible.

Exploration

Nombres à un chiffre: 2, 3, 5, 7.

Nombres à deux chiffres:

- unités: 1, 3, 7, 9, et

- dizaines: 4, 6, 8 obligatoirement.

Recherche de la somme

Trois nombres à deux chiffres obligatoires: en 40, 60 et 80. Soit six chiffres utilisés.

Pour minimiser la somme, on prend les trois plus petits nombres à un chiffre: 2, 3 et 5. Reste 1, 7 et 9 en unité des nombres à deux chiffres.

40, 60 et 80 en dizaines

1, 2, 3, 5, 7, 9 en unités

Leur somme:

2 + 3 + 5 + 1 + 7 + 9 + 40 + 60 + 80 = 207

Quatre solutions

Les combinaisons des dizaines et des unités, si ces nombres sont premiers (en rouge, les nombres composés) =>

Essai avec 2, 5, 7 comme unités: une seule possibilité

Somme 207

2, 3, 5, 41, 67, 89

2, 3, 5, 41, 69, 87

2, 3, 5, 47, 61, 89

2, 3, 5, 47, 69, 81

2, 3, 5, 49, 61, 87

2, 3, 5, 49, 67, 81

2, 5, 7, 41, 63, 89

2, 5, 7, 41, 69, 83

2, 5, 7, 43, 61, 89

2, 5, 7, 43, 69, 81

2, 5, 7, 49, 61, 83

2, 5, 7, 49, 63, 81

Sommes suivantes (exemples)

2, 5, 11, 43, 67, 89 => 217

2, 5, 13, 41, 67, 89 => 217

2, 5, 13, 47, 61, 89 => 217

2, 5, 17, 43, 61, 89 => 217

2, 5, 13, 43, 67, 89 => 219

2, 5, 13, 47, 67, 89 => 223

2, 5, 17, 43, 67, 89 => 223

Note: avec seulement 8 chiffres au lieu de 9

2, 3, 5, 7, 41, 89 – le 6 manque

2, 3, 5, 7, 61, 89 – le 4 manque

Devinette pannumérique – Solution

Énigme

Trouvez le pannumérique ABCDEFGHI (sans le 0) tel que:

A = 2G	B = E + G	C = 2k	D > E
E = I²	F = H³ + I³	G = H + I

Solution

	A	B	C	D	E	F	G	H	I
E = I²				D>E	4				2
F = H³ + I³					4	9		1	2
G = H + I					4	9	3	1	2
A = 2G	6				4	9	3	1	2
C = 2k	6		8		4	9	3	1	2
B = E + G	6	7	8	5	4	9	3	1	2

Retour

Énigme citée dans: Méga – 600 jeux et énigmes – Éric Berger, Pascal Guichard, Michèle Lecreux et Clémence Roux de Luze

– Hors Collection – 2012

Suite	Voir haut de page Carré magique 3x3 Carrés, cubes et puissances pannumériques Cent en somme pannumérique Cent et autres pannumériques – Index Croix numérique Diviseur: tous les chiffres dans les diviseurs Divisibilité par 11 des pannumérqiues Divisions des pannumériques et des retournés Exp(1) = e en pannumérique Grille des chiffres de 1 à 8 – Énigme Multiplications pannumériques (pdf) Nombres carrés et pannumériques Nombres pairs dans une liste pannumérique Nombre 123456789 Nombre 123 456 789 x 9 = 1 111 111 101 Pannumériques divisibles par 9 Pannumériques divisibles par 11 Puissances de 2 pannumériques Pi pannumérique Puzzle pannumérique vietnamien Sommes 3 3 3 pannumériques Sommes de premiers pannumériques Valeur de e avec les neuf chiffres Plus petite puissances pannumériques des nombres
Voir	Nombre phénix ou de Lewis Carroll Nombre magique 142857
Aussi	Anagramme de chiffres Carré des nombre en 11, 101 … Carré latin pannumérique Chiffres en miroir Croix pannumérique Jeux – Index Nombre têtu Nombres consécutifs	Nombres zèbre Rep-Digit Rep-Unit Somme de 1 à 100 Sommes dans figures Sommes pannumériques premières Triangle magique pannumérique
DicoNombre	0,5 en chiffres 100 en chiffres 1000 en chiffres Carré et cube pannumériques Carré pannumérique Carrés pannumériques	Curiosité avec 1234… Nombre 207 Sommes des consécutifs Soustraction pannumérique Suite 0,1234.... Suite 1234...
Sites	Voir le site complet sur ce sujet de Patrick De Geest The Nine Digits Most Recent Page with some Ten Digits (pandigital) exceptions Magic squares and pandigital numbers – Carlos Rivera Nine to One – Maths Puzzle Mall OEIS A050278 – Pandigital numbers: numbers containing the digits 0-9.
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Formes/PanNum.htm

Renvois de liens

Nombre 123 456 789 >>>

Analyse des pannumériques >>>

Curiosités avec 123456789 >>>

CERCLE >>>

102345698 7 896543201 >>>