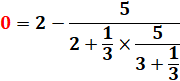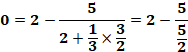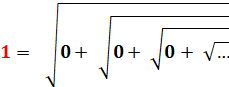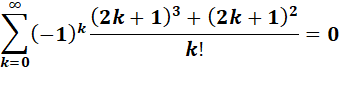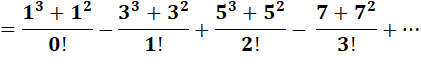nombre zéro en arithmétique

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/03/2025 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES					Glossaire Nombres
Infini Nombres décimaux <1	0 Zéro – Nul – Rien - Vide					Un 5 10 Autres
Le 0 pour débutant			Carte identité		Nom des nombres
Le ZÉRO		Concept 0	Arithmétique 0	Sciences 0	Expressions en 0
Histoire 0		Culture 0	Algèbre 0	Abeille et 0	Proverbes avec 0
Zéro en quiz		Divers 0	Infini & zéro	Somme nulle	Jeux & Curiosités 0
			Sommaire de cette page >>> Zéro en arithmétique >>> Identités avec zéro – Curiosités >>> Élément neutre >>> Nombres premiers >>> La formule en ZÉRO de Ramanujan >>> Paradoxe du triangle rectangle

C'est vrai! Cette année, j'ai décidé de m'octroyer une augmentation de zéro sur mon salaire.

Dessin de Randy Glasbergen - 2001

Les hommes sont comme les chiffres: il n'y a rien de plus fort qu'un zéro bien placé.

Voir Pensées & humour

Le nombre ZÉRO

Le zéro est défini comme la taille (cardinal) de l'ensemble vide.

Dans un paquet de bonbons vide, il y a 0 bonbon.

C'est aussi le plus petit nombre entier naturel (ensemble N) à ne pas avoir de prédécesseur.

0 + 0 + 0 + … = 0

0 x 0 x 0 x … = 0

Il est unique qu'un produit infini soit égal à la somme infinie.

Le nombre zéro est à l'origine des nombres >>>.

Les nombres au voisinage de zéro sont les infinitésimaux >>>.

Devinette

Calculez le produit suivant: les doigts de la main gauche de tous les humains par les doigts de la main droite. Comment évolue ce produit en fonction de la population mondiale?

Solution

Arithmétique

Avec zéro, au mieux on reste sur place (+0) et au pire on retombe à zéro (x0).
Avec un, au pire on reste sur place (x1) et au mieux on avance d'un cran (+1).

0: élément neutre de l'addition et de la soustraction:

X + 0 = X

0: élément absorbant de la multiplication, mais interdit pour la division !

X . 0 = 0

Opérations classiques

Addition	x + 0	=	x
Soustraction	x – 0	=	x
Multiplication	x. 0	=	0
Division	0 / x	=	0 pour x 0
	x / 0		Indéfini
	x / (a – b)		Indéfini, si a = b
	0 / 0 5x / x	=	Indéterminé 5 par exemple

Autres opérations

Factorielle	0 !	=	1 >>>
Puissance	10 ⁰	=	1
	a ⁰	=	1 >>>
	0 ⁿ	=	0
	0 ^1/n	=	0
	0 ⁰	=	Indéterminé entre 0 et 1 et par définition = 1
	n / 0	=	impossible
Logarithme	Log _b 1	=	0
Ensemble	Card()	=	0 (définition)

PPCM

PGCD	(0, n)	=	n
	(0, 0)	=	indéfini
PPCM	(0, n)	=	0 est le PPCM de tous les entiers

Le zéro qui donne 1

Comment montrer logiquement que 2⁰ = 1, comme a⁰ = 1

Comment montrer logiquement que 0! = 1

Quelques identités avec zéro (curiosités)

0 = 12 – 34 + 56 – 78	Jeu avec les huit premiers chiffres.
0 = !1 = 1! (1 – 1 / 1!)	Sous-factorielle de 1.
Explications	Une formulation par fractions à étages parmi d'autres possibles.
	Formulation pannumérique de zéro
0 = 2 – (2 x 2/2) 6 = (0! + 0! + 0!)!	Faire zéro avec 4 deux. Faire six avec 3 zéros. Voir Fameux défi des quatre 4
	Faire quelque chose avec 0, faut le faire ! Voir Racines continues
0 = 1 + j + j²	La somme des racines cubiques de 1 est nulle.
0 = 144⁵ – 133⁵ – 110⁵ – 84⁵ – 27⁵		Somme de puissances 5. Voir Nombre 144

10 007

100 000 007

Plus petit premier à zéros.

Plus petit à sept zéros.

ENSEMBLE – Élément neutre

x + e = e

x + 0 = 0

Zéro est l'élément neutre d'un groupe muni d'une loi additive.

Il s'agit d'une généralisation du cas classique du 0 avec les nombres et l'addition.

Zero is the identity element in an additive group or the additive identity of a ring.

NOMBRES PREMIERS

Le pourcentage de nombres premiers par rapport aux nombres entiers est nul. Autrement-dit: la quantité de nombres premiers est de plus en plus faible pour les grands nombres.

Pourtant la quantité de nombres premiers est infinie.

Lorsque j'avais vingt ans, je n'étais pas un homme, j'étais un étudiant. Les vingt ans aujourd'hui n'ont pas la même qualité, la même chair numérique. L'arithmétique elle aussi est foutue. Je n'ai jamais compris pourquoi les zéros font des nombres.

Malek Haddad (1960)

Voir Pensées & humour

La formule en ZÉRO de Ramanujan

Somme alternée des cubes plus les carrés des nombres impairs divisé par une factorielle formulée par Ramanujan.

Tableau des premières valeurs

À zéro franc près, nous obtenons le même résultat que vous.

Bêtisier des impôts

Voir Pensées & humour

Paradoxe du triangle rectangle

Question

Je trace un triangle rectangle sur un papier quadrillé. Quelle que soit la taille du quadrillage quand je vais d'une extrémité à l'autre de l'hypoténuse en suivant les carrés, je parcours toujours la distance égale à la racine de la somme des carrés des deux côtés de l'angle droit.

Comment se fait-il que, si les carrés étaient infiniment petits, je parcourrais toujours la distance donnée par Pythagore plus grande que celle des côtés?

Réponse

Il faut noter que la relation dans le triangle rectangle est bien a² + b² = c²

Imaginez le triangle rectangle et dessinez un carré (géométrique) sur chacun des côtés. L'aire de chacun de ses carrés est: a², b² et c². Voir le dessin.

La relation de Pythagore dit que le carré sur c est plus grand que chacun des deux autres (a et b). Son aire (c²) est même la somme des deux aires (a² + b²).

Si le triangle rectangle devient de plus en plus petit, les longueurs des côtés tendent vers 0 et de même l'aire des carrés.

C'est là me semble-t-il qu'il y a une interrogation légitime.

Eh bien, la solution c'est qu'il n'y a pas plusieurs types de 0.

Si a et b tendent vers 0, alors a² et b² tendent vers 0 et c² (qui vaut a² + b²) tend vers 0 + 0 = 0 et c, sa racine carrée, tend vers 0.

C'est un peu paradoxal lorsqu'on imagine la géométrie, mais cela devient logique en imaginant les nombres (0 + 0 = 0).

Une chose à ne pas oublier: en géométrie une droite a une longueur mais pas d'épaisseur (contrairement à la ligne dessinée au crayon). Un point n'a ni longueur ni épaisseur.

Voir Paradoxes de l'infini

Merci à Thierry P. pour cette question

Devinette – Solution

Question

Calculez le produit suivant: les doigts de la main gauche de tous les humains par les doigts de la main droite. Comment évolue ce produit en fonction de la population mondiale?

Réponse

L'auteur de cette énigme compte sur le fait qu'il existe dans le monde au moins une personne qui n'a pas de doigts. Ce qui conduit à un produit nul.

Retour

Suite	Sciences du zéro Voir en haut de page Les tracas du débutant
Voir	Abeille et la quantité 0 Calcul mental – Index Infinitésimaux Magie Nombre d'Or Petits nombres Un Zéro et infini
Site	Comment multiplier rien du tout ? – Micmaths - Mickaël Launay – Vidéo
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/ZerArith.htm