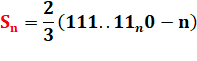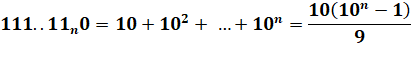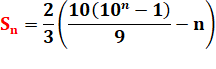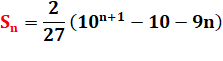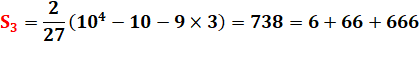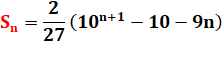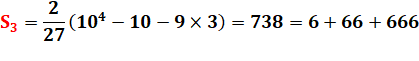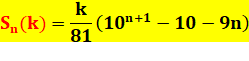|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
NOMBRES
UNIFORMES ou REPDIGITS Nombres dont les chiffres sont
répétés, comme 3333 ou 555 … Les nombres avec des 1 (repunits) sont ceux
comme 11, 111, 1111 … On
dit: nombres uniformes de la classe Uk,
comme par exemple 44 est un nombre uniforme de la classe U4. Tous ces nombres sont palindromes
et multiples d'un repunit. Le nombre de la Bête (666) est un repdigit Un des intérêts (amusement) est de rechercher les premiers parmi de tels nombres. Mot-valise
formé avec répétition des digits (chiffres). |
Anglais: Rep-digit or Repdigit or Monodigit
Une
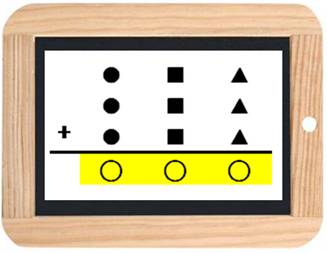
multiplication esthétique produisant un repdigit
|
|
Voir
Multiplications
en puzzle
|
Question Quelles sont les solutions de cette opération ?
Il existe deux solutions (148 et 185) pour
lesquelles le chiffre ◯ est égal à l'un
des chiffres du nombre. Généralisation Il existe dix solutions avec ◯ égal un chiffre quelconque et avec deux, trois, … opérandes dans la
somme. Certaines sont triviales comme 2 × 222 = 444. |
Deux solutions originales
Dix solutions
|
|
|
Avec des nombres à deux
chiffres, les seuls cas non triviaux est: |
Avec des nombres à quatre
chiffres, aucun cas non trivial. Exemple de cas trivial: 3 × 3 333 = 9 999 |
|
Voir Brève 52- 1036
|
|
|||
|
Nombre formé par la répétition du seul et même chiffre (digit en
anglais).
Un nombre uniforme est noté en donnant deux des
chiffres accompagnés d'un indice indiquant la quantité de chiffres répétés (à
ne pas confondre avec l'indice indiquant une base de numération. |
Exemples 1111 33333333333333333 9999 Filiation Tout repdigit est un multiple d'un repunit. 333 = 111 x 3 555 = 111 x 5 Notation 111
= 113 |
||
|
Numération |
Ex: [555]3 = 5 (3² + 3 + 1) = 65 en décimal. Voir Identité remarquable / nombres brésiliens |
||
|
|
||
|
|
Commentaire Procédure nommé Rep qui répond OK = 1 si le
nombre n est un repdigit et 0 sinon. Le nombre n est converti en une liste N (effet de
sa conversion en base 10). On compte la quantité de chiffres en q. Boucle qui compare chaque chiffre au suivant et
qui place le témoin OK à 0 s'ils sont différents. Après cette moulinette, si OK = 1, c'est que le
nombre n est un repdigit. La procédure retourne la valeur de la variable
OK. |
|
Voir Programmation – Index
|
|
||
|
Exemple
|
Exemples 111 = 1x102 + 1x10 + 1 222 = 2x102 + 2x10 + 2 kkk = kx102 + kx10 + k Forme
générique classique Un,k
= k x 11n
= k (10n + 10n-1 +…+ 10 + 1) Notation U1,3 = 111 U5,6 = 555 555 Forme
générique en base B
En
base 10
|
|
La somme des entiers est un repdigit ?
|
Devinette Quels
sont les nombres repdigits à trois chiffres qui sont sommes des entiers de 1 à
n ? Réponse La
somme des
entiers de 1 à n est repdigit à
trois chiffres si:
Un
test sur (222, 444, 666, 888) montre que seul 666 est la réponse. Alors k = 3
et n = 36, car 36 x 37 = 1332 et 1332 / 2 = 666. |
|
|
||
|
Voir Démonstration
|
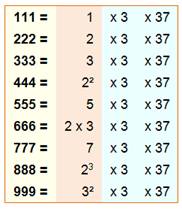
3333 = 1111 x 3 5555 = 1111 x 5
111 = 3 x 37 111 111 = 3 x 37 037 =
3 x 37 x 1001 111 111 111 =
3 x 37 037 037 =
3 x 37 x 1001 001 555 = 5 x 3 x 37 11 est premier Le suivant est 1119 |
|
|
Avec
un seul trait, rectifier cette opération
Un
malin préconisait de barrer le signe égal. Il faut trouver autre chose. |
|
|
|||||||||||||||||||||
|
Montrez qu'un
repdigit comprenant 3n
chiffres est divisible par 3n |
Démonstration par induction. |
||||||||||||||||||||
|
C'est vrai. Voir Divisibilité
par 3 |
31 = 3 m = aaa La somme des chiffres est égale à 3a m est divisible par 3. |
||||||||||||||||||||
|
L'est-elle pour k + 1? |
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
m' = m (100…0 + 100…0 + 1) = ( 3k A) ( 3 B) = 3k+1 C |
||||||||||||||||||||
|
|
3k+1 |
||||||||||||||||||||
|
Exemples |
|
||||||||||||||||||||
Voir Divisibilité
des formes polynomiales
|
|
|
|
Exemples 1 / 7 => 142857 x 7 = 999 999 = 96 1 / 17 => 588 235 294 117 647 x 17 = 916 1 / 19 => 52 631 578 947 368 421 x 19 = 918 Rappel 0, 999 … = 1 >>> |
|
Voir suite en Repdigit en 999 …
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Motifs
Règle
générale
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
D'une
manière générale n² = (10k + k)² = 11² k² = 121 k² 22² = 121 x 4 = 484 Le carré d'un repdigit à deux chiffres est divisible
par 121. n² = (100k + 10k + k)² = 111² k² = 12321 k² n² = (…)² = 11…1k² k² Le carré d'un
repdigit d'ordre k est égal au produit du carré de son
repunit associé par k². Carré
des repdigits en 9
De sorte que, par exemple, 999² = 998 001 Avec cette coquetterie: 999 = 998 + 001, valable pout tous
les repdigits en 9. 999
999² = 999 998 000 001 Formule
magique de calcul mental
Pour élever au carré un nombre en 99…99, il suffit de concaténer deux
nombres simples: 99… 98 et 00..01. Principe
général Repdigit aa…ak et b = 10 – b Son carré (aa…ak)² = 102k – 2b
x10k + 1 Table
des carrés des repdigits >>> |
|
|
Seuls
carrés sommes de deux repdigits:
121
= 11² = 22 + 99
= 33 + 88 = 44 + 77 = 55 + 66
144
= 12² = 33
+ 111
1
444 = 38² = 1 111 + 333 44 521
= 211² = 44
444 + 77 |
Voir Repdigit égal somme de carrés
|
|
|
|
Curiosité Facteurs: 999 999 = 1 x 33 x 7 x 11
x13 x 37 Arrangeons: 999 999 = 7 x 11 x13 x 27
x37 Sur le tableau suivant, F est le facteur, 1/F son
inverse, P4 le produit des quatre autres facteurs et 1/P l'inverse de ce
produit. Notez comment chacun est lié aux quatre autres.
Pas si extraordinaire… prenons 7:
Ce calcul montre que nous retombons sur nos pieds. |
|
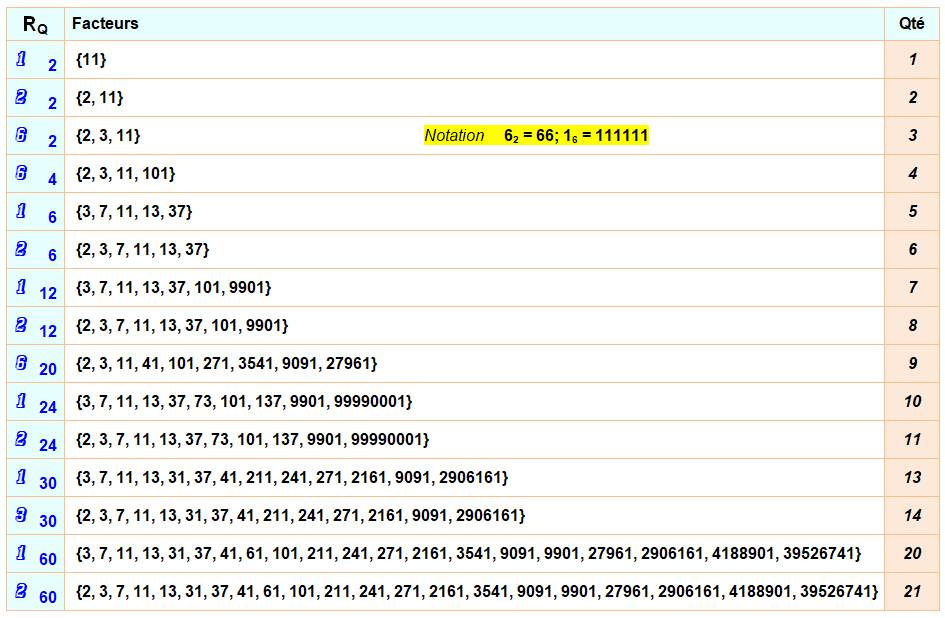
Record de factorisation sans puissance des repdigits
Exemple: 6666
= 2 x 3 x 11 x 101. Ce nombre est le plus petit repdigit à quatre facteurs sans
exposant
Record de
factorisation des repdigits – Facteurs avec exposants
Exemple: 3, 8 => 888 = 23 x 3 x 37.
Ce nombre est le plus petit repdigit à cinq facteurs avec exposants
|
|
|||
33…3n
est composé de n fois le chiffre 3 Voir démonstration |
|||
|
|
|
|
Nombres
premiers s'écrivant avec deux chiffres, l'un puis l'autre.
Nombres
premiers s'écrivant avec même chiffre en tête et en queue
|
|
|
|
|||
|
Il faut
calculer la somme de ces repdigits en 6 jusqu'au énième (n > 1). |
|
||
|
Calculs |
|
||
|
Résolution |
|
||
|
Mise en évidence de 9 |
|
||
|
Calcul du repunit |
|
||
|
Retour à Sn |
|
||
|
Finalement |
|
||
|
Exemple |
|
||
|
Généralisation pour les repdigits en k |
|
||
|
Exemple k = 3 |
|
||
|
Tableau des valeurs k + kk + kkk + … Lignes pour n = quantité de termes de la somme Colonnes pour k, le type de repdigit. Exemple de lecture 6 + 66 + 666 + … + 6666 666 666 = 7 407 407 400 Notez la régularité
des motifs, notamment avec 9: 11100010a avec a = 10 – n. |
|
||
Voir Page duale
|
|
|||
|
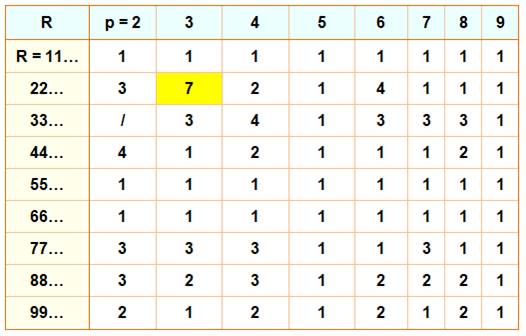
Les repdigits R à la
puissance p ne comporte jamais les chiffres indiqués dans la zone rose. Exemple 333…3 n'a pas les chiffres (1, 4 et 8) 333 = 35 937 3333 = 36 926 037 33333 = 37 025 927 037 etc. Tableau testé jusqu'à mille chiffres dans chaque repdigit. |
|
||
|
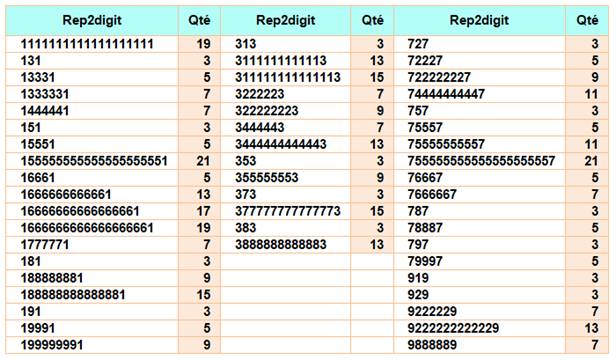
Quel est le premier
k-repdigit dont la puissance p comporte le chiffre k pour la première fois ? Record pour 222 2223 = 10 973 903 978 085 048 2 222 2223 = 10 973 933 607 682
085 048 avec sept fois le chiffre"2". |
|
||
|
|
|
Suite |
|
||
|
Voir |
|
|
|
|
DicoNombre |
|
|
|
|
Sites |
|
||
|
Cette page |
|||
