NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/05/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Bases et amusements			Glossaire Carrés magiques
INDEX Carrés magiques Ordres Constructions Magie Jeux de grilles Jeux et énigmes	Latin	Gréco-latin	Avec 0 à 9	Vers Magiques
	Multi-magiques	Jeux (à trous)	Décimal	Sudoku
		Premier	Pannum. premier	Inverse premiers
		Sommaire de cette page >>> Avec 1 / 7: semi-magique >>> Avec 1 / 19: magique

CARRÉS MAGIQUES avec les décimales

de l'inverse des nombres PREMIERS

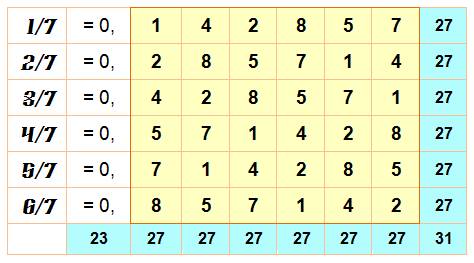
La propriété de permutation des multiples de 1 / 7 offre la possibilité de construire une carré magique ou pas. Vérifions!

Note: une autre propriété toujours amusante: chaque chiffre d'une moitié ajouté à son homologue de l'autre moitié donne 9: 1+8 = 9, 4+5 = 9 et 2+7 = 9.

Anglais: Prime reciprocal magic square

Avec 1 /7 – Semi-magique
Dans le cadre jaune, les six premiers multiples de 1 / 7 en ne conservant que la chiffres répétitifs. Il s'agit d'un carré 6 x 6. Dans la mesure ou ce sont les mêmes chiffres qui sont permutés, il est normal de trouver un carré semi-magique: sommes sur les lignes = sommes sur les colonnes. Par contre, pas de chance les diagonales ne marchent pas. La moyenne est bien 27 (23 + 31 = 54). Le carré n'est pas pleinement magique.

Voir Propriétés magiques de 142 857

Avec 1 / 19 – Un carré magique rare!
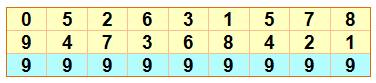
Cette fois les diagonales somment en 81 comme les lignes et les colonnes. Ce carré 18 x 18 est pleinement magique. Cependant non orthodoxe dans la mesure où ce ne sont pas les nombres successifs qui remplissent les cases Il est toutefois pannumérique, car tous les chiffres de 0 à 9 sont présents. Notez toujours que chaque moitié est le complément à 9 de l'autre:

Bilan

Le carré avec 1/19 est bien magique, mais c'est un des rares connus en base 10. Ils sont très nombreux en diversifiant la base.

Par exemple 1 / 53 en base 12.

Ou encore 1 / 223 = 1 / 22021₃ = 0,0000100210210102121211101202221112202… dont la somme est 222.

Suite	Nombres premiers – Introduction Nombres premiers – Index Magie avec des figures géométriques
Voir	Bi, tripartitions Géométrie Glossaire pour s'y retrouver Humour Jeux Morceaux choisis Nombres magiques SOS- Débutants Théorie des Nombres
Sites	Liens vers les sites carrés magiques Carré magique d'inverses de nombres premiers – Wikipédia avec liste des carrés selon la base utilisée
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMInvers.htm