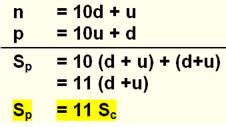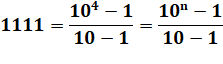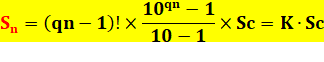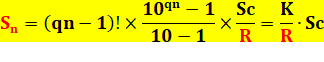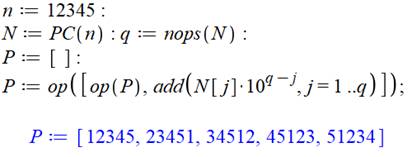|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres permutés Nombres
obtenus par permutation des chiffres d'un nombre, par échange des chiffres
les uns avec les autres. Somme des permutés en bref
|
|
|
||
|
Permutations quelconques Ce sont tous les nombres obtenus par échanges des
chiffres les uns par les autres. Exemples 123456789 un nombre. 987654321 une forme permutée de ce nombre. 213456789 une autre forme permutée. Permutations circulaires Dans une permutation circulaire, les chiffres sont
tous décalés vers la droite (ou vers la gauche). Exemples 123456789 un nombre. 234567891 une permutation circulaire de ce nombre. 345678912 une autre permutation. Le nom vient du fait que si l'on imaginait les objets disposés en
cercle, la permutation circulaire consisterait simplement à faire tourner le
cercle sur lui-même. |
|
|
|
|
||
|
Avec deux chiffres distincts, il n'existe que deux
possibilités. Échange des unités et des
dizaines. |
23 32 Les deux permutations de 23. q = 2 chiffres; P = 2 permutations |
|
|
Avec trois chiffres distincts, comptons les
permutations (avec n = 234)
|
234 243 324 342 423 432 Les six permutations de 234. q = 3 chiffres; P = 6 permutations |
|
|
Ou encore: P = 4 x 3 x 2 Ce qui fait: P = 4! |
Les 24 permutations de 1234. q = 4 chiffres; P = 24 permutations |
|
|
|
Les P permutations de n. Avec
q chiffres distincts; P = q! permutations |
|
|
|
Exemple Avec 111223, on a: 6! = 720 permutations dont 3! x 2! = 12
fois redondantes soit: 720 / 12 = 60
permutations pures. Voir le
cas de Mississippi pour explications. |
|
|
permutés
circulairement |
|
||
|
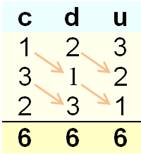
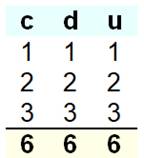
Cas d'un nombre à trois chiffres: Par définition, un chiffre occupera successivement
chacune des positions dans le nombre. De même chaque position
du nombre verra défiler chacun des chiffres du nombre. |
La somme dans chaque colonne est égale à la somme des chiffres. Spcircul.
= 111 Schiffres Voir Nombre 666 |
||
|
Généralisation à un nombre n de q
chiffres. Notez que
K est fonction de la quantité de chiffre et non de la nature des chiffres |
Spcircul.
= 11…1q fois Schiffres
Exemple avec 1234 1234 + 2341 +
3412 + 4123 = 1 111 x 10 = 11
110 Exemple avec 3456 3456 + 4563 +
5634 + 6345 = 1 111 x 18 = 19
998 |
||
|
Exemples Somme des permutations circulaires des nombres
successifs en 123 … 1234 + 2341 + 3412 + 4123 = 11110 |
1, 1 12, 33 123, 666 1234,
11110 12345,
166665 123456,
2333331 1234567,
31111108 12345678,
399999996 123456789,
4999999995 |
||
|
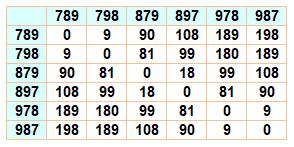
Nombres SPC Nombres égaux à la somme de tous les
nombres obtenus par permutation circulaire des chiffres. Plusieurs nombres
permutés sont possibles comme le montre le tableau. Exemple 176 = 79 + 97 = 88 + 88 = 97 + 79 Observation La somme des chiffres de chaque
nombre à permuter est constante (16 pour l'exemple ci-dessus). |
|
|
|
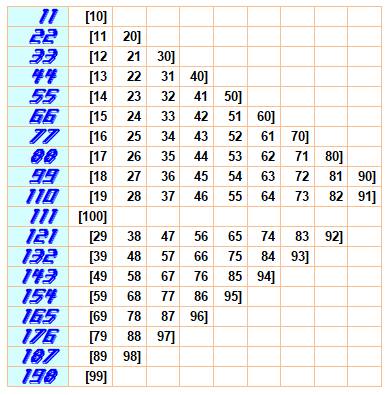
De 100 à 1000, on
rencontre les nombres en 100 ci-dessus et les seuls repdigits à trois chiffres
ci-contre. (Le successeur de 198 est 222). |
|
|
|
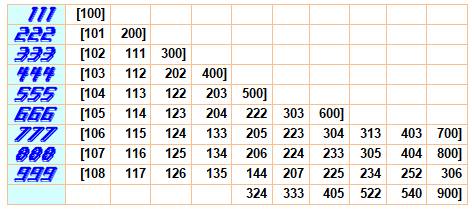
Avec quatre chiffres, les nombres à
permuter sont ceux dont la somme des chiffres à pour unité l'unité des
nombres. Exemple:
1110, [109, 118, 127, 136, 145,…] 1998, [189, 279, 288, 369,
378, …] |
Avec quatre chiffres,
on a: |
|
Voir Programmation des permutations
circulaires / Nombre sommes de
retournés / Nombre NRC
|
|
|||
|
Nous allons monter que la somme de tous les
nombres permutés ne dépend que de la somme des chiffres du nombre. |
Spermutations = k . Schiffres Hypothèse:
les chiffres sont tous distincts. Sinon les
permutations sont moins pertinentes. |
||
|
2 chiffres Ex: 23 + 32 = 55 = 11 x 5 Un nombre de deux chiffres ajouté à son retourné
est divisible par 11. |
|
||
|
3 chiffres Ex: 234+243+324+342+423+432 = 1998 = 222 x 9 Voir Divisibilité
par 222 |
|
||
|
4 chiffres Ex: 1234 + 1243+ … + 4321 = 66 660 = 6 666 x 10 Remarquez que le 6 qui intervient est le 6 de 3! |
Sp = 6
000 Sc + 600 Sc + 60 Sc + 6 Sc Sp = 6 666 Sc |
||
|
5 chiffres Ex: 12345 + 12354+ … + 54321 = 266 664 x 15 = 3 999 960 |
Calcul du coefficient avec 4! = 24
Sp = 266 664 Sc |
||
|
6 chiffres avec 5! =
120 |
Sp = 13 333 320 Sc |
||
|
Nombres de 100 à 1000,
sommes de toutes les permutations des chiffres d'un nombre Exemple = 114 +
141 + 411 = 33 + 303 + 330 = 6 + 60 + 600 |
110, [19,
28, 37, 46, 64, 73, 82, 91] 111, [100,
111] 121, [29,
38, 47, 56, 65, 74, 83, 92] 132, [39,
48, 57, 75, 84, 93] 143, [49, 58,
67, 76, 85, 94] 154, [59,
68, 86, 95] 165, [69,
78, 87, 96] 176, [79,
97] 187, [89,
98] 222, [101,
200, 222] 333, [300,
333] 444, [112,
202, 400, 444] 555, [113,
122, 500, 555] 666, [102,
114, 303, 600, 666] 777, [115,
133, 223, 700, 777] 888, [103,
116, 224, 233, 404, 800, 888] 999, [117,
144, 225, 900, 999] |
||
|
Les suivants |
Liste 1110,
1221, 1332, 1443, 1554, 1665, 1775, 1887, 1998, 2109, 2220, 2222, 2331, 2442,
2553, 2664, 2775, 2886, 3108… Exemple 1998, [108,
126, 135, 207, 234, 288, 306, 405, 477, 558, 909, 990] |
||
|
|
|||
|
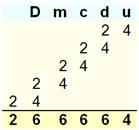
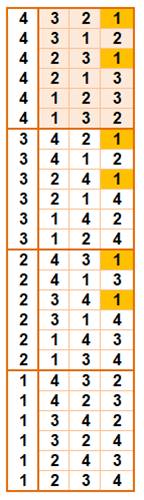
Calcul direct Chaque
colonne du tableau comporte les mêmes chiffres, mais pas dans le même ordre. De sorte
que la somme de tous les nombres permutés est égale à la somme de chacun des chiffres
d'une colonne, pondérée par la puissance de 10 qui correspond à la position
de la colonne. En
considérant la colonne de gauche, la quantité de lignes répétitives est égale
à (n – 1)! Pour l'exemple: n = 4, ce qui donne: 3! = 6
lignes dans chacun des quatre blocs; chaque bloc contenant un chiffre
différent en colonne de gauche. La somme
du tableau en exemple est égale à:
Le nombre
en jaune est un repunit
à quatre chiffres qui s'écrit aussi:
Soit la
formule générale :
qn = quantité de chiffres dans n et Sc = la somme des chiffres de n. |
Les 24 permutations du nombre 4321
Somme de toutes
ces permutations: 66 660 |
||
|
Cas de la répétition de chiffres Dans ce
cas la quantité de permutations est divisée par un coefficient de répétions R
(élimination de permutations identiques). Si le chiffre
C est répété c fois, il faut diviser par c! (Voir comment ces répétions sont traitées avec le
cas de Mississippi) Avec R = c1! x c2! … la formule
devient:
|
Exemple Avec 111223, on a: 6! = 720 permutations dont 3! x 2! = 12
fois redondantes soit: 720 / 12 = 60
permutations pures S = 120 x 111111 x 10 / 12 S = 11 111 100 Avec 122333444 S = 41 999 999 995 800 |
||
|
Coefficient multiplicateur K Ce
coefficient est indépendant des chiffres du nombre. Il est caractéristique de
la quantité n de chiffres. Exemple avec 123 456 789 ou tous
les nombres formés avec ces neuf chiffres K9 = 4 479 999 995 520 Sc = 9 x 10 / 2 = 45 S = 201 599 999 798 400 Formule de récurrence
Exemple
|
n,
K 1, 1 2, 11 3, 222 4, 6666 5, 266664 6, 13333320 7, 799999920 8, 55999999440 9, 4479999995520 10, 403199999959680 11, 40319999999596800 12, 4435199999995564800 13, 532223999999946777600 14, 69189119999999308108800 15,
9686476799999990313523200 16,
1452971519999999854702848000 17, 232475443199999997675245568000 18,
39520825343999999960479174656000 19,
7113748561919999999288625143808000 20,
1351612226764799999986483877732352000 |
||
Merci à Alain
Rodot pour l'idée de cette formulation
|
|
||
|
|
Commentaires Calcul de la somme des permutés d'un nombres en tenant compte de la
répétitions des chiffres. Calcul systématique Introduction manuelle du nombre. Conversion en base 10 pour disposer des chiffres. Toutes les permutations des chiffres en P. Reconstitution des nombres permutés à partir des chiffres en exécutant
la boucle en i Addition de tous ces nombres en S. Calcul avec la formule Introduction manuelle du coefficient de redondance (ici 2 fois le
"2" et deux fois le "3", soit R = 2! x 2! = 4. Voir
comment compter
automatiquement) Calcul de la somme des chiffres en Sc (1+2+2+3+3) = 11. Calcul de la formule. En bleu les résultats du traitement. Note: la première partie du
programme a un but de vérification. Si on voulait traiter de grands nombres,
il faudrait passer aux matrices au
lieu de la liste. |
|
Voir Programmation – Index
![]()
|
|
||
|
La différence de
deux nombres permutés est un multiple de 9. Encore un effet
de la preuve
par neuf ou plus exactement de la congruence mod 9 Chaque nombre
permuté a la même congruence mod 9 et
la différence est donc nulle |
N – Nperm = 9k
|
|
Voir Cycle de Kaprekar
|
|
|||
|
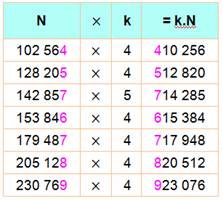
Prendre un nombre, le multiplier et retrouver le
nombre initial permuté d'un cran: le chiffre de queue (unité) se retrouve en tête. Tableau: les sept telles opérations
jusqu'à N = 1 milliard et k de 2 à 9. K = 4 ou 5. Rien avec les autres chiffres. |
|
||
|
Le
plus petit tel nombre avec k = 9 pour 1,011… 1043
10112359550561797752808988764044943820224719
x 9 = 91011235955056179775280898876404494382022471 |
|||
|
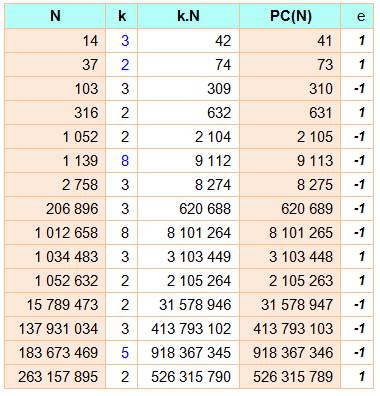
Si l'on admet un écart de 1 pour le nombre
permuté, on obtient le tableau ci-contre jusqu'à N = 1 milliard et k de 2 à
9. Exemple 14 x 3 = 42 PC(14) = 41 Écart: e =
1 |
|
||
![]()
|
|
|||
|
|
Commentaires Appel des logiciels de combinatoire et de manipulation des
listes. Lancement d'une procédure de recherche des
permutations circulaires (PC). Liste
des chiffres de n dans N: 1) en convertissant
n en base 10 qui énumère les chiffres dans l'ordre inverse; et, 2) en
renversant la liste pour obtenir les chiffres dans l'ordre du nombre. La quantité de chiffres est identifiée dans q. Ouverture d'une liste P qui recevra les
permutations circulaires. Une première boucle explore les q permutations du
nombre n, chacune étant placée en PP. La seconde boucle calcule la permutation en
déplaçant circulairement chacun des chiffres. Note: N [ (i + j) mod q +
1]: La liste P des permutations est complétée de
chaque permutation PP. La liste finale des permutations (P) est
disponible pour le programme appelant la procédure (return). Exemple: appel de la
procédure avec le nombre 12345 et résultat de l'exécution en bleu. |
||
|
|
Sortie sous forme numérique Les chiffres de chaque permutation sont sommés (add) avec la pondération en puissance 10 qui correspond à la position du chiffre dans
le nombre. L'instruction op
permet de prendre les éléments dans une liste (en bref, d'éliminer les
crochets entourant la liste). |
||
Voir Programmation – Index
![]()
|
Index Permutation |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()