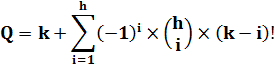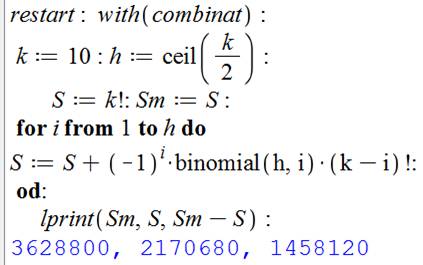NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/03/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	COMPTER – Combinatoire
Débutants COMPTER FAQ	NOMBRES & CHIFFRES			Glossaire COMPTER
INDEX Combinatoire	Nombres en général	Nombres en arrangements	Divisible par 2
	Pairs non placés	Nombre à k chiffres différents	Divisible par 5
	Terminale	Sommaire de cette page >>> Approche avec cas simples – 4 nombres >>> Consolidation avec cas à 6 nombres >>> Cas général >>> Programmation

Nombres pairs non bien placés

Compter de combien de façons on peut arranger la suite [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] de façon que les nombres pairs ne soient pas à leur place d'origine.

La réponse est 2 170 680. Mais comment s'y prendre?

Anglais: How many ways can the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 be arranged so that no even digit is in its original position?

There are 10! ways to arrange those digits. There are 9! arrangements in which 0 retains its position.

Voir Pannumérique

Approche avec cas simples – 4 nombres
Avec la suite [0, 1]	Une seule configuration convient: [1, 0].
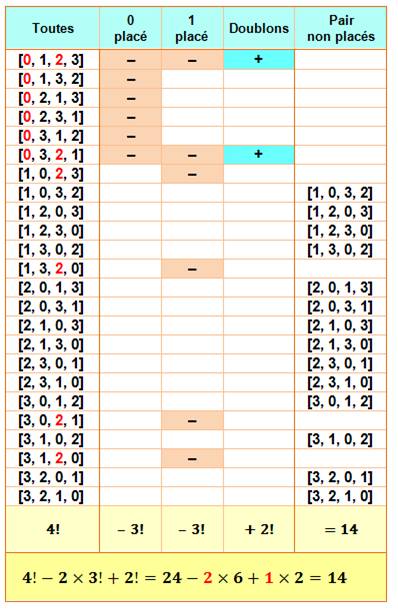
Avec la suite [0, 1, 2, 3]	On va montrer qu'il y a Q = 14 configurations valides et on va les dénombrer. Ex: [1, 0, 3, 2]
Ce tableau montre toutes les possibilités (colonne de gauche). Il y en a 4! = 24. On compte d'abord les cas où les nombres pairs sont bien placés: Le 0 est bien placé dans 3! = 6 cas (2^e colonne, en marron); Le 1 est bien placé dans 3! = 6 cas (3^e colonne, en marron); et nous devons compter les retraits en doublons (4^e colonne en bleu): 2 cas. Nous voyons s'amorcer une formule (ligne du bas) : 3! = 6 cas avec le 0 placé. En effet, il y a 3! possibilités pour arranger les trois autres nombres; 3! = 6 cas avec le 2 placé. => 2 x 3! pour bon placement de ces deux nombres; auxquels, il faut retirer les doublons. 2 cas avec le 0 et le 2 placés Parmi les 6 cas du 0 placé, il reste trois nombres (1, 2 et 3) à placer; Le 2 sera deux fois en tête, deux fois au milieu et 2 fois en queue. Soit deux cas avec le 2 bien placé.

Consolidation avec cas à 6 nombres
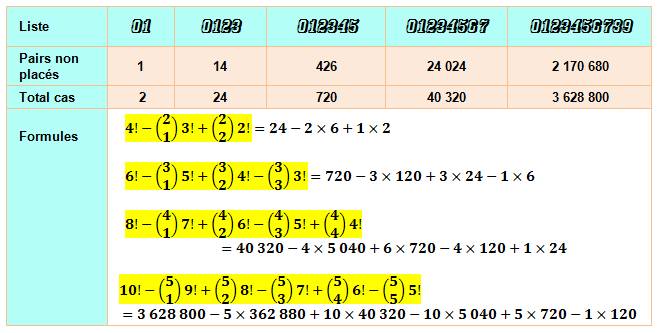
Pas question de lister tous les cas.	Liste [0, 1, 2, 3, 4, 5, 6] Il y a 6! = 720 (factorielle 6) permutations de ces six nombres. dont 426 cas sans nombres pairs bien placés.
Le principe est le même que ci-dessus avec une petite complication concernant les cas d'exclusion et inclusion.
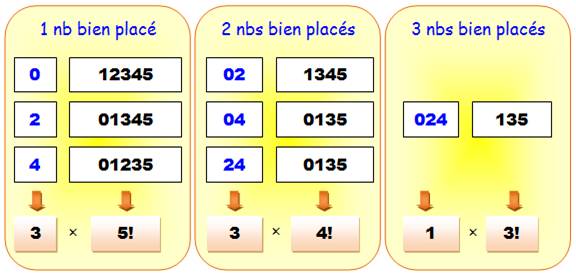
L'illustration permet de suivre le raisonnement. Bulle de gauche: pour un nombre bien placé (0, 2, 4), il y a trois fois 5! possibilités; Oui, mais, il y a des doublons (bulle du milieu). Ils sont présents trois fois en quantité égale à 4!; Et les "triplons"? (Bulle de droite): En éliminant les doublons, on élimine trop de monde; il faut restituer les triplons. Il y en a une fois 3!	Recensement des cas où les nombres pairs sont bien placés Exemple de lecture: à droite avec le 0, le 2 et le 4 bien placé: une seule possibilité de placement, mais, avec les trois nombres restants (1, 3 et 5), il y a factorielle 3 possibilités. Soit le produit: 1 x 3! Quantité de cas avec les nombres pairs non à leur place

Voir Factorielles – Arrangement, Permutations et Combinaisons

Cas général
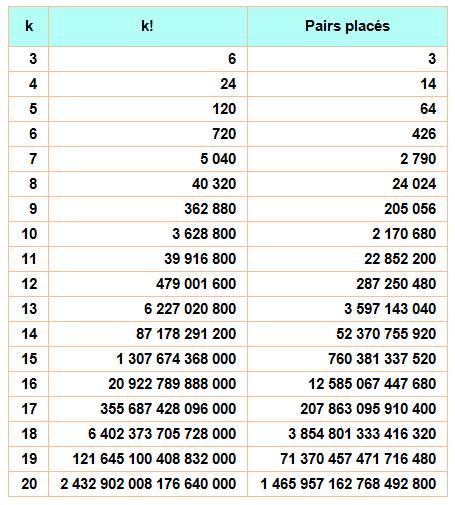
Tableau donnant la quantité de nombres pairs bien placés selon la quantité de nombres dans la liste Formule générale pout toute quantité de nombres dans la liste (paire ou impaire) Avec k la quantité de nombres et h = plafond (k/2) la quantité de nombre pairs Voir Coefficient du binôme

Programmation Maple
Programmation Maple pour une valeur de k donnée Programmation alternative: sans boucle; avec l'instruction somme cumulée (sum) Voir Programmation – Index Liste des valeurs pour k de 3 à 20 Voir Factorielle

Retour	Combinatoire – Rubriques D'un coup d'œil
Suite	Voir haut de page Jeux avec les chiffres – Index
Voir	Cartes Compter les nombres Dés Dominos Échecs Factorielle et ses cousines Grenouilles Jeux – Index Probabilités Somme de 4 carrés Triangle de Pascal
DicoNombre	Nombre 2 170 680
Cette page	http://villemin.gerard.free.fr/Denombre/aaaChiff/PairNP.htm