NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/04/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Fractions	NOMBRE PÉRIODIQUES				Glossaire Fractions
INDEX Fractions Représentation des nombres Types de nombres Nombres premiers	Débutants		Tour d'horizon
	Nombres décimaux		Nombres périodiques	Dichotomie de la période
	Premiers longs		Permutation circulaire	Extraction des décimales
	Fractions en 1/99…99		142 857	Égalité 0,999 = 1
		Sommaire de cette page >>> Exemple: nombre têtu142 857 >>> Nombres à permutations cycliques ou têtus >>> Propriétés >>> Densité des nombres premiers longs >>> Comment savoir si un premier est long? >>> Nombres têtus d'ordre 2 >>> Nombres têtus d'ordre n >>> Devinette avec 142 857

Nombres PREMIERS LONGS,

Nombres têtus,

Nombres phénix, ou

Nombres à permutation circulaire.

Nombres à développement décimal périodique dont la période est maximale. Alors, tous les multiples de ce nombre présentent une période faite des mêmes chiffres permutés en rond.

Comment les reconnaitre >>>

Liste: 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167 …

Table >>>

Anglais: long prime or full reptend prime

Also called long period primes or maximal period primes

Exemple du plus fameux

Nombre têtu 142 857

Nombre à développement décimal périodique 142 857 est la période de la fraction 1/7 1,7 = 0,142857 142857 … La longueur est égale à 6, soit 7 – 1, la valeur maximale possible. Multiples de ce nombre 142 857 x 1 = 142857 x 5 = 714285 x 4 = 571428 x 6 = 857142 x 2 = 285714 x 3 = 428571 Les produits se déduisent les uns des autres par permutation circulaire: décalage vers la gauche et le chiffre sortant à droite est réintroduit à gauche.

Voir la suite de toutes les propriétés "magiques" de ce nombre

Définition et propriétés

NOMBRES TÊTUS ou À PERMUTATIONS CIRCULAIRES ou PREMIERS LONGS

Définition Nombre premier dont l'inverse a un développement décimal périodique de période maximale. La longueur de la période est égale au nombre considéré moins 1. L = P – 1 Exemples: période pour quelques nombres premiers Quels sont ceux pour lesquels la période est maximale: 7, [1, 4, 2, 8, 5, 7] 11, [0, 9]) 13, [0, 7, 6, 9, 2, 3] 17, [0, 5, 8, 8, 2, 3, 5, 2, 9, 4, 1, 1, 7, 6, 4, 7] 19, [0, 5, 2, 6, 3, 1, 5, 7, 8, 9, 4, 7, 3, 6, 8, 4, 2, 1] 23, [0, 4, 3, 4, 7, 8, 2, 6, 0, 8, 6, 9, 5, 6, 5, 2, 1, 7, 3, 9, 1, 3] 29, [0, 3, 4, 4, 8, 2, 7, 5, 8, 6, 2, 0, 6, 8, 9, 6, 5, 5, 1, 7, 2, 4, 1, 3, 7, 9, 3, 1] Les nombres 7, 17, 19, 23 et 29 sont des nombres premiers longs. Le suivant est 109. Ils possèdent les mêmes propriétés que celles vues pour 1/7 = 0, 142857 … Liste des nombres premiers longs

Pour confirmer quelques exemples

52 631 578 947 368 421 x 19 = 999 999 999 999 999 999	Multiplié par un nombre quelconque de 1 à 18, il donne les mêmes chiffres, dans le même ordre, avec décalage Multiplié par 19, il donne un repdigit en 9.
344 827 586 206 896 551 724 137 931	Donne le même type de résultat jusqu'à 22 et pour 23 on ne trouve que des 9
0212 765 957 446 808 510 638 297 872 340 425 531 914 893 617	Va jusqu'à 47
Etc.	Ça continue!

Propriétés

Tous les nombres à permutations cycliques, inverses de nombres premiers, ont une période comprise entre (n – 1)/2 et n – 1. 1/13 = 0, 076 923 076 923 ... est cyclique de période 6, avec 6 = (13 – 1) / 2 Seuls ceux avec une période n – 1 sont têtus (premiers longs). Tous les nombres à permutations cycliques, inverses de nombres composés, ont une période qui est le PPCM des périodes des diviseurs premiers distincts. 1/21 = 0, 047 619 047 619... Or: 21 = 3 x 7 et 3 a une période de 1, alors que 7 à une période de 6 => 21 à une période de 6 x 1 = 6. Tous les nombres à permutations cycliques (ou têtus) ont les propriétés citées pour 142 857, avec les ajustements nécessaires. On ne sait pas s'il y en a une infinité.

Densité des nombres premiers longs
Propriété Conjecture d'Emil Artin (1927): La densité des nombres premiers longs, en nombre infini, tend vers: C = 0,373955... , la constante d'Artin. Cette conjecture n'est toujours pas démontrée (2016). Voir Racine primitive Formule = 0,373 955 813 619 202 288 05... >>> Le calcul de Shanks donnait 3/8 = 0,375

Voir Nombres premiers longs / Nombres têtus

Comment savoir si un premier est long?
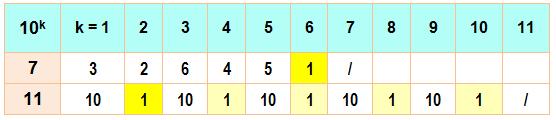
Prenons les premiers 7 et 11, et observons les restes des puissances de10 modulo 7 et 11: Le nombre 7 est un premier long; le résidu 1 n'arrive qu'en fin (10^6 = 142 857 x 7 + 1) Le nombre 11 ne l'est pas; le résidu 1 apparaît dès la puissance 2 (100 = 9 x11 + 1). Un nombre premier p est long si et seulement si le premier résidu modulo p est obtenu seulement pour 10^p – 1. La puissance de 10 qui conduit au premier résidu égal à 1 est appelé l'ordre du nombre (order of a number). Ordre de 7 = 6; ordre de 11 = 2; ordre de 13 = 6, etc. Plus généralement, la puissance de 10 peut être remplacée par la puissance d'un nombre k quelconque. L'ordre d'un nombre n en base b est le plus petit entier k tel que b^k 1 mod n Un nombre premier p est long si et seulement son ordre est p – 1. Bien sûr, il fait calculer les résidus des puissances de 10. Possible avec un moyen de calcul. Par exemple un logiciel de calcul comme Maple.^.
	Programme donnant l'ordre de chacun des nombres premiers Après réinitialisation, on lance une boucle d'exploration pour les nombres n de 5 à 50. On ne poursuit les calculs que si ce nombre est premier. Pour chacun, on explore les puissances de 10 jusqu'à 10^n – 1. La variable m mémorise la valeur du reste de la division de cette puissance par le premier n (modulo). Dès que cette valeur vaut 1, on imprime le nombre (n) et son ordre (i); puis on stoppe l'exploration (i := n – 1). L'impression montre les 12 nombres premiers entre 6 et 50. On y repère ceux qui sont longs: 7, 17, 19, 23, 29 et 47 Voir Autres programmations avec les périodiques
	Programme de recherche des seuls premiers longs. Même corps de programme. On ajoute une variable de test T qui vaut 1 si le nombre premier est long. On suppose qu'il est long a priori. Dès qu'un résidu vaut 1, cette hypothèse est annulée (T:= 0) et l'exploration est stoppée (i := n – 1). Si T résiste à un jusqu'à la fin, ou presque (n-2), alors on ajoute ce nombre à la liste L des premiers longs. Inutile de faire le calcul pour la puissance n – 1; le résidu est forcément égal à 1. Voir Table des premiers longs
	Programme avec instruction dédiée Un bon logiciel de calcul possède une instruction qui calcule directement l'ordre d'un nombre. Nous mettons en place une procédure (Plong). Pas obligatoire, mais intéressant pour constituer une bibliothèque de programmes utiles. L'instruction ithprime donne directement le nombre premier de rang n. On calcule son ordre avec l'instruction spéciale (order en base 10 pour p). On retourne p si l'ordre vaut p – 1. L'instruction séquence (seq) appelle la procédure pour n de 1 à 50.

Voir Programmation – Index

Têtus d'ordre 2:

Les multiples de P sont toujours obtenus par permutations circulaires de chiffres, mais à partir de deux périodes et non plus une seule.

Exemple (période 1 en vert et période 2 en bleu)

1/13	2/13	3/13	4/13	5/13	6/13	7/13	8/13	9/13	10/13	11/13	12/13
076 923		230 769	307 692					692 307	769 230		923 076
	153 846			384 615	461 538	538 461	615 384			846 153

Le résultat oscille entre les permutations des chiffres de 2 nombres.

Les autres têtus d'ordre 2: 13, 31, 43, 67, 71, 83, 89 …

Propriétés

Notez la relation entre les deux périodes: 153 846 = 2 x 76 923.

Configurations en 9:

076923 x 13 = 999999

076 + 923 = 999

07 + 69 + 23 = 99

153846 x 13 = 1999998 => 999999

153 + 846 = 999

15 + 38 + 46 = 99

Rappel: pour conserver la longueur de la période à 6, on ajoute ceux qui dépassent à gauche à ceux de droite.

Têtus d'ordre n

Nombre à permutations cycliques dont les chiffres sont la permutation des chiffres de n nombres.

Ordre n	1	2	3	4	5	6	7	8	9
Plus petit Têtu	7	13	103	53	11	79	211	41	73

Ordre n	10	11	12	13	14	15
Plus petit Têtu	281	353	37	2 393	449	3 061

Curiosité: carré magique têtu

1/19	= 0,	0	5	2	6	3	1	5	7	8	9	4	7	3	6	8	4	2	1
2/19	= 0,	1	0	5	2	6	3	1	5	7	8	9	4	7	3	6	8	4	2
3/19	= 0,	1	5	7	8	9	4	7	3	6	8	4	2	1	0	5	2	6	3
4/19	= 0,	2	1	0	5	2	6	3	1	5	7	8	9	4	7	3	6	8	4
5/19	= 0,	2	6	3	1	5	7	8	9	4	7	3	6	8	4	2	1	0	5
6/19	= 0,	3	1	5	7	8	9	4	7	3	6	8	4	2	1	0	5	2	6
7/19	= 0,	3	6	8	4	2	1	0	5	2	6	3	1	5	7	8	9	4	7
8/19	= 0,	4	2	1	0	5	2	6	3	1	5	7	8	9	4	7	3	6	8
9/19	= 0,	4	7	3	6	8	4	2	1	0	5	2	6	3	1	5	7	8	9
10/19	= 0,	5	2	6	3	1	5	7	8	9	4	7	3	6	8	4	2	1	0
11/19	= 0,	5	7	8	9	4	7	3	6	8	4	2	1	0	5	2	6	3	1
12/19	= 0,	6	3	1	5	7	8	9	4	7	3	6	8	4	2	1	0	5	2
13/19	= 0,	6	8	4	2	1	0	5	2	6	3	1	5	7	8	9	4	7	3
14/19	= 0,	7	3	6	8	4	2	1	0	5	2	6	3	1	5	7	8	9	4
15/19	= 0,	7	8	9	4	7	3	6	8	4	2	1	0	5	2	6	3	1	5
16/19	= 0,	8	4	2	1	0	5	2	6	3	1	5	7	8	9	4	7	3	6
17/19	= 0,	8	9	4	7	3	6	8	4	2	1	0	5	2	6	3	1	5	7
18/19	= 0,	9	4	7	3	6	8	4	2	1	0	5	2	6	3	1	5	7	8

Somme 81 sur les lignes et les colonnes, c'est normal; pour les diagonales c'est raté.

Retour	Dichotomie de la période des nombres périodiques Théorème de Midy ou de la demi-somme des périodes
Suite	Développement décimal des fractions Table des nombres premiers longs Permutations circulaires des nombres périodiques Nombres têtus – Parmi ses cousins Nombres premiers longs – Table
Voir	Calcul mental – Index Fractions continues Fractions de Farey Jeux – Index Nombres en N/999… Nombres rationnels Théorie des nombres – Index
DicoNombre	Nombre 109
Sites	OEIS A00193 - Full reptend primes: primes with primitive root 10. Full Reptend Prime – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Tetu.htm