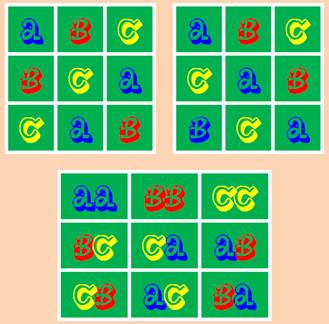
carrés latins et gréco-latins

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/11/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Bases et amusements				Glossaire Carrés magiques
INDEX Carrés magiques	Latin	Gréco-latin	Avec 0 à 9	Vers Magiques
	Cartes à jouer	Jeux (à trous)	Décimal	Sudoku
		Sommaire de cette page >>> Types de carrés mathématiques >>> Approche du carré latin >>> Définition >>> Propriétés et construction >>> Carré latin 1 à 5 >>> Construction – Exemples simples >>> Carré latin amusant >>> Application – Tournoi de tennis >>> Application – Tournoi d'échecs >>> Bilan

Carrés LATINS

Chaque ligne, comme chaque colonne, comporte des symboles (dessins, chiffres …) tous différents.

Un symbole pour les latins; deux pour les gréco-latins.

Ces carrés sont la base:

des carrés magiques et

des Sudoku.

Ils sont utilisés plus sérieusement pour organiser des tournois sportifs ou encore pour aider à la réalisation de choix: Plan d'expériences ou Design of Experiment (DOE).

Carrés latins d'ordre 1 à 4

Voir Types de carrés mathématiques

Étymologie

Vient de la tradition au XVIII^e siècle qui consistait à noter les lignes et les colonnes en lettres majuscules de l'alphabet latin et chiffres romains. La superposition de deux carrés latins nécessitait une seconde forme de lettres, les lettres grecques, d'où le nom de gréco-latin pour ces carrés formés de doublets.

Carrés latins – APPROCHE

Un tableau carré ce n cellules de côté.

Des symboles: dessins ou chiffres; il en faut n.

Placez ces symboles sur les lignes et les colonnes de sorte qu'il y ait un seul type de symbole par ligne et un seul par colonne.
(permutation figurée)

n = 2 – Nombres

1	2
2	1

n = 2 – Dessins

n = 3 – Nombres

1	2	3
2	3	1
3	1	2

n = 4 – Dessins

Amusement

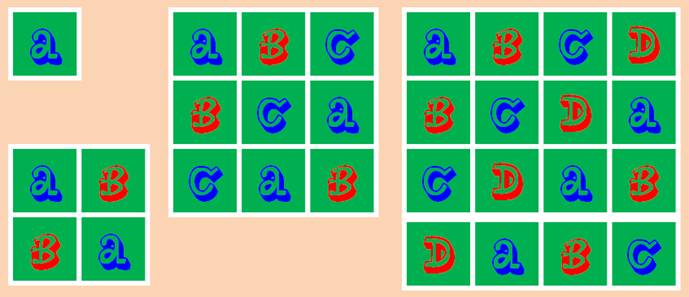
Ici, il faut placer deux fois le même symbole sur chaque ligne et sur chaque colonne.

Note: Il y a 1680 façons d'arranger les 3 symboles sur le damier 3 x 3.

Carrés latins – DÉFINITIONS

Classique (Euler 1782)

Tableau n par n

de n motifs (symboles, chiffres, dessins, couleurs …)

répartis de manière qu'ils ne se retrouvent qu'une seule fois dans chaque ligne et chaque colonne (permutations figurées).

Le carré est dit d'ordre n.

Carré Normalisé ou réduit ou standard

Constitué de nombres successifs.

Le carré est normalisé si les chiffres successifs apparaissent dans l'ordre en première ligne, et première colonne.

Notation

Une notation (dite orthogonale) consiste à donner les numéros de ligne et colonne d'une cellule, puis le symbole présent dans cette cellule.

Soit, ici:

(1,1,A), (1,2,B), (1,3,C), (2,1,B), (2,2,C), (2,3,A), (3,1,C), (3,2,A), (3,3,B).

Carrés orthogonaux

Deux carrés latins sont orthogonaux si les paires, formées à partir des cellules de même rang, n'apparaissaient qu'une seule fois.

Les deux carrés du haut sont orthogonaux, car les paires réunies dans le tableau du bas sont toutes différentes. D'ailleurs toutes les paires possibles sont présentes: aa, ab, ac, ba, bb, bc, ca, cb, cc.

Voir Carrés gréco-latins / Méthode d'Euler

Voir Dénombrer

PROPRIÉTÉS & CONSTRUCTION

Carré latin élémentaire avec des chiffres

On écrit la première ligne.

Les suivantes sont obtenues par permutation circulaire de cette première ligne. Dit autrement: on décale d'un cran à chaque ligne.

La somme sur les lignes et les colonnes est celle des chiffres utilisés:
8 + 6 + 4 + 2 = 20

8	6	4	2
4	2	8	6
2	4	6	8
6	8	2	4

Carré latin normalisé

Les chiffres sont dans l'ordre en première ligne et première colonne.

Le carré est réduit si, en plus, il utilise les nombres de 1 à n (comme ceux qui suivent).
La somme magique est alors: n(n+1)/ 2.
Soit: 10 pour le carré latin d'ordre 4.

2	4	6	8
4	6	8	2
6	8	2	4
8	2	4	6

Voir Propriétés – Suite

Merci à Gil M. pour sa lecture attentive

Carré latin avec nombres de 1 à 5

Carré latin 5 x 5.

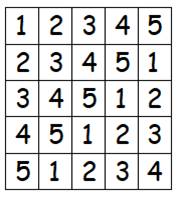
Chiffres de 1 à 5.

Une seule fois le même chiffre par ligne et par colonne.

Il existe, évidemment, de nombreuses combinaisons donnant la somme magique de 15.

On les obtient en inversant les lignes ou aussi les colonnes ou les deux à la fois.

Il y en a tellement, que l'on peut fixer d'autres contraintes.

1	2	3	4	5
4	5	1	2	3
2	3	4	5	1
5	1	2	3	4
3	4	5	1	2

Ce carré présente en effet d'autres figures comprenant les chiffres une seule fois:

La croix au centre.

Le centre et les quatre sommets.

Les pandiagonales (diagonales reconstituées, comme 2, 1, 5, 4 et de l'autre côté 3).

Et, beaucoup d'autres formes.

1	2	3	4	5
4	5	1	2	3
2	3	4	5	1
5	1	2	3	4
3	4	5	1	2

Construction – Exemples simples

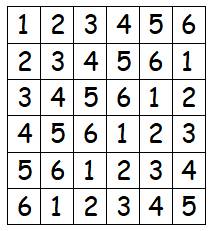
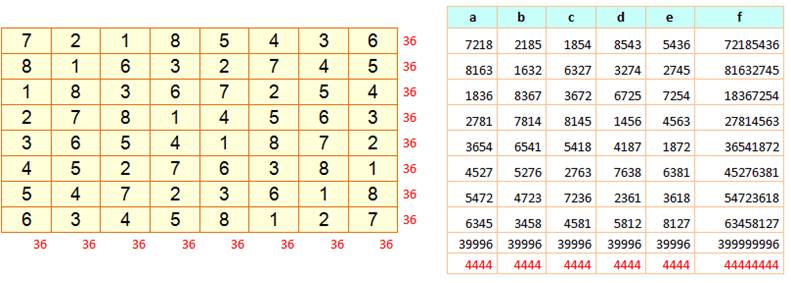
Un carré latin de 5 x 5 avec les nombres de 1 à 5:

Pour la première ligne écrivez la première ligne avec les nombres qui se suivent.

Pour la deuxième ligne, vous décalez la première ligne d'un cran et le premier nombre passe en queue dans la place vide.

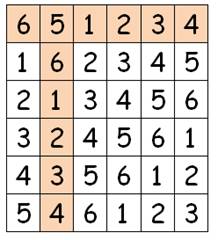
Pour la troisième ligne, vous décalez la deuxième ligne d'un cran et le premier nombre passe en queue dans la place vide.

Etc. jusqu'à la cinquième ligne.

Ce serait la même chose avec 6 ou n'importe quel autre nombre.

On obtient d'autres solutions en échangeant les lignes ou les colonnes.

Ici, la colonne 6 est passée en colonne 2 et la ligne 6 est passée en ligne 1.

Carré latin 5 x 5

Carré latin 6 x 6

Le même avec deux permutations

Carré latin amusant

Ce carré est bien latin: somme identique sur lignes et colonnes, et égale à 36, somme des nombres de 1 à 8 (1/2 x 8 x 9 = 36)

Pris par paires horizontales successives la somme est 9: 7+2 = 9, 1+8 = 9, 5+4 = 9, etc.

Pris par quatre, il forme des nombres dont la somme est 39 996 = 9 x 4444 (colonnes a à e).

Pris par huit, il forme des nombres dont la somme divisée par 9 est égale à: 44444444 (colonne f).

Source: Borders Chess

Une application des carrés latins – Tournoi de tennis
Organisation d'un tournoi de tennis Trois garçons Alain, Bruno et Cyril Trois filles Emma, Fany et Gladys. Un tournoi de tennis où chaque garçon doit jouer avec chaque fille. Faire le planning à raison de trois matches par jour. Vocabulaire Les deux équipes sont les contraintes (blocking factors) et les jours sont les faits d'expérience (experiment treatment). Le tableau des matches est un carré latin. Celui-ci est typique; il en existe d'autres.		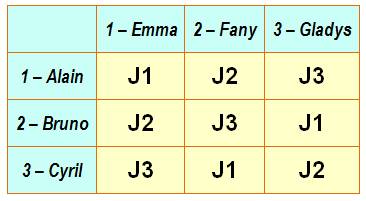Tableau des matches Le premier jour (J1), Alain joue contre Emma; Bruno contre Gladys et Cyril contre Fany. Avec ce plan, chaque jour, trois équipes différentes jouent et en fin de session, chaque garçon aura joué avec chaque fille.
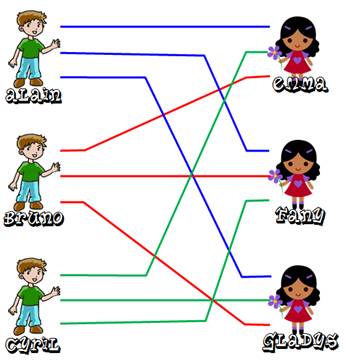
Construction – Première étape: interconnexions Relions par un trait chaque garçon à chaque fille. C'est classique.
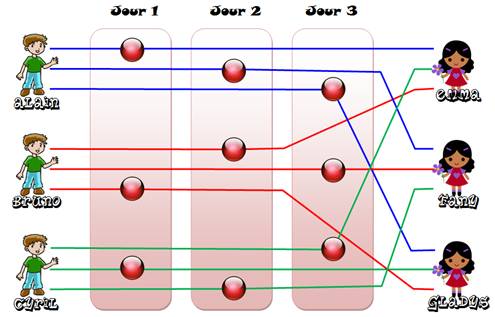
Construction – Deuxième étape: Allocation des jours Sur chaque trait, il s'agit de placer un seul point désignant un jour choisi pour le matche. La contrainte est que chaque jour doit comporter trois points dont le trait représente trois couples différents.
Remarques Notez que les garçons comme les filles n'ont pas joué entre eux. Ce qui reflète la situation de rencontres entre clubs ou entre nations. Pour un tournoi de tennis (deux joueurs) avec k équipes de chaque club (ou nation), il suffit e composer un carré latin d'ordre k.

Voir Organisation de tournois / Prénoms amusants

Tournoi d'échecs

Conditions initiales du tournoi

Deux équipes de quatre personnes: chaque jouer de l'une doit jouer contre chaque jouer de l'autre, soit seize parties.

Parties regroupée par quatre en quatre jours.

Chaque joueur ne joue qu'une fois par jour.

Résolution

Le carré latin en haut donne la solution: Le joueur A1 rencontre le joueur B1 le premier jour; il rencontre B2, le deuxième jour; etc.

Conditions supplémentaires

Chaque joueur aura joué autant de fois avec les blancs qu'avec les noirs

Chaque jour, chaque équipe jouera autant de fois avec les blancs et avec les noirs.

Résolution

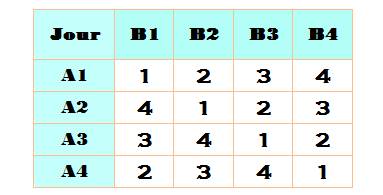
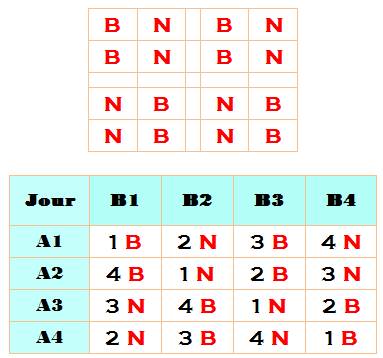
Nous avons besoin de l'aide d'un carré spécial: carré latin d'ordre 2, étendu par duplications à l'ordre 4.

En croisant avec le premier, nous obtenons le carré du bas.

Le joueur A1 joue deux fois avec les blancs et deux fois avec les noirs (ligne) …

Le joueur B1 aussi (colonne) …

Le jour 1, on joue aussi deux fois avec les blancs et deux fois avec les noirs (diagonale) …

Quatre joueurs contre quatre joueurs en quatre jours

Avec égalité entre parties avec les blancs et avec les noirs

La notation "blanc ou noir" en rouge s'applique aux joueurs de l'équipe A et l'inverse pour l'équipe B.

Voir Jeu d'échecs / Organisation de tournois

Bilan

On sait dire combien de carrés latins existent pour un ordre n donné. Par, contre les construire est plus problématique. Une méthode consiste à les construire ligne après ligne de sorte que les rectangles successifs soient latins.