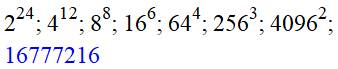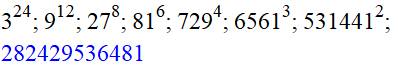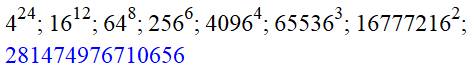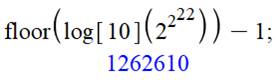|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PUISSANCE de 2 Table de valeurs |
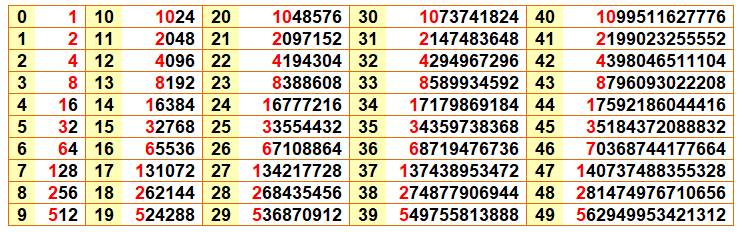
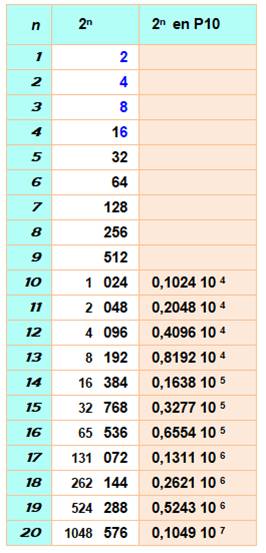
Table des puissances de 2 de 0 à 49
Remarquez
le même chiffre de tête (en rouge) pour les puissances avec écart de 10.
|
|
|
|
Le développement décimal de cette fraction débute par les
puissances de 2. Période du développement: 42. On note que 98 = 100 – 2; ce qui explique
cette propriété. Avec 1/999…98, on va encore plus loin avec les
puissances de 2.
Encore en puissances de deux; normal 98/2 =
49 |
|
Voir Fractions
engendrant des puissances
|
|
|
|
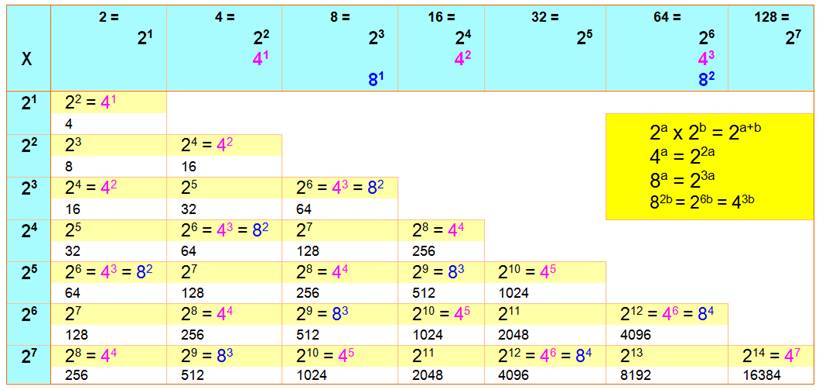
Comment passer d'une formule
à une autre ? 224 = 28 + 8 + 8 = 28
x 28 x 28 = 88 On a 24 = 3 x 8
=> pour l'exposant 8, le nombre est 23 = 8. Comment calculer la racine 8e de
ce nombre ? (224)1/8 = (88)1/8 = 8
|
|
Voir Nombre
158 et le jeu des quatre 4
|
|
||
|
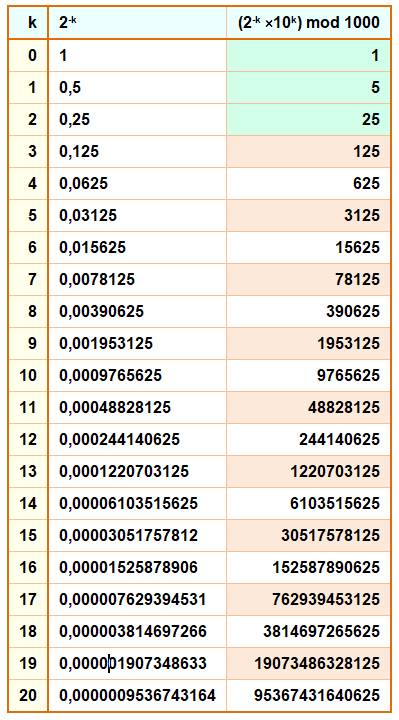
Propriétés Les puissances négatives de 2 se terminent
alternativement par 125 et 625, sauf les trois premières.
Devinette Quelles sont les
trois dernières décimales de 2-2020
? Le nombre 2020 est pair, les décimales sont donc:
625. |
|
|
|
Avec
explications |
|
||||
|
20 |
= |
1 |
|||
|
21 |
= |
2 |
|
||
|
2² |
= |
4 |
|
||
|
23 |
= |
8 |
|
||
|
24 |
= |
16 |
|
||
|
25 |
= |
32 |
|
||
|
26 |
= |
64 |
|
||
|
27 |
= |
128 |
|
||
|
28 |
= |
256 |
|
||
|
29 |
= |
512 |
|
||
|
210
|
= |
1 024 |
|
|
|
211 |
= |
2 048 |
Voir Jeu du
2048 |
|
|
212 |
= |
4 096 |
|
|
|
|
… |
|
|
|
|
216 |
= |
65 536 |
Sans
doute la seule puissance de 2 sans chiffre en puissance de 2: 1, 2, 4, 8. |
|
220
|
= |
1, 048 576 106 |
= 1 048 576 |
|
|
222 |
= |
4, 194 304 106 |
= 4 194 304 |
|
|
230
|
= |
1, 073 741
824 109 |
= 1 073 741 824 |
|
250 |
= |
1, 126... 1015 |
= 1 125 899
906 842 624 |
|
|
264 |
= |
1, 84... 1019 |
= 18 446 744
073 709 551 616 |
|
|
270 |
= |
1,18… 1021 |
= 1 180 591 620 717 411 303 424 Somme
des chiffres = 70 |
|
|
2100 |
= |
1, 26... 1030 |
=
1 267 650 600 228 229 401 496 703 205 376 |
|
|
2128 |
= |
3, 40... 1068 |
|
|
21000 |
= |
1, 07... 10301 |
=
10 7150860718 6267320948 4250490600 0181056140 4811705533 6074437503 8837035105
1124936122 4931983788 1569585812 7594672917 5531468251 8714528569 2314043598
4577574698 5748039345 6777482423 0985421074 6050623711 4187795418 2153046474
9835819412 6739876755 9165543946 0770629145 7119647768 6542167660 4298316526
2438683720 5668069376 |
|
|
22^22 |
= |
24 194 304 101 260 000 |
Voir ci-dessous |
Voir Limite de calcul à 228
= 268 435 456
Voir Table des
puissances de 2 – Mise en évidence des cycles sur les derniers chiffres
Voir Tables de
nombres de Mersenne 2k – 1
|
|
|
|
Cette valeur découle de la propriété
additive des exposants des puissances: 22 . 20 = 22 + 0 = 22 => 20 = 1 |
|
|
|
|||||
|
|
Toutes ces puissances de 2 se terminent de
plus en plus par les mêmes chiffres. Valeur
des derniers chiffres pour n successifs:
|
||||
|
= 2 ^ (2 ^22) = 2 ^ 2 ^ 22 = 2 4
194 304 Calcul de
la quantité de chiffres de ce
nombre:
|
Avec seulement quatre " 2 ", on
atteint cette valeur spectaculaire. Voir Puissances
à étages
La valeur
du nombre n'est pas atteignable avec un outil
de calcul classique. En revanche, la quantité de chiffres est représentée
par le plafond du logarithme en base 10 du nombre. Ici, un peu pus d'un
million de chiffres. |
||||
|
( ( ( ( 2² )² )² )²)² = 265
536 = 1019 729 |
Non Premier en
lui retirant 1. |
Somme des chiffres des puissances de 2
|
[1,
2], [2, 4], [3, 8], [4, 7], [5, 5], [6, 10],
[7, 11], [8, 13], [9, 8], [10, 7], [11, 14], [12, 19], [13, 20], [14, 22],
[15, 26], [16, 25], [17, 14], [18, 19], [19, 29], [20, 31], [21, 26], [22,
25], [23, 41], [24, 37], [25, 29], [26, 40], [27, 35], [28, 43], [29, 41],
[30, 37], [31, 47], [32, 58], [33, 62], [34, 61], [35, 59], [36, 64], [37,
56], [38, 67], [39, 71], [40, 61], [41, 50], [42, 46], [43, 56], [44, 58],
[45, 62], [46, 70], [47, 68], [48, 73], [49, 65], [50, 76], [51, 80], [52,
79], [53, 77], [54, 82], [55, 92], [56, 85], [57, 80], [58, 70], [59, 77],
[60, 82], [61, 74], [62, 85], [63, 89], [64, 88], [65, 86], [66, 109], [67,
110], [68, 103], [69, 89], [70, 70], [71, 86],
[72, 109], [73, 110], [74, 130], [75, 125], [76, 106], [77, 104], [78, 100],
[79, 110], [80, 112], [81, 107], [82, 124], [83, 122], [84, 118], [85, 128],
[86, 112], [87, 107], [88, 115], [89, 113], [90, 118], [91, 146], [92, 139],
[93, 125], [94, 151],
[95, 140], [96, 127], [97, 137], [98, 112], [99, 107], [100, 115] |
Voir Programme
de calcul de la somme des chiffres
Table de multiplication des puissances de 2
![]()
![]()
Table des puissances
de 2 de 1 à 120
|
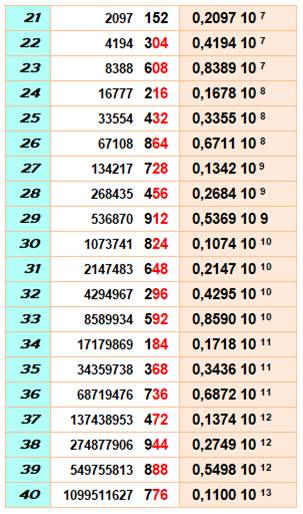
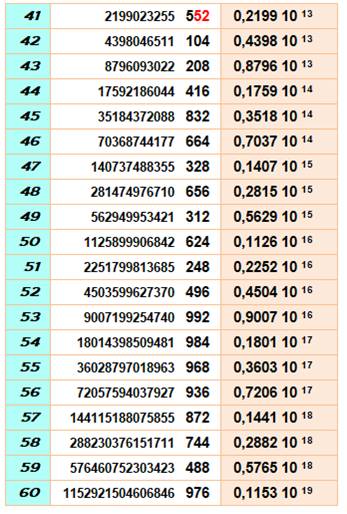
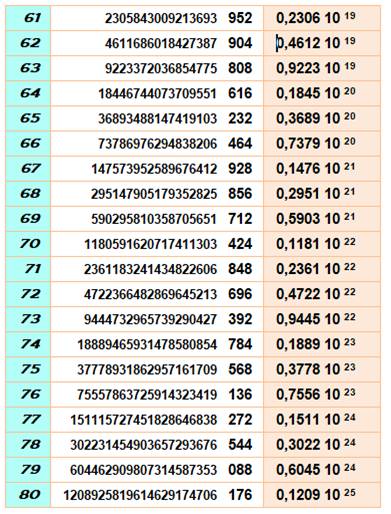
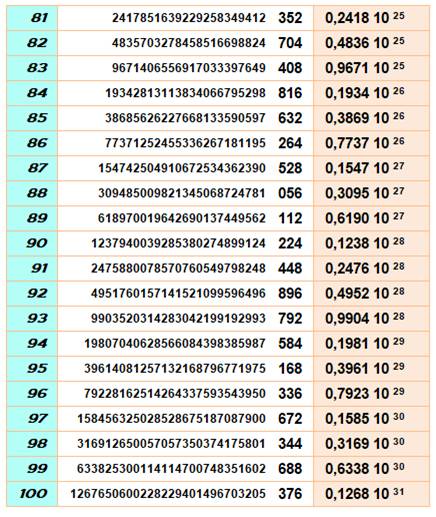
Mise en évidence des puissances avec leurs cycles de répétition des derniers chiffres
(couleurs pour les trois derniers chiffres). Les unités se répètent selon un cycle de longueur 4: 2, 4, 8, 6 Les deux
derniers chiffres se répètent selon un cycle de longueur 20: 4, 8, 16, 32, 64, 28, 56, 12, 24, 48, 96,
92, 84, 68, 36, 72, 44, 88, 76, 52 Les trois
derniers chiffres se répètent selon un cycle de longueur 100: 8, 16, 32, 64, 128, 256, 512, 24, 48, 96,
192, 384, 768, 536, 72, 144, 288, 576, 152, 304, 608, 216, 432, 864, 728,
456, 912, 824, 648, 296, 592, 184, 368, 736, 472, 944, 888, 776, 552, 104,
208, 416, 832, 664, 328, 656, 312, 624, 248, 496, 992, 984, 968, 936, 872,
744, 488, 976, 952, 904, 808, 616, 232, 464, 928, 856, 712, 424, 848, 696,
392, 784, 568, 136, 272, 544, 88, 176, 352, 704, 408, 816, 632, 264, 528, 56,
112, 224, 448, 896, 792, 584, 168, 336, 672, 344, 688, 376, 752, 504. La
période pour m derniers chiffres: Lp = 4 . 5m – 1, et la période
commence à partir de 2m Pour m =
3, on retrouve bien: 4 x 52 = 100 et elle commence pour n = 3 à 23
= 8; on la retrouve en n = 103. Bilan pour m successifs de 1 à 10: 4, 20, 100, 500, 2 500, 12 500, 62 500,
312 500, 1 562 500, 7 812 500 … |
Voir Propriétés des
puissances de 2
![]()

Voir Programmation
– Derniers chiffres des puissances
|
|
||
|
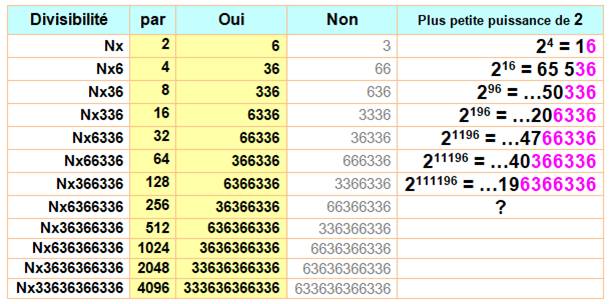
Recherche Recherche
des puissances de 2 dont les derniers chiffres sont 3 ou 6. On
utilise la propriété suivante: Alors, on teste la divisibilité des nombres en 3
et 6 de plus en plus grand, divisibles par les puissances de 2 successives. |
Résultat Nx6 désigne un nombre N suivi d'un chiffre
inconnu puis d'un 6. On teste l'ajout d'un 3 ou d'un 6 devant le
nombre précédent. Si ce nouveau nombre est divisible par la prochaine
puissance de 2, on le conserve (colonne "oui"). La colonne de droite montre les puissances de 2
qui satisfont le critère en 3 et 6. Il se trouve qu'un seul des deux cas
marche à chaque fois. La plus grande puissance de 2 trouvée est 1 111
196. La prochaine n'est pas 11 111 196. |
|
|
Table des premières occurrences
|
||
Voir Brève
715 / Nombre
6 366 336
![]()
|
Suite |
|
|
Autour des puissances de 2 |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()