|
Édition du: 19/11/2023 |
|
INDEX |
Types de Nombres – Motifs |
|||
![]()
|
NOMBRES SANDWICHES
Nombres dont les chiffres présentent une
répartition particulière:
Quelles sont toutes les possibilités ?
|
||
|
|
Sommaire de cette page >>> Le
plus petit: 312132 >>> Avec
les deux 4 >>> Avec
les deux 5 – Faisabilité ? >>>
Avec 7 et 8 >>> Double-sandwiches |
Débutants Glossaire |
|
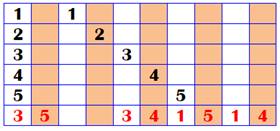
Avec deux 1 et deux 2 La grille montre
deux 1 avec la place entre les deux chiffres pour y loger un autre chiffre. La ligne
suivante montre les deux 2 avec deux places libres pour deux chiffres autres. La dernière ligne
montre à l'évidence qu'il est impossible de combiner les deux lignes du haut
pour en faire une telle que les 1 entourent un chiffre et les 2 entourent
deux chiffres. |
Les 1 occupent des cases
ocre. Les 2 occupent une ocre et
une blanche. D'où incompatibilité pour
les réunir en une seule ligne. |
|
|
Avec deux 1, deux 2 et deux 3 Même principe en
ajoutant les deux trois avec un espace permettant d'y loger trois chiffres. Bingo ! Les
trois lignes se rassemblent en une seule qui satisfait les règles. Le nombre retourné
est aussi un nombre sandwich. |
|
|
|
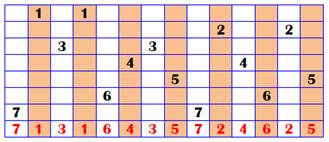
Analyse systématique On positionne le
nombre 3 qui présente le plus grand écart, lequel ne peut occuper que deux
positions:
Le couple de 2
prend place dans les cases vides. On élimine les cas où le 2 rencontre une
case déjà occupée par 3 (rouge). Est-ce que le
couple de 1 peut être logé ? Si oui, c'est
gagné. Ce cas gagnant
se présente deux fois et on retrouve bien un nombre 312 132 et son retourné
231 213. |
Toutes les possibilités => deux solutions
|
|
|
Avec deux 4 en plus Une solution se dégage en repoussant les deux vers la droite. |
|
||
|
Logique de remplissage Ces huit chiffres rouges couvrent autant de cases blanches que de
cases roses. Les quatre premières lignes offrent six blanches et deux roses qui permettent
cette alternance. Soit le nombre trouvé et son retourné. |
|
||
|
Avec deux 5 en plus Nous devons placer les chiffres 1, 1, 2, 2, …5, 5
en position 1, 2, 3, … 10. Un chiffre k est positionné k + 1 places plus
loin. Si k est pair, un des chiffres est position paire
(PP) et l'autre en position impaire (PI). Les chiffres 2 et 4 occupent 2 PP
et 2PI Il reste 3 PP et 3PI pour (1, 2, 3). Or, si k est impair, les deux chiffres sont en
position de même parité. Avec (1, 2 et 3), on aura, par exemple, 2PP et 2 PI ou encore 4PP et 2PI, mais
toujours des quantités paires incompatibles avec 3 PP et 3PI. Impossible avec ces paires de cinq chiffres. |
Configuration impossible Avec cinq paires de chiffres
La ligne rouge montre une possibilité, mais sans possibilité de loger les 2. |
||
|
Formulation Si n est la quantité de couples de chiffres et 2r est la quantité de chiffres
pairs, alors l'égalité suivante doit être vérifiée pour que la configuration
soit possible:
Conclusion: l'expression de droite doit être paire. Les crochets indiquent:
arrondi vers le bas (valeur plancher). |
Application de la formule
|
||
|
À
droite, une des solutions explicitées avec 7 : Les plus petits nombres avec 7 et
avec 8: Nombre 14 167 345 236 275 Nombre
1 318 637 245 268 475 |
|
||
|
Les 2 x 26 solutions avec 7
|
Les 43 solutions avec 8 débutant par un 1 Il y a 2 x
150 solutions
|
||
|
Le double-sandwich 123 est impossible. Il s'agit de positionner neuf chiffres dont trois 1, trois 2 et trois 3
avec la même règle d'espacement. La barre des 3 ne prend qu'une seule position La barre du 2 est impossible à placer. La technique de test consiste à faire glisser les barres
horizontalement de manière à obtenir un seul chiffre dans chaque colonne. |
|
||
|
Le double-sandwich 1234 est impossible. Après avoir positionné les barres du 4 et du 3, impossible de placer
la barre du 2. Sauf erreur, le plus petit cas possible se présente pour 123456789. |
|
||
|
Double-sandwiches pour 1 à 9 L'utilisation de tous les chiffres trois fois produit un triple nombre
pannumérique. Une solution explicitée
Les trois solutions, chacune avec son retourné (6
nombres de 27 chiffres) 181
915 267 285 296 475 384 639 743
/ 347 936 483 574 692 582 762
519 181 191 218
246 279 458 634 753 968 357 / 753 869 357 436 854 972 642 812 191 191 618
257269 258 476 354 938 743 / 347 839 453 674 852 962 752 816 191 |
|||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |