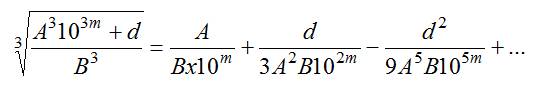type de nombres: nombres zébrés

Ce site est désormais accessible en

et pour cette page voir le lien en fin de page

For this page, refer to the link at the bottom.

22 Novembre 2025

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/03/2026 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Nombres	MOTIFS avec CHIFFRES			Glossaire Nombres
INDEX Motifs et chiffres	Ondulants	Zébrés	Croissants	Ascendants
INDEX Motifs et chiffres		Sommaire de cette page >>> Nombres zébrés >>> Une façon d'engendrer des nombres >>> Idem avec des décimales récurrentes >>> Les zébrés en formule

NOMBRES TRIANGLES

Une race de nombres, plutôt ludique, qui se situe à mi-chemin entre

les nombres rationnels, dont les décimales sont périodiques, et

les nombres irrationnels (comme racine de 2), dont les décimales sont aléatoires.

Les décimales de ces nombres présentent des suites de décimales similaires, semblables aux zébrures du fameux animal.

0, 111 2222 33333 44444 …

0, 852 852 852 963 963 741 741 111111111111 …

Anglais: Zebra number

Famille	Nombre / Forme
Définition	NOMBRE ZÉBRÉ Nombres dont les décimales sont des motifs successifs de chiffres. Exemples: 0, 001 002 003 004 … 0, 222 333333 555555 … 2323, 96969696 65436543 …
Rappel	NOMBRE RATIONNELS (ou PÉRIODIQUES) Nombres dont les décimales se répètent individuellement ou par groupe 0, 50000… = 1/2 0, 33333 … = 1/3 0, 142857 142857 … = 1/7 Voir Nombres périodiques
Multiplication par 100..01	À titre de mise en bouche … 124557 x 100001 = 123457123457 123457 x 1000001000001 = 123457123457123457 123457 x 1000000010000000100000001 = 123457001234570012345700123457 1001³ = 1003003001 1001⁴ = 1004006004001 Voir Curiosité avec le triangle de Pascal

Une façon d'engendrer ces nombres

Soit c un chiffre de 0 à 9. Comment, avec une formule, placer des chiffres différents l'un après l'autre? Avec une formule récurrente impliquant une puissance de 10:

(c) = 10 f(c – 1) + c

Voir Nombres Pannumériques

Idem avec deux chiffres: f(c) = 100 f(c – 1) + c

Avec deux chiffres et génération aléatoire de c

Une façon d'engendrer ces nombres

avec des décimales récurrentes

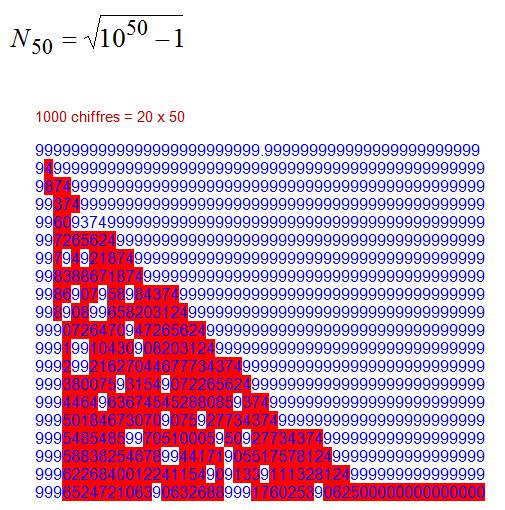
Kevin Brown Il a eu l'idée de prendre la racine carrée des nombres engendrés ci-dessus (f(0) avec nombres).
Surprise! Les rangs impairs produisent des nombres irrationnels avec séquence de décimales répétitives. Ce sont des nombres zébrés.

La racine carrée de nombres pannumériques étendus d'ordre impair

donne une sorte de repunit.

Pour f(101), on obtient un nombre de 100 chiffres composé exclusivement de 1 (repunit)

101, 12345679012345679012345679012345679012345679012345679012345679012345679012345679012345679012345679001,

1 1111111111 1111111111 1111111111 1111111111 1111111111

.111111111 1111111111 1111111111 1111111111 1111111111

Note: avec f(0) sur chiffres (et non nombres), la racine carrée donne une suite de 1 beaucoup plus modeste.

Les ZÉBRÉS en formule

Paradoxal ou magique, il existe des formules, complexes certes, qui produisent des nombres zèbrés irrationnels

Racine curieuse (R. Yéléhada)

Le motif se dessine de mieux en mieux avec de grandes puissances.

Forme générique: N = (10ⁿ – 1) ^1/k

Robert Israel

Jason Earl

Chasseur de zèbres; Il en a calculé d'autres, dont les suivants avec la même formule générique.

Darrell Plank

Avec une racine cubique.

Explication: série de Taylor

En bref, la formule de la racine cubique peut s'exprimer d'une façon approximative par une somme de termes dont la quantité permettra de d'améliorer l'approche de la valeur exacte

Si les premiers termes sont des inverses de puissances de dix, les valeurs absolues qui vont apparaître dans la division seront isolées par ces puissances de dix

Les zébrures se forment du fait de la présence de fraction qui produisent des nombres périodiques et du décalage des décimales provoqué par les puissances de dix au dénominateur.

Autre exemple baptisé "1481" Par Pickover

D'après Clifford Pickover (Magiques mathématiques)

Voir	Nom des nombres Nombres à motifs Nombre Repunit Nombre Pannumérique Nombre Périodiques Nombre permutation
Sites	Les nombres zébrés par Jean-Paul Delahaye Les nombres zébrés par Éric Buchlin (avec programme) The Mathematics of Oz - Mental Gymnastics from Beyond the Edge – Clifford Pickover - Cambridge University Press – 2002 – Avec de larges extraits du livre, dont le chapitre sur les nombres zébrés
Livre	Magiques mathématiques – 108 énigmes et autres curiosités - Clifford Pickover – Dunod - 2003
Cette page	http://diconombre.fr/aNombre/TYPFORM/Zebre.htm