|
|||||||||||||||||||||||||||||||||
PN:
Pannumériques
![]()
|
NOMBRES PANNUMÉRIQUES & REPDIGITS 111 111 111
x 111 111 111 = 12 345 678 9 876 543 21 Ce repdigit au carré
donne un pannumérique double palindromique |
|
|
||||||
|
||||||
|
PYRAMIDES - Curiosités |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
obtenez une somme égale à un repdigit: 11 111 ou 22 222 ou …
|
||||||||||||||||||||||||||||||||||||||
|
Avec 99 999
pour somme
Exemples 1234 = 98765 = 99999 1235 = 98764 = 99999 1243 = 98756 = 99999 1246 = 98753 = 99999 1253 = 98746 = 99999 … 2134 = 97865 = 99999 3124 = 96875 = 99999 8576 = 91423 = 99999 … |
Avec xx xxx
pour somme (x Exemple avec 8
Quelles sont les sommes qui donnent 8 ou 18 (avec
retenue). 8 = 0 + 8 = 1+ 7 = 2 + 6 = 3 + 5 18 = aucune (9 + 9 ne convient pas car le 9 est
répété). soit quatre sommes qui conviennent. Or il en faut 5. donc impossible. Raisonnement semblable pour les autres repdigits. Avec le 1, par exemple: seule opération sans retenue 1 = 0 + 1, toutes les
autres ont avec retenues: 2+9 = 3+8 = 4+7 = 5 + 6 1,0 à gauche est impossible car arriverait forcément une
retenue qui donnera une somme égale à 2; 1, 0 à droite nécessite une somme
comme 9+2 = 11 puis des sommes tenant compte de la retenue propagée soit:
7+3, 6+4, et il en manque une pour arriver au bout. |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
obtenez une différence égale à un repdigit: 11 111 ou 22 222 ou … |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Avec 1
Toutes (24) 13579 - 2468 = 11 111 13597 - 2486 = 11 111 13759 - 2648 = 11 111 13795 - 2684 = 11 111 13957 - 2846 = 11 111 13975 - 2864 = 11 111 15379 - 4268 = 11 111 15397 - 4286 = 11 111 15739 - 4628 = 11 111 15793 - 4682 = 11 111 15937 - 4826 = 11 111 15973 - 4862 = 11 111 17359 - 6248 = 11 111 17395 - 6284 = 11 111 17539 - 6428 = 11 111 17593 - 6482 = 11 111 17935 - 6824 = 11 111 17953 - 6842 = 11 111 19357 - 8246 = 11 111 19375 - 8264 = 11 111 19537 - 8426 = 11 111 19573 - 8462 = 11 111 19735 - 8624 = 11 111 19753 - 8642 = 11 111 |
Avec 2
Toutes (12) 25718 – 3496 = 22 222 25871 - 3649 = 22 222 27158 - 4936 = 22 222 27185 - 4963 = 22 222 28571 - 6349 = 22 222 28715 - 6493 = 22 222 31478 - 9256 = 22 222 31487 - 9265 = 22 222 31748 - 9526 = 22 222 31784 - 9562 = 22 222 31847 - 9625 = 22 222 31874 - 9652 = 22 222 |
Avec 3 Deux seules
possibilités
Objet
d'un casse-tête classique dit Cryptarithme Voir Résolution |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Avec 4 Toutes (18) 46279 – 1835 = 44 444 46297 - 1853 = 44 444 46819 - 2375 = 44 444 46981 - 2537 = 44 444 47629 - 3185 = 44 444 47962 - 3518 = 44 444 48169 - 3725 = 44 444 48196 - 3752 = 44 444 49627 - 5183 = 44 444 49681 - 5237 = 44 444 49762 - 5318 = 44 444 49816 - 5372 = 44 444 51238 - 6794 = 44 444 51427 - 6983 = 44 444 52138 - 7694 = 44 444 53416 - 8972 = 44 444 54127 - 9683 = 44 444 54316 - 9872 = 44 444 |
Avec 5 Toutes (42) 56789 – 1234 = 55 555 56798 - 1243 = 55 555 56834 - 1279 = 55 555 56879 - 1324 = 55 555 56897 - 1342 = 55 555 56942 - 1387 = 55 555 56978 - 1423 = 55 555 56987 - 1432 = 55 555 57239 - 1684 = 55 555 57248 - 1693 = 55 555 57689 - 2134 = 55 555 57698 - 2143 = 55 555 57869 - 2314 = 55 555 57896 - 2341 = 55 555 57941 - 2386 = 55 555 57968 - 2413 = 55 555 57986 - 2431 = 55 555 58319 - 2764 = 55 555 58346 - 2791 = 55 555 58679 - 3124 = 55 555 58697 - 3142 = 55 555 58724 - 3169 = 55 555 58769 - 3214 = 55 555 58796 - 3241 = 55 555 58967 - 3412 = 55 555 58976 - 3421 = 55 555 59417 - 3862 = 55 555 59426 - 3871 = 55 555 59678 - 4123 = 55 555 59687 - 4132 = 55 555 59723 - 4168 = 55 555 59768 - 4213 = 55 555 59786 - 4231 = 55 555 59831 - 4276 = 55 555 59867 - 4312 = 55 555 59876 - 4321 = 55 555 61289 - 5734 = 55 555 61298 - 5743 = 55 555 61379 - 5824 = 55 555 61397 - 5842 = 55 555 61478 - 5923 = 55 555 61487 - 5932 = 55 555 |
Avec 6 Toutes (10) 69153 – 2487 = 66 666 69513 - 2847 = 66 666 71358 - 4692 = 66 666 71529 - 4863 = 66 666 71934 - 5268 = 66 666 73158 - 6492 = 66 666 73194 - 6528 = 66 666 73491 - 6825 = 66 666 74931 - 8265 = 66 666 75129 - 8463 = 66 666 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Avec 7 Toutes (12) 81256 – 3479 = 77 777 81472 - 3695 = 77 777 81526 - 3749 = 77 777 81742 - 3965 = 77 777 82156 - 4379 = 77 777 82516 - 4739 = 77 777 84172 - 6395 = 77 777 84712 - 6935 = 77 777 85126 - 7349 = 77 777 85216 - 7439 = 77 777 87142 - 9365 = 77 777 87412 - 9635 = 77 777 |
Avec 8 Toutes (0) |
Avec 9 Toutes (0) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
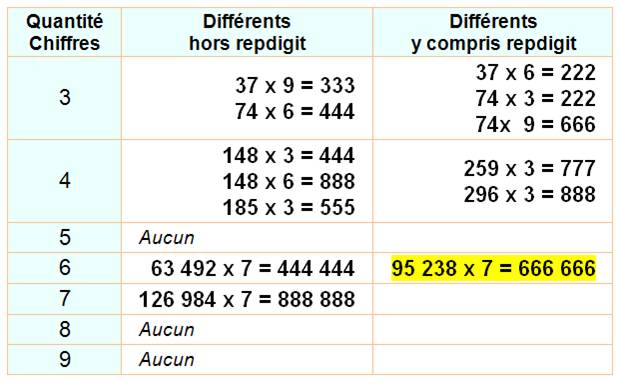
Énigme Trouver la valeur des lettres, toutes avec des
chiffres différents, telle que:
Un nombre comme GGG GGG formé avec un seul même chiffre est un nombre
uniforme ou repdigit. Solution La solution apparaît en jaune dans ce tableau. Le tableau donne toutes les solutions possibles
selon la quantité de chiffres et en distinguant si les chiffres du produit et
celui du repdit sont différents ou non.
|
|
Voir Cryptarithme
![]()
|
Suite |
|
|
Aussi |
|
|
DicoNombre |
|
|
Cette page |
![]()