|
||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ p Formes polynomiales
divisibles par 9. |
Amusement
|
Un
nombre retranché à son retourné
est toujours divisible par 9. Ex:
321 – 123 = 198 = 9 x 22 |
|
|
||
|
Critère |
Un nombre est divisible par 9 si la somme de ses chiffres l'est. Un nombre est divisible par 3 si la somme de ses chiffres l'est. Voir Divisibilité
par 3 |
|
|
En
pratique |
Faire la somme en retirant 9 ou ses multiples dès
qu'on le peut pour alléger le calcul. Le nombre est divisible par 9 si cette
somme est nulle ou multiple de 9. Voir Racine
numérique |
|
|
Exemple |
123 456 789 1 + 5 + 6 = 12 et 12
– 9 = 3 3 + 7 = 1 + 0 = 1 1 + 8 = 9 et 9 – 9 = 0 0 + 9 = 9 et 9 – 9 =
0 Plus astucieusement, on aurait pu arranger les
chiffres de manière à faire le plus possible des sommes égale à 9: 123 456 789 |
|
|
La démonstration repose sur la propriété suivante |
100000 … = 99999… + 1 = 9 x11111… + 1 et aussi, par exemple 7 000 = 7 x 9 x 111 +
7 Ce qui veut dire que 7000 divisé par 9 donne un
reste de 7. |
|
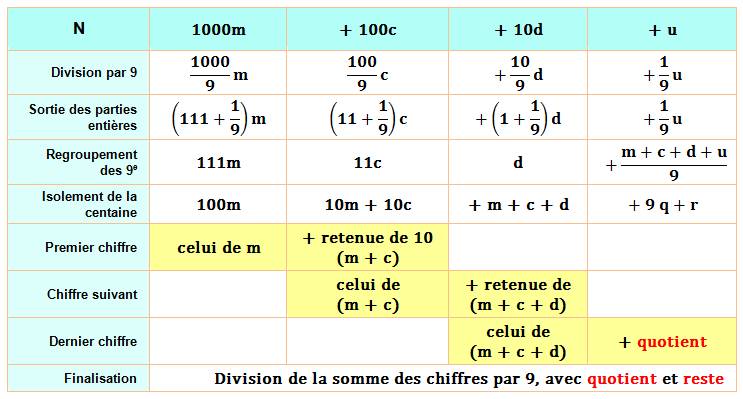
Soit un nombre et son développement décimal. |
N = … 103
m + 102 c + 10 d + u m = milliers; c
= centaines; d =dizaines et u = unités |
|
Sous cette forme en |
N = … (999+1)m + (99+1)c + (9+1)d + u |
|
En développant |
N = …999m + 99c + 9d + m + c + d + u |
|
En facteur pour le début |
N = … 9(111m + 11c + d) + m + c + d + u |
|
Si est un multiple de 9 |
N = 9k = … 9(111m + 11c + d) + m + c + d + u |
|
La partie droite de l'égalité doit être divisible
par 9; le terme en facteur par 9 l'est; le reste doit l'être. |
… m + c + d + u = 9h |
|
La propriété vaut pour 3 un facteur premier de 9. |
… m + c + d + u = 3h |
Voir Divisibilité
par 3 et sa preuve
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Méthode rapide valable pour tout nombre Ajouter le prochain chiffre à la somme (y compris
retenues) que vous venez de trouver. Le reste et égal à la somme dizaine et unité de
la dernière somme. |
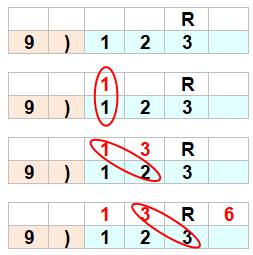
123 / 9 = 13 reste 6 45678 / 9 = 5075 R3 98765 / 9 = 10973 R8 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
À la façon américaine La disposition n'est pas très pratique en cas de retenues. |
La disposition est pratique.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Méthode rapide, identique pour
99 / Brève
893
|
|
|||
|
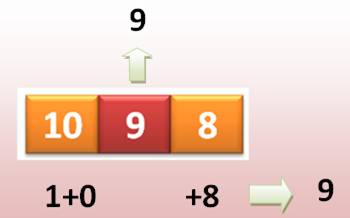
Deux chiffres |
Dizaine + 1 ou 10 – Unité. |
72 / 9 = 7 + 1 = 8 72 / 9 = 10 – 2 = 8 |
|
|
Trois chiffres |
1) Preuve par 9 pour retirez le reste. |
344 / 9 => 3 + 4 + 4 = 11
reste 2 344 – 2 = 342 divisible par
9 |
|
|
2) Si unité = 0, faites comme avec deux chiffres. |
720 / 9 = 80 |
|
Méthode amusante, mais il est parfois plus simple de faire la division
classique de tête. |
En bref: Dizaine = centaine Unité = 10
– unités Avec cas particuliers |
|
|
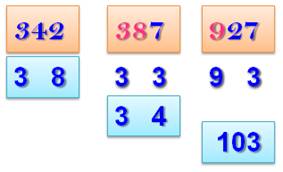
En détails 3) Prenez les centaines et le complément à 10 des
unités. |
342 => 3 et 10 – 2 = 8 342 / 9 = 38 |
|
|
|
4) Si le résultat est inférieur ou égal à la quantité
de dizaines, ajoutez 10. |
387 / 9 => 33 < 38
=> 33 + 10 = 43 387 / 9 = 43 |
|
|
5) Si le nombre est supérieur à 900, ajoutez
encore 10. (Notez
que dans ce cas la division est évidente: 9 suivi d'un multiple de 9). |
927 / 9 => 93 => 103 963 / 9 => 97 => 107 Merci à Jean-Baptiste T.
pour avoir remarqué ce cas |
|
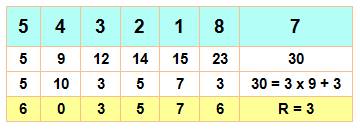
n chiffres |
En bref: Chaque chiffre est ajouté à la somme précédente. Le quotient par 9 du bout est ajouté à cette
somme. Dans le cas général, tenir compte des retenues. |
|
|
|
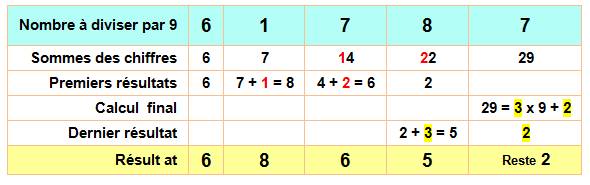
En détails (autre exemple) 1) Conservez le premier chiffre. |
61 787 / 9 61 |
|
|
2) Ajoutez le premier et le deuxième. |
6 + 1 = 72 |
|
|
3) Ajoutez le troisième à ce résultat. |
7 + 7 = 14 => 43 72 + 1 = 82 |
|
|
4) Répétez l'étape 3, autant de fois que
nécessaire. |
14 + 8 = 22 = 24 43 + 2 = 63 |
|
|
5) Pour le dernier, calculez la somme des chiffres. |
22 + 7 = 29 29 / 9 = 3 x 9 + 2 |
|
|
Résultat |
61 787 / 9 = 61826354
reste 2 |
|
En pratique |
Méthode pratique sur un exemple Sous le nombre écrire, les sommes cumulées. Ajoutez à chaque chiffre des unités, la retenue
de la somme suivante. Pour le dernier effectuer la division avec son
reste.
Autre exemple (avec propagation des
retenues)
|
|
Voir Propriété de la division par 9
/ Calcul mental – Index / Division
par 59
|
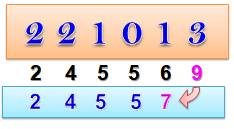
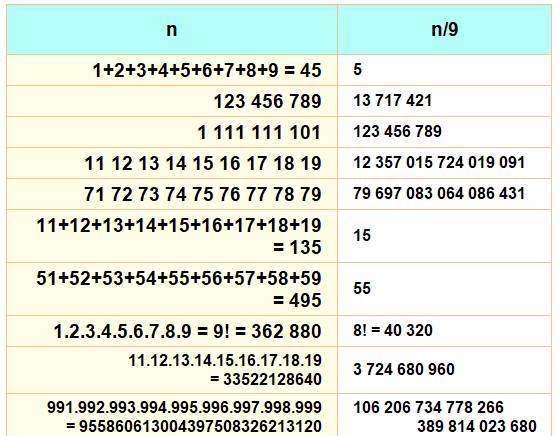
Quantité
de compositions à partir de ces neuf nombres sont divisibles par 9:
|
Voir Nombres
pannumériques / Pannumériques
partiels
|
|
||
|
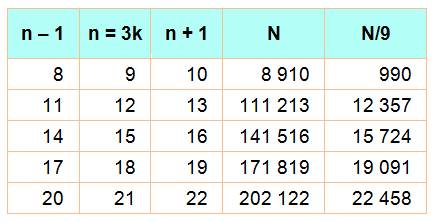
Affirmation |
Soit un nombre formé par la concaténation
de trois nombres consécutifs; si le nombre central est divisible par 3, le nombre
formé est également divisible par 9, ainsi que toute permutation de ce
nombre. |
|
|
Pourquoi? |
Soit n central divisible par 9. En termes de preuve par neuf, ses deux voisins
s'annihilent dans la division par 9.
|
|
|
Exemples |
|
|
|
|
||
|
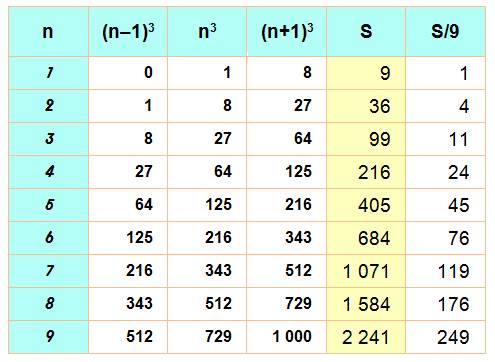
Affirmation |
9 | (n
– 1)3 + n3 + (n + 1)3 Rappel: la barre
verticale se lit "divise". |
|
|
Exemples |
|
|
|
Démonstration
par induction >>> |
|
|
Développons le polynôme: |
(n – 1)3 + n3 + (n + 1)3 = n3 – 3n2 + 3n – 1 + n3 + n3 + 3n2 + 3n + 1 = 3n3 + 6n |
|
Pour n = 1, c'est vrai. |
3 x 13 + 6 x 1 = 3 + 6 = 9 |
|
Supposons la formule vraie pour k. L'est-elle pour n + 1? |
3(n + 1)3 + 6(n + 1) = 3 (n3 + 3n2 +3n +1) + 6n + 6 = 3n3 + 9n2 + 15n + 9 |
|
Le premier terme est divisible par 9 selon
notre hypothèse. Le second l'est. La somme est donc divisible par 9 CQFD. |
= ( 3n3 + 6n ) + 9 (n² + n + 1) |
|
|
|||
|
Approche Prenons
l'exemple de deux nombres ayant la même somme de chiffres et calculons leur
différence:
Chacun
des nombres a le même reste lorsque divisé par 9, c'est d'ailleurs la somme
des chiffres (preuve par
neuf). |
231 – 141
= 90 (3x7x11)
– (3x47) = 2x3²x5 Division
par 9 de chacun: 231 = 25
x 9 + 6 141 = 15
x 9 + 6 231 – 140
= (25 – 15) x 9 = 90 |
||
|
Théorème La différence de deux nombres ayant la même somme
de chiffres est divisible par 9. Exemples 40 – 31 = 9 75 – 48 = 27 = 9 x 3 222 – 51 = 171 = 9 x 19 987 654 – 456 789 = 530 865 = 9 x 58 985 |
Démonstration Deux nombres avec la même somme de chiffres: - N1 et sa somme de chiffres k - N2 et sa somme de chiffres k Division par 9 (congruences): N1 mod 9 = k (ou sous-multiple de k) N2 mod 9 = k (ou sous-multiple de k) La différence est divisible par 9 et aussi par 3. |
||
Voir Application
aux nombres premiers
|
Énigme Combien
de nombres divisibles à la fois par 9 et par 5 peut-on former en ajoutant
trois chiffres après 666 ? Réponse Divisible
par 5 => unité 0 ou 5 Divisible
par 9 => somme des chiffres = 9k; or; 6 + 6 + 6 = 18; les trois autres
doivent faire une somme de 9k. Les 23 solutions 666000, 666900,
666810, 666720, 666630, 666540, 666450, 666360, 666270, 666180, 666090,
666990, 666405, 666315,
666225, 666135, 666045, 666945, 666855, 666765, 666675, 666585, 666495 Commentaires On
aurait le même jeu de trois chiffres avec 333 ou 666 ou tout nombre dont la
somme des chiffres est en 9k (118,126 …). Avec
tous les autre nombres, non-divisible par 9, on aurait 22 solutions: Exemple 123300, 123210,
123120, 123030, 123930, 123840, 123750, 123660, 123570, 123480, 123390, 123705, 123615,
123525, 123435, 123345, 123255, 123165, 123075, 123975, 123885, 123795
|
Voir Nombre 666
English corner
|
Numerals whose sum of digits is
divisible by 9 represent
numbers divisible by 9. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()