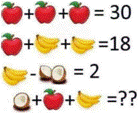Puzzle pannumérique

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/03/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puzzles arithmétiques
Débutants Cryptogramme	Formes		Glossaire Général
INDEX Pannumériques Puzzles	Pannumérique	Puzzles arithmétiques – Cryptarithmes
		Sommaire de cette page >>> Opération pannumérique >>> Formulation >>> Recherche d'une solution avec logique >>> Recherche par test et erreurs >>> Quantité de solutions >>> Tableau des solutions >>> La presse

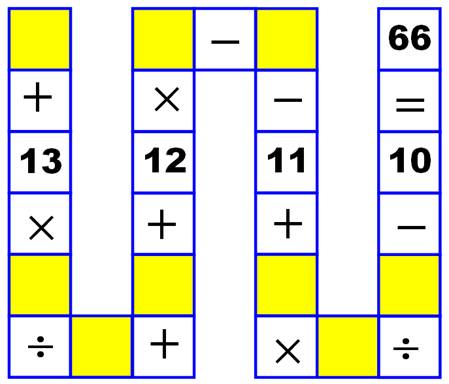
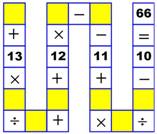
Opération pannumérique sur rail

Puzzle serpent

Puzzle vietnamien

La presse de mai 2015 se fait l'écho d'un problème d'arithmétique qui aurait été donné à résoudre à de jeunes enfants vietnamiens (8 ans!) de niveau CE2. Même si ce problème ne requiert que la maitrise des quatre opérations, il s'avère très complexe. Du moins, sans possibilité de résolution par raisonnement. Une tentative par essais–erreurs et ajustements va s'imposer. À moins d'avoir recourt à l'informatique.

Anglais: Viral problem from Vietnam

Opération pannumérique

Ce rail représente une opération utilisant tous les nombres de 1 à 13 dont le résultat est 66.

Les nombres de 10 à 13 sont positionnés sur un alignement sympathique.

Les signes des opérations sont indiqués

Problèmes

Retrouvez la position des nombres de 1 à 9 pour que l'opération soit juste.

Combien de possibilités?

Formulation

La première démarche va consister à remettre cette opération sous la forme conventionnelle et en respectant la priorité des opérations.

Nommons par des lettres les neuf nombres à retrouver.

La simplification consiste à regrouper à droite les valeurs numériques isolées

Évidemment les nombres a et d comme g et h sont permutables.

La quantité de solutions est donc un multiple de 4.

Forme linéaire

a +13b : c + d + 12e – f – 11 + g h : i – 10 = 66

Forme développée

Simplification et réarrangement

Recherche de solution logique
Somme algébrique des quatre termes simples	Min: 8 + 7 + 12 x 1 – 9 = 18 Max: 8 + 7 + 12 x 9 – 1 = 122
Terme en b et c	c divise b => c = {1, 2, 3, 4} pour avoir un entier Rien n'interdit d'avoir une fraction qui, ajoutée à la suivante, donnera un entier.
Terme en g, h et i	i divise g ou h ou les deux. Nombreux cas possibles. Par exemple 6 x 4 est divisible par 2 et par 3.
Conclusion	Pas de piste sérieuse!

Test et erreurs – Objectif 87

On "apprivoise" la formule en remplissant les chiffres dans l'ordre

ascendant puis

descendant.
Résultats inférieurs au 87 cherché.

On va donc procéder par approximations successives.

1 + 8,66 + 58 + 6,22 = 73,88

9 + 14,86 + 62 + 6 = 68

On cherche à obtenir des entiers avec les fractions

(ce qui n'est pas une obligation pour la solution).

9 + 26 + 35 + 14 = 84 au lieu de 87

Inversion de deux valeurs pour augmenter le résultat

9 + 26 + 37 + 14 = 86 au lieu de 87

Agissons sur les facteurs 12 et 13 pour encore augmenter le résultat

9 + 39 + 25 + 14 = 87 BINGO

Une des solutions

(15^e avant la fin dans la liste du tableau des solutions).

Un exemple de solution avec fractions non entières

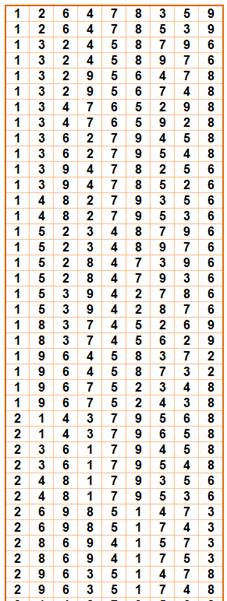
Cette solution est la première listée dans le tableau: elle est notée:

1 2 6 4 7 8 3 5 9

1 + 4,33 + 80 – 11 +1,66 – 10 = 65,99

Quantité de solutions

La rechercher systématique peut se faire soit sur tableur, un peu fastidieux, ou avec une programme si on dispose de cette facilité.

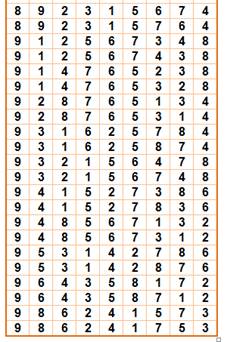
Quantité de possibilités:

9 possibilités pour a

8 possibilités pour b, car a en prend 1

7 possibilités pour c

etc.

Soit un total égal à factoriel 9.

En tenant compte des permutations:

Q = 9! / 4 = 90 720

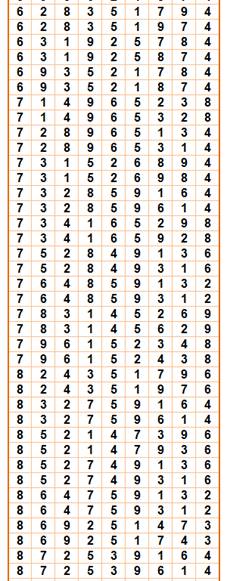
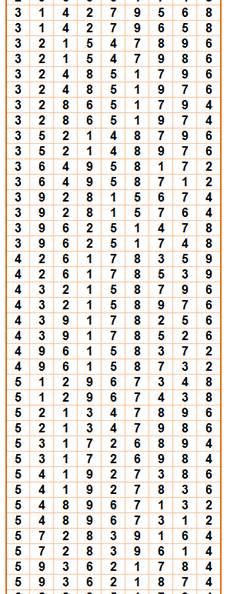
Tableau des 136 solutions (soit 136 / 4 = 34 solutions primitives)

Presse de mai 2015

De nombreux journaux ont relayé cette information dont l'origine serait le Guardian à partir de VN Express (journal du Vietnam)):

Ce puzzle arithmétique a été proposé à des enfants de 8 ans d'une école vietnamienne Niveau CE2.

En français, les articles sont intitulés: saurez-vous résoudre ce puzzle mathématique donné aux Vietnamiens de 8 ans?

Les problèmes récents présentés par la Presse de 2015

L'anniversaire de Cheryl – Problème soumis à des élèves de Singapour dans le cadre d'une olympiade de mathématiques (avril 2015).
Calcul du serpentin arithmétique posé aux élèves de CE2 vietnamiens (mai 2015).
Le crocodile et le zèbre – Énigme posée lors d'un examen à des lycéens écossais (octobre 2015
Les pommes bananes et noix de coco – Quatre égalités avec une inconnue
Priorité des opérations et division par une fraction