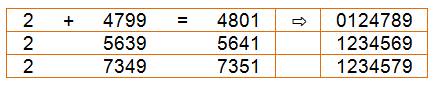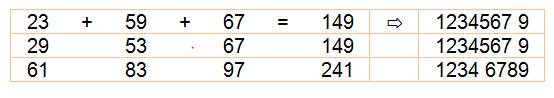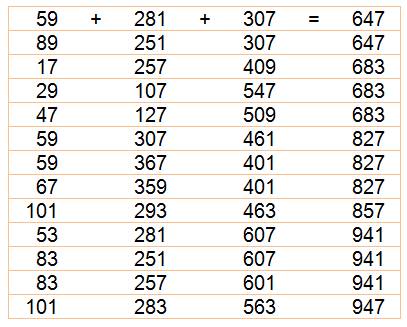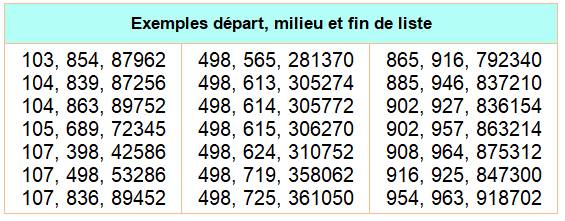
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/12/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Jeux avec Chiffres
Débutants Chiffres	Pannumériques		Glossaire Chiffres
INDEX Jeux Motifs	Pannumérique	Somme
		Sommaire de cette page Addition pannumériques à >>> Deux termes >>> Trois >>> Quatre >>> Multiplication et division pannumériques

Sommes de premiers

pannumériques

Quelles sont les additions de nombres premiers avec somme premières utilisant le maximum de chiffres différents et si possibles tous.

Par exemple: avec 2 + 17 = 19, les trois nombres sont premiers et les chiffres employés sont: 1, 2, 7 et 9. C'est la plus petite telle addition avec quatre chiffres différents.

Addition pannumérique à deux termes
La somme (s) de deux nombres (a et b) implique trois nombres (s = a + b) et k chiffres parmi les dix possibles. Les trois nombres (a, b, c) sont premiers. Quelles sont les sommes qui produisent le plus de chiffres différents (seuls ou multiples)? Parmi toutes les sommes pour a et b jusqu'à 100, deux remarques: maximum quatre chiffres utilisés, et seul a = 2 engendre notre somme Pas étonnant, tous les autres nombres premiers sont impairs et leur somme est naturellement paire. Il faut b > 4 000 pour atteindre une somme comportant 7 chiffres différents et 30 000 pour huit chiffres.	Toutes les sommes jusqu'à 100 Sept chiffres jusqu'à 10 000 Huit chiffres

Addition pannumérique à trois termes
Avec trois termes inférieurs à 100, trois additions sont quasi-pannumériques. Notez qu'il n'y a aucun 0. Il ne faut aller beaucoup plus loin pour atteindre la pannumérique. La plus petite addition de premiers avec somme première contenant tous les chiffres de 0 à 9 est: 59 + 281 + 307 = 647.	Toutes les sommes jusqu'à 100 Pannumériques

Addition pannumérique à quatre termes

La plus petite somme jusqu'à 100 Avec trois termes inférieurs à 100, la plus petite addition comportant le maximum de chiffres est celle indiquée. Évidemment, on recommence avec la nécessité d'un 2 parmi les termes de l'addition pour que la somme soit impaire et susceptible d'être première. Pannumériques La plus petite somme pannumérique à quatre termes avec des premiers est 409 avec seulement deux chiffres doublés (1 et 7). Avec un seul chiffre doublé, on autait:

Multiplication et division

Nous cherchons le produit le plus petit dont la multiplication est pannumérique. Plus question de mettre une restriction avec des premiers. Le produit est naturellement composé. Il existe de nombreuses multiplications pannumériques à 10 chiffres. Les plus petites divisions avec chiffres différents Voici enfin des nombres pannumériques stricts, avec les dix chiffres une seule fois (rouge). Trois exemples.

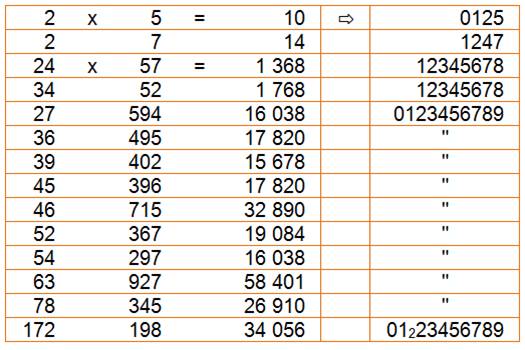
Voir suite Produits pannumériques

Suite	Somme de chiffres en puissance
Voir	Allumettes et nombres Bases de numération Chiffres et puissances Nombres en toutes lettres Numération - historique Pannumérique
DicoNombre	Nombre 27 Nombre 409 Nombre 677 Nombre 809 Nombre 16 038
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/SomPrem.htm