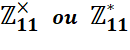Logarithme discret ou modulaire

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/12/2018 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Analyse
Débutants Logarithme	LOGARITHME				Glossaire Général
INDEX Analyse	Introduction	Calcul	Exemples	Changement de base
	Log et unités	Propriétés	Décibel	EXPONENTIELLE
	Log Discret	Table	Maths	Historique
		x . ln(x) …	ln(x + 1) < x
		Sommaire de cette page >>> Approche >>> Logarithme discret >>> À retenir >>> Définition >>> Table de valeurs

LOGARITHMES DISCRETS

Logarithmes modulaires

Une manière d'obtenir des valeurs logarithmiques en nombres entiers. Possibilité atteinte au prix d'une restriction du champ de travail, limité aux nombres de 1 à p, un nombre premier (monde modulaire).

Une opération dont le calcul est simple dans un sens et nettement plus compliquée dans l'autre. Propice aux applications en cryptographie (protocole Diffie-Hellman, cryptosystème ElGamal).

Anglais : Discrete logarithm / Modular logarithms

Approche

Logarithmes et exponentielles (rappels)

Les mondes des logarithmes et des exponentielles sont liés (fonctions réciproques).

Notre ambition

Il est rare qu'un logarithme, quelle que soit la base (10, 2 , e …) soit un nombre entier.

Quelle est la manière d'en faire des nombres entiers ?

Logarithmes ordinaires

log₂ 8 = 3

log₂ 5 = 2,321928094…

Logarithme entier

Existe-t-il un nombre entier n tel que:

log₂ 5 = n entier ?

Adapter le terrain de jeu

Il faut redéfinir le terrain de jeux. Au lieu de prendre tous les entiers, on se limite, par exemple aux nombres de 0 à 11. Comme on se limite à 12 pour les heures sur l'horloge.

En pratique, on ne retient que les restes de la division par 11; on dit que l'on calcule modulo 11.

Le terrain de jeu est nommé:

Avec Z, l'ensemble des nombres relatifs.

Le logarithme discret tire son nom du fait qu'il opère dans cet ensemble fini.

Anglais: discrete logarithm under modular arithmetics.

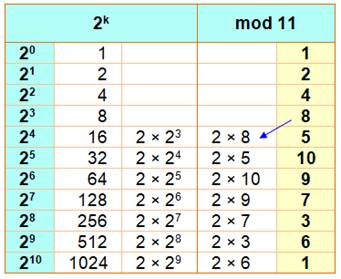
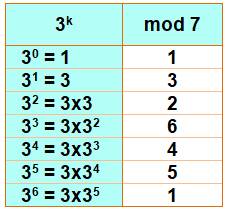
Calcul des restes de la division par 11 des puissances de 2

Notez la présence de tous les nombres de 1 à 10. Notez également comment calculer les restes (mod) à partir de 8: on se base sur les résultats déjà connus.

Lecture du tableau pour l'exemple vu ci-dessus.

Notez que, comme nous l'avions vu, ici, pas besoin de calcul modulo: le résultat est compris entre 0 et 10.

Appliquons procédure modulo pour 2⁴.

Cette fois nous avons aussi, une valeur entière, mais en restreignant notre terrain de jeu aux nombres de 0 à 10.

Dans le monde (modulo 11)

Logarithme discret
Pour définir un logarithme discret, on restreint le terrain de jeu: de 0 à p – 1, avec p un nombre premier.		Dit groupe multiplicatif modulo le nombre premier 11.
Avec notre exemple: le logarithme discret de 5 en base 2 dans le groupe Z₁₁ est 4.
Autre exemple dans Z₁₁
Dans Z₅		log₂ 1 = 0 log₂ 2 = 1 log₂ 3 = 3 log₂ 4 = 2 log₂ 5 n'existe pas On note les valeurs successives: 5, 2, [ 0, 1, 3, 2 ] Avec: 5 pour Z₅ et 2 pour log₂,
Dans Z₁₁ Dans Z₁₃	11, 2, [0, 1, 8, 2, 4, 9, 7, 3, 6, 5] 13, 2, [0, 1, 4, 2, 9, 5, 11, 3, 8, 10, 7, 6] Ex:
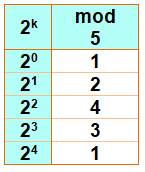
Dans Z₇ & Base 2 Dans Z₇, seuls les log₂ de (1,2 et 4) sont définis. 7, 2, [0-3, 1-4, x, 2-5, x, x] On ne retient que les plus petites valeurs: 7, 2, [0, 1, x, 2, x, x]			Dans Z₇ & Base3 En revanche, les log₃ sont tous définis. 7, 3, [0, 2, 1, 4, 5, 3] Dans ce cas, le groupe Z₇ avec générateur 2 est cyclique.

À retenir

Définition

Voir Groupe cyclique

Tables de valeurs
Base 2	3, 2, [0, 1] 5, 2, [0, 1, 3, 2] 7, 2, [0, 1, x, 2, x, x] 11, 2, [0, 1, 8, 2, 4, 9, 7, 3, 6, 5] 13, 2, [0, 1, 4, 2, 9, 5, 11, 3, 8, 10, 7, 6] 17, 2, [0, 1, x, 2, x, x, x, 3, 7, x, x, x, 6, x, 5, 4] 19, 2, [0, 1, 13, 2, 16, 14, 6, 3, 8, 17, 12, 15, 5, 7, 11, 4, 10, 9] 23, 2, [0, 1, 8, 2, x, 9, x, 3, 5, x, x, 10, 7, x, x, 4, x, 6, x, x, x, x] 29, 2, [0, 1, 5, 2, 22, 6, 12, 3, 10, 23, 25, 7, 18, 13, 27, 4, 21, 11, 9, 24, 17, 26, 20, 8, 16, 19, 15, 14] 31, 2, [0, 1, x, 2, x, x, x, 3, x, x, x, x, x, x, x, 4, x, x, x, x, x, x, x, x, x, x, x, x, x, x] Note: la valeur x dans la liste indique que le log de ce rang n'est pas défini. Ex: Dans Z₇ on a [0, 1, x, 2, x, x] => log₂ (3, 5 et 6) ne sont pas définis. Les groupes cycliques multiplicatifs sont signalés en rouge.
Base 3	5, 3, [0, 3, 1, 2] 7, 3, [0, 2, 1, 4, 5, 3] 11, 3, [0, x, 1, 4, 3, x, x, x, 2, x] 13, 3, [0, x, 1, x, x, x, x, x, 2, x, x, x] 17, 3, [0, 14, 1, 12, 5, 15, 11, 10, 2, 3, 7, 13, 4, 9, 6, 8] 19, 3, [0, 7, 1, 14, 4, 8, 6, 3, 2, 11, 12, 15, 17, 13, 5, 10, 16, 9] 23, 3, [0, 7, 1, 3, x, 8, x, 10, 2, x, x, 4, 5, x, x, 6, x, 9, x, x, x, x] 29, 3, [0, 17, 1, 6, 10, 18, 8, 23, 2, 27, 5, 7, 26, 25, 11, 12, 21, 19, 13, 16, 9, 22, 4, 24, 20, 15, 3, 14] 31, 3, [0, 24, 1, 18, 20, 25, 28, 12, 2, 14, 23, 19, 11, 22, 21, 6, 7, 26, 4, 8, 29, 17, 27, 13, 10, 5, 3, 16, 9, 15] 37, 3, [0, x, 1, 7, x, x, 4, x, 2, 12, 15, 8, x, x, x, 14, x, x, x, x, 5, x, x, x, 17, 6, 3, 11, x, 13, x, x, 16, 10, x, 9]
Base 4	5, 4, [0, x, x, 1] 7, 4, [0, 2, x, 1, x, x] 11, 4, [0, x, 4, 1, 2, x, x, x, 3, x] 13, 4, [0, x, 2, 1, x, x, x, x, 4, 5, x, 3] 17, 4, [0, x, x, 1, x, x, x, x, x, x, x, x, 3, x, x, 2] 19, 4, [0, x, x, 1, 8, 7, 3, x, 4, x, 6, x, x, x, x, 2, 5, x] 23, 4, [0, 6, 4, 1, x, 10, x, 7, 8, x, x, 5, 9, x, x, 2, x, 3, x, x, x, x]
Base 5	7, 5, [0, 4, 5, 2, 1, 3] 11, 5, [0, x, 2, 3, 1, x, x, x, 4, x] 13, 5, [0, x, x, x, 1, x, x, 3, x, x, x, 2] 17, 5, [0, 6, 13, 12, 1, 3, 15, 2, 10, 7, 11, 9, 4, 5, 14, 8] 19, 5, [0, x, x, 8, 1, 2, 6, x, 5, x, 3, x, x, x, x, 7, 4, x] 23, 5, [0, 2, 16, 4, 1, 18, 19, 6, 10, 3, 9, 20, 14, 21, 17, 8, 7, 12, 15, 5, 13, 11] 29, 5, [0, x, x, 9, 1, 13, 12, x, 3, x, x, x, 11, x, x, 4, x, x, x, 10, x, 5, 6, 8, 2, x, x, 7] 31, 5, [0, x, x, x, 1, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, 2, x, x, x, x, x] 37, 5, [0, 11, 34, 22, 1, 9, 28, 33, 32, 12, 6, 20, 13, 3, 35, 8, 5, 7, 25, 23, 26, 17, 21, 31, 2, 24, 30, 14, 15, 10, 27, 19, 4, 16, 29, 18] 41, 5, [0, 3, x, 6, 1, x, x, 9, 5, 4, x, x, x, x, x, 12, x, 8, x, 7, 17, x, 18, x, 2, x, x, x, x, x, 14, 15, 19, x, x, 11, 16, x, 13, 10]
Base 7	11, 7, [0, 3, 4, 6, 2, 7, 1, 9, 8, 5] 13, 7, [0, 11, 8, 10, 3, 7, 1, 9, 4, 2, 5, 6] 17, 7, [0, 10, 3, 4, 15, 13, 1, 14, 6, 9, 5, 7, 12, 11, 2, 8] 19, 7, [0, x, x, x, x, x, 1, x, x, x, 2, x, x, x, x, x, x, x] 23, 7, [0, 14, 2, 6, 7, 16, 1, 20, 4, 21, 19, 8, 10, 15, 9, 12, 5, 18, 17, 13, 3, 11] 29, 7, [0, x, x, x, x, x, 1, x, x, x, x, x, x, x, x, 5, x, x, x, 2, x, x, 4, 3, 6, x, x, x] 31, 7, [0, 3, x, 6, 5, x, 1, 9, 14, 8, x, x, x, 4, x, 12, x, 2, 13, 11, x, x, x, x, 10, x, x, 7, x, x] 37, 7, [0, x, x, x, x, x, 1, x, 5, 3, x, 2, x, x, x, 8, x, x, x, x, x, x, x, x, x, 6, x, x, x, x, x, x, 4, 7, x, x] 41, 7, [0, 14, 25, 28, 18, 39, 1, 2, 10, 32, 37, 13, 9, 15, 3, 16, 7, 24, 31, 6, 26, 11, 4, 27, 36, 23, 35, 29, 33, 17, 12, 30, 22, 21, 19, 38, 8, 5, 34, 20] 43, 7, [0, x, x, x, x, 2, 1, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, x, 4, 5, x, x, x, x, 3]

Retour	Logarithme
Suite	Logarithmes – Calcul Logarithmes et tout nombre
Voir	Arrondis avec logarithmes Calcul des factorielles avec les logs Croissance Constantes Mathématiques Courbes élémentaires Exponentielle Exposants – Index Exposants et puissances Les 17 équations qui ont changé le monde
Sites	Le « problème du logarithme discret » en cryptographie – Christophe Delaunay – CNRS – 2015 What is the difference between discrete logarithm and logarithm – Cryptography Discrete logarithm calculator – Apertron.com
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/LogDiscr.htm