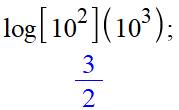NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/09/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Analyse
Débutants Logarithme	LOGARITHME				Glossaire Général
INDEX Analyse	Introduction	Calcul	Exemples	Changement de base
		Propriétés	Décibel	EXPONENTIELLE
		Table	Maths	Historique
		Sommaire de cette page >>> Changement de base >>> Calcul – Exemples >>> Travaux pratiques >>> Exemple de calcul avec chnagement de base >>> Variations sur log >>> Logarithme et Maple

LOGARITHMES

Changement de base / Conversion

Comment passer d'une base de logarithme à une autre. Notamment des logarithmes népériens aux logarithmes décimaux.

Réciprocité des fonctions logarithmes et exponetielles:

Anglais : The logarithm of x to the base a

The logarithm of the base itself is 1

CHANGEMENT DE BASE
Changement de base Formule base quelconque Formule base décimale (a = 10) et népérienne (b = e = 2,718182...)

Voir Types de logarithmes / Constante e

Explications
	Base a		Base b
Soit le log en base a à exprimer en base b	loga N	= L
Ce qui veut dire que (fonction réciproque)	N	= a^L
Reprenons en base b			logb N
Remplaçons N par sa nouvelle valeur				= logb a^L
Propriété des log				= L . logb a
Soit la valeur de L			L	= logb N / logb a
Et, la passerelle entre les deux bases	loga N			= logb N / logb a

Exemple de calcul
Ma table (ma calculette) me donne bien les logarithmes népériens (ln base e = 2,718…), mais je cherche un nombre dont je ne connais que le logarithme décimal (log base 10). Comment s'y prendre? Exemple: calculer 100 x 1000 avec les logarithmes (Exemple volotairement simpliste pour se concentrer sur la méthode)
A = 100 B = 1000 P = A . B	log A = 2 log B = 3 log P = log A + log B log P = 2 + 3 = 5
P = ?		Dans ce cas simple évidemment log 5 donne 100 000. Mais supposons que ce nombre soit plus compliqué. Que vaut P? Sachant que nous sommes en base 10. Et que nous n'avons que la table de la base "e" disponible.
	log P = ln P / ln 10 ln P = log P . ln 10			Changement de base selon la formule ci-dessus. On connaît logP on veut calculer ln10.
	log P = 5 ln 10 = 2,302585093…			On connaît la valeur du premier facteur Valeur de ln 10 selon notre table.
P = exp (log P x ln10) P = exp ( 5 x 2,30…) P = exp (11,51292546…)			Passage aux exponentielles (fonction réciproque du logarithme). On remplace log P par sa valeur connue.
P = 99 999, 99… = 100 000			Recherche de la valeur de cette exponentielle (table ou calculette).

TRAVAUX PRATIQUES
Base en racine Comment démontrer cette curiosité? Voici les outils en deux formules équivalentes: a^x= N loga N= x	Calcul avec retour aux puissances
Calcul de	Calcul avec changement de base
Calcul de	Calcul avec changement de base

Équation Il faut calculer x: 3^x – 1 . 5^2x – 1= 375 Voici les outils: log a^b= b . log a log(a.b) = log a + log b

Calcul La division de chaque côté par (log 3 + 2 log 5) est légitime car cette quatité est strictement positive.

Voir Nombre 2

Merci à Patrick Herrmann pour ses remarques

Exemple de calcul avec changement de base
Une expression en log pour x (x = logarithme de 2 en base 12) et une autre pour y (y = logarithme de 72 en base 6). Comment exprimer y en fonction de x ? D'abord effectuer un changement de base.

Voir Brève 725

VARIATIONS sur les LOG

Logarithme et Maple
Le calcul littéral impliquant des logarithmes sur un logiciel de calcul symbolique comme Maple nécessite de petites précautions. En effet, le logarithme n'est pas défini avec des nombres négatifs (sauf avec des nombres complexes).
		Ces instructions avec "assume" (supposez en anglais) indique au programme que les nombres a, n et m sont positifs tout au long des calculs. [a] indique qu'il s'agit d'un logarithme en base a. La réponse est n avec une tilde (~) qui indique que ce nombre est lié à des hypothèses. La base doit être un nombre sans puissance (pourquoi?). Pour contourner cette interdiction, on calcule préalablement la base (ici en a²) La réponse est 3/2 avec le 3 de la puissance du nombre et le 2 de la puissance de la base.
Quelques valeurs

Identités pratiques pour n > 1

Voir Solution universelle au problème des quatre 4

Suite	Logarithmes – Calcul Logarithmes – Historique Balle qui rebondit Logarithmes et tout nombre Changement de base en exponentielle
Voir	Arrondis avec logarithmes Calcul des factorielles avec les logs Croissance Constantes Mathématiques Courbes élémentaires Échelle de Richter Exponentielle Exposants – Index Exposants et puissances Morphisme
DicoNombre	Nombre 1 Ln 2 = 0,693… Ln 10 = 2,302 …
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/Logabase.htm