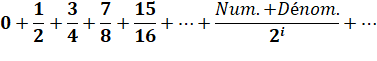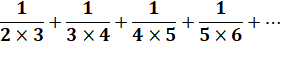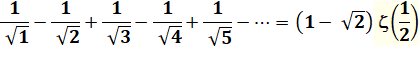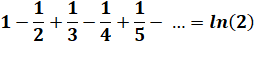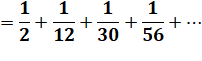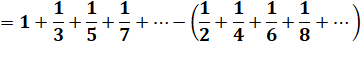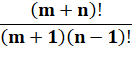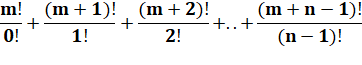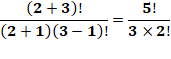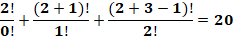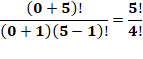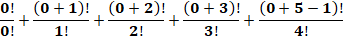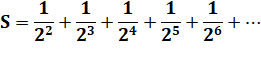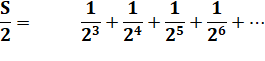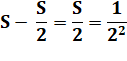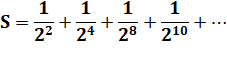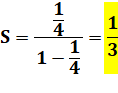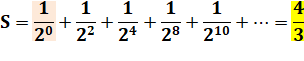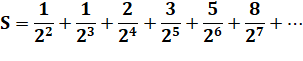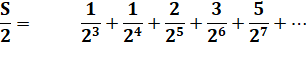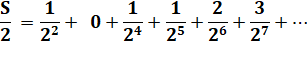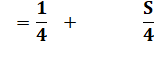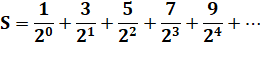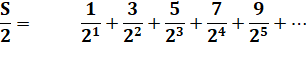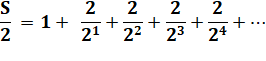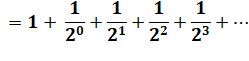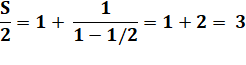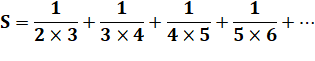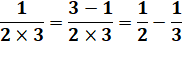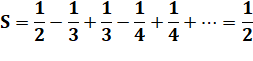|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Suites et séries
typiques
|
1 |
|
|
0,5 |
Voir Calcul |
|
0,604489 … |
Voir Fonction
zêta |
|
0,693147… |
Ces deux
dernières suites sont divergentes, ce qui donnerait "infini moins
infini" = indéterminé. Voir Somme alternée des inverses des
entiers / Log2
et ln2 |
![]()
Factorielles transformées en somme
|
|
|
|
|
|
|
|
|
Voir Factorielles
![]()
Calculs de Suites
infinies (infinite sums)
|
|
||
|
Valeur de cette
série: |
|
|
|
Valeur de sa
moitié: |
|
|
|
Différence: |
|
|
|
Valeur de la
suite infinie: |
|
|
|
Variante en
ajoutant 1/2 |
|
|
Voir Puissances
de 2
|
|
||
|
Valeur de cette
série: Exemple d'une des premières séries calculées dans
l'histoire. Calcul réalisé par Archimède
vers 220 av. J.-C. |
Progression
géométrique de raison ¼
|
|
|
Démonstration muette avec les
carrés Un grand carré
de côté unité. Son aire est également égale à 1. Le carré jaune représente un quart de la surface,
le suivant, un quart de la précédente, etc. La zone jaune représente notre
série. Les zones jaune, bleue et verte représentent
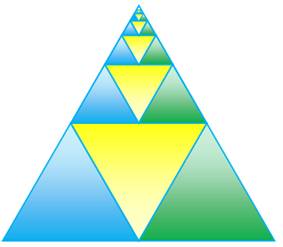
chacune notre série. 3S = 1 Démonstration muette avec les
triangles équilatéraux Un grand triangle équilatéral
d'aire unité, divisé en quatre
triangles équilatéraux. L'aire de chacun est égale à ¼ de celle du grand. Les zones représentent chacune notre série,
divisant l'aire unité en trois. 3S = 1 |
|
|
|
|
||
|
Valeur de
cette série avec comme numérateur la suite de
Fibonacci: |
|
|
|
Valeur de
sa moitié: (Méthode assez classique de calcul d'une suite infinie) |
|
|
|
Différence
qui vaut S/2: |
|
|
|
Valeur de
la suite infinie: |
S = 1 |
|
|
|
||
|
Valeur de
cette série avec comme numérateur les nombres impairs |
|
|
|
Valeur de
sa moitié: |
|
|
|
Différence
qui vaut S/2: |
|
|
|
|
||
|
Valeur de
la suite infinie: |
S = 6 |
|
|
|
||
|
Limite
de: |
|
|
|
On
utilise cette propriété: |
|
|
|
En
remplaçant: |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()