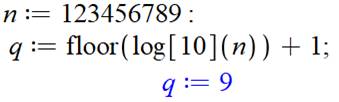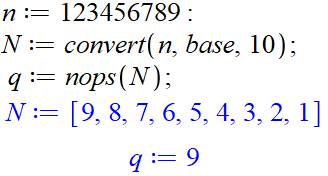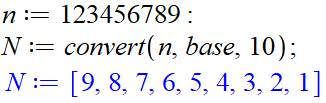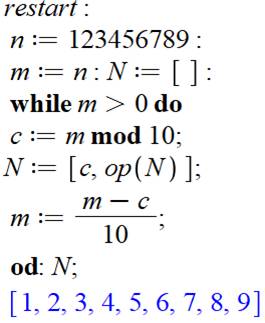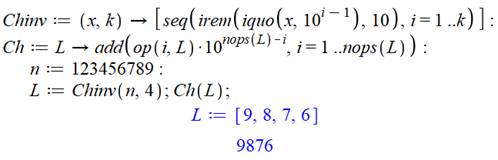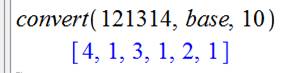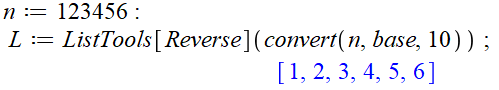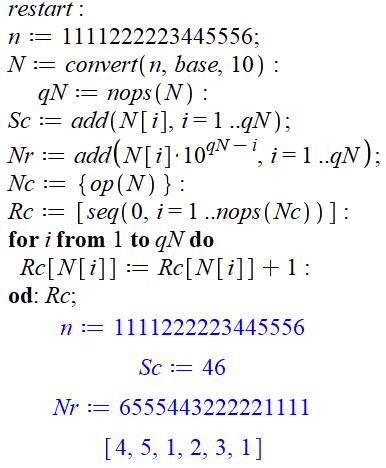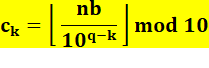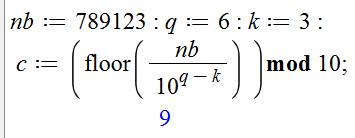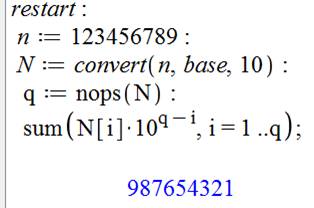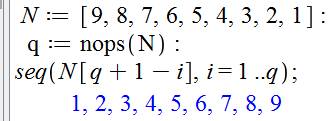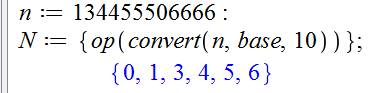|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Extraire les chiffres d'un nombre et les retourner Plusieurs possibilités: |
||
|
Pas à
pas Extraction des unités puis des
dizaines, etc. Programmation la plus simple
possible. À voir comme exercices de programmation. |
Algébrique Extraction directe par évaluation
d'une expression algébrique (une formule). Programmation avec instructions
avancées de sommation. |
Instruction
dédiée Extraction par conversion en base 10. Programmation avec instructions
prévues pour (dédiées). |
|
|
||
|
Calcul du logarithme en base 10 du
nombre; Prendre la partie entière
(floor = plancher);
et Ajouter 1 |
|
|
|
On pourrait être tenté de
dire qu'il est inutile de faire +1, il suffirait de prendre la fonction
plafond (ceil). Ça ne marche pas pour les
puissances de 10. |
|
|
|
Avec la conversion en liste,
obtenue avec Maple en réalisant une conversion en base 10. L'instruction nops (nombre
d'éléments) indique la quantité de chiffres. |
|
|
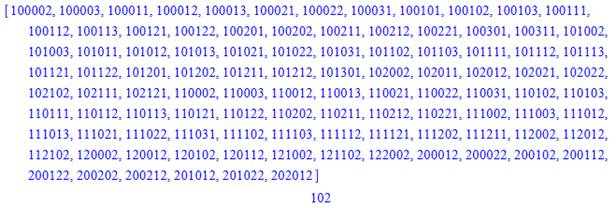
Voir Quantité de
chiffres k pour compter de 1 à n
|
|
|||
|
Direct Avec la
conversion en liste, obtenue avec Maple en réalisant une conversion en base
10. |
|
||
|
Par calcul En
"épluchant" le nombre chiffre par chiffre. Soit le
nombre n que nous plaçons dans m une variable de travail. La liste N des
chiffres est initialisée. Pendant
que m reste positif, le dernier chiffre de m est isolé avec la fonction mod 10. Ce
chiffre est placé dans la liste, tous en conservant les valeurs déjà
présentes par op(N). La
variable m est mise à jour en lui supprimant le chiffre qui vient d'être
traité En bleu,
le résultat du traitement. |
|
||
|
Par calcul et instruction compacte
|
Comment former un nombre inversé avec les k
derniers chiffres d'un nombre ? Chinv extrait les k
derniers chiffres et Ch reforme le nombre avec ces chiffres. |
||
|
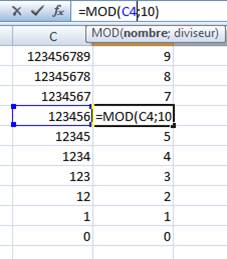
Avec un tableur Même
principe de calcul que ci-dessus. En
colonne C, le nombre de plus en plus grignoté en prenant la différence (C –
D), divisée par 10. En conne
D, extraction du dernier chiffre par mod 10. Autant de
lignes que nécessaire pour atteindre 0 dans C. Voir Méthode par formulation directe |
|
||
Voir Algorithme itératif de
Kaprekar
|
|
|||
|
Avec
Maple, et sans doute avec la plupart des logiciels mathématiques, on obtient
immédiatement les chiffres d'un nombre en faisant une conversion à base 10. |
|
||
|
Comment
remettre les chiffres dans le bon ordre? Voici un
programme mettant en œuvre deux conversions en base 10 . (voir optimisation plus bas). La liste N contient donc les chiffres du nombre
nb, mais à l'envers. On calcule son retourné r en prenant chacun des
chiffre trouvé N[i] multiplié par la puissance 10 correspondant à son rang
dans le retourné (q –i). Il suffit de convertir à nouveau en base 10 pour
obtenir la liste des chiffres dans l'ordre ordinaire. Note: On aurait pu créer directement la nouvelle
liste NN à partir de N. Pas plus simple. |
|
||
|
Mieux
avec le logiciel ListTool. |
|
||
Voir Nombres de Keith – Programme
|
|
||
|
|
Commentaires Initialisation générale (sage précaution!) Introduction manuelle du nombre à traiter. Conversion en base 10 pour disposer des chiffres
dans la liste N avec qN la quantité de chiffres. La somme des chiffres
est calculée en Sc. Le nombre retourné
de n est mis en Nr. Pour calculer la quantité
de chiffres de chaque sorte: On place les chiffres dans l'ensemble Nc (ici, on
aura l'ensemble {1, 2, 3, 4, 5, 6}, soit chaque chiffre de n représenté une seule fois. On initialise à 0, un compteur Rc de la taille de
l'ensemble des chiffres (nops(Nc)). On va y compter la quantité de chiffres de chaque
sorte. Si le chiffre de N est 3, par exemple, alors on ajoute 1 en troisième
position du compteur Rc. En bleu, les résultats des traitements. |
|
Voir Calcul des nombres jonctions
|
|
||
|
Formule L'idée
serait d'avoir une formule qui calcule directement les chiffres. Elle existe. Le kième chiffre d'un nombre nb de q chiffres est
égal au reste de la division par 10 (mod 10) de l'arrondi par le bas
(plancher) du nombre divisé par 10 à la puissance (q-k). Le rang k étant compté de 1 à k de gauche à
droite. |
La puissance (q – k) s'explique du fait que les puissances de 10 vont
croissant vers la gauche. Les crochets vers le bas signifient que l'on ne conserve que l'entier
en éliminant les virgules (valeur-plancher
ou floor en anglais). |
|
|
Recherche d'un chiffre Application
de la formule On divise le nombre par la puissance de 10
correspondant à la position (q – k) du chiffre cherché . |
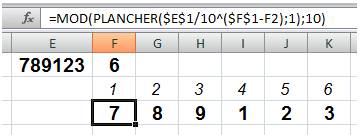
Le 3e chiffre de 789 123, un nombre à q = 6 chiffres, est
9. |
|
|
Quantité de chiffres Comment éviter d'avoir à préciser la
quantité de chiffres (q) Le logarithme en base 10 va servir. En effet:
D'où la formule: q est l'entier + 1 obtenu en
prenant le log 10 du nombre. |
La quantité de chiffres du nombre n est égale à la valeur-plancher
(floor) de la valeur (evalf) du logarithme base 10 de n, plus 1. |
|
|
Formulation sur tableur En F1 => =PLANCHER(LOG(E1);1)+1 En F3 =>
=MOD(PLANCHER($E$1/10^($F$1-F2);1);10) |
|
|
|
Liste des chiffres Comment obtenir automatiquement toute la
liste des chiffres. On calcule le nombre q de chiffres. Puis, on lance la création d'une liste (séquence)
pour k de 1 à q, chaque nombre de la liste est un chiffre du nombre calculé
comme ci-dessus. |
L'instruction seq calcule la fonction indiquée et cela pour chacune
des valeurs de k de 1 à q. |
|
|
|
||
|
Le retourné d'un nombre est ce nombre
avec tous les chiffres dans le sens inverse. Si l'on dispose de l'instruction de conversion,
le calcul est immédiat. Comme l'instruction seq, l'instruction sum
calcule chacune des valeurs pour i de 1 à q. En plus elle le somme |
Le nombre est transformé en liste et la somme pondéré par les puissance
de dix donne le nombre retourné. |
|
|
Recherche de palindromes Il suffit
de tester l'égalité entre le nombre n et son retourné r. |
|
|
|
Retournement d'une liste Le moyen
le plus simple pour inverser l'ordre des nombres dans une liste. |
|
|
|
Extraction rapide des chiffres il s'agit
d'extraire les chiffres d'un nombre dans une liste et dans le bon ordre. |
|
|
|
|
|||
|
|
Voir Nombres carrément
réversibles Recherche On cherche les nombres tel que
Procédure On implante le programme vu ci-dessus dans une procédure nommée
Retour. Sorte de nouvelle instruction qui calcule le retourné d'un nombre. Programme Le programme de recherche appelle cette procédure Retour pour le
retourné de n² et aussi pour le retourné de n que l'on porte au carré. Sortie de n si ces deux nombres
sont égaux. On a pris la précaution d'éliminer les nombres divisibles par 10
(terminés par des 0) et aussi ceux qui doublonnent comme 201 pour 102. Les valeurs de n qui répondent au critère sont placées dans la liste
L. Le compteur kt indique la quantité de cas trouvés. Pour n de 100 à 150, le programme indique huit valeurs. Exemple: 122² = 14884
221² = 48841 5 cas dont 8 comportant le chifre3 |
||
|
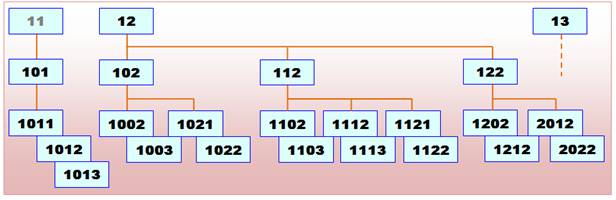
Les trois pères de famille
|
Les nombres pilotes sont 11, 12 et 13, tous les autres en découlent en
intercalent 0, 1,2 ou 3. |
||
|
|
de 10 000 à 100 000 8 fois le chiffre 3 |
||
|
|
de 100 000 à 1 000 000 20 fois le chiffre 3 |
||
|
|
de 1 000 000 à 10 000 000 Ils sont 491 entre 10 millions et 100 millions. Le chiffre 3 se fait de plus en plus rare. |
||
Merci à Georges Vidiani
et à Michel L. pour leurs contributions
|
|
||
|
Comment identifier les types de
chiffres présents? La conversion en base 10 donne la liste des
chiffres. Sa conversion en un ensemble ne retient qu'un
représentant de chaque chiffre. |
Les { } demandent un ensemble et op permet de sélectionner tous les
éléments de la liste. |
|
|
Quantité de chiffres de chaque type Le premier nombre de la liste Q donne la quantité de 0, puis celle
de 1, etc. On examine chaque nombre ni Si n vaut 3, par exemple, on ajoute 1 au
quatrième nombre dans Q, celui qui indique la quantité de 3 dans le nombre. |
|
|
Voir Redondance
pour comparaison avec les chiffres
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()