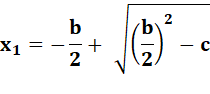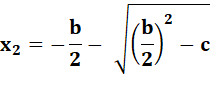|
|||||||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS du 2e degré ou Équation quadratique L'équation
du deuxième degré possède deux racines, réelles
ou complexes. Comment les
calculer? S'il vous plait, la solution, tout de
suite! >>>
|
|
|
||
|
Équation: |
x²
+ bx + c = 0 |
|
|
L'idée
consiste à transformer le début de l'équation en un carré. |
x² + 2kx + k² = (x + k)² |
|
|
Pour
obtenir la ressemblance sur les deux premiers termes, nous devons écrire: |
b = 2k k = b/2 |
|
|
Remplaçons.
Il
est bien tentant de remplacer le début de cette équation par sa valeur. De
sorte que le seul x qui reste est sous une expression au carré. |
x² + bx + (b/2)² = (x + b/2)² –
c + (b/2)² =
(x + b/2)² (x + b/2)² = (b/2)² – c |
|
|
Posons
R² la valeur du carré: Et
ses deux racines: Soit
les deux valeurs de x: |
(x + b/2)² = R² = (b/2)² – c x1 + b/2 = R ou x2 + b/2 = – R x1 = R – b/2 ou x2
= – R – b/2 |
|
|
En
redéveloppant et sous la forme habituelle: |
|
|
|
Exemple |
|
|
|
Équation: |
x²
– 2x – 8 = 0 |
|
|
Expression
sous radical (b/2)² – c |
(–2/2)² + 8 = 9 = 3² |
|
|
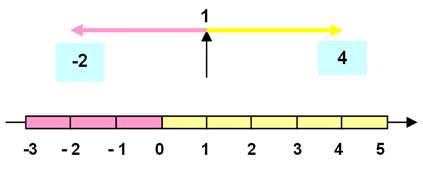
Racines |
x1 = 2/2
+ 3 = 4 x2 = 2/2
– 3 = – 2 |
|
|
Illustration Racines symétriques autour du pivot - b/2 = 2/2 = 1
|
||
|
|
||
|
Équation
(a On
divise d'abord par a. L'idée
est la même que celle indiquée ci-dessus, en revenant au cas a = 1. Il
s'agit de dégager un carré avec x et de laisser un terme constant. Pour cela
on ajoute une quantité adéquate que l'on soustrait aussitôt. Avec
les trois premiers termes, formons un carré en utilisant une identité
remarquable classique. Donnons
les noms h et k aux quantités fractionnaires comme indiqué. À
partir de là, la résolution est simple. Il existe deux solutions: la racine
positive et la racine négative. Attention! Cette
extraction de racine n'est possible que si k² est positif. Et,
en remarquant que 4 a² est toujours positif, comme tout carré. Cette
expression est importante, puisqu'elle détermine si les racines existent ou
non. Elle
est appelée le discriminant de
l'équation et notée avec la lettre grecque delta. En
reprenant les coefficients d'origine (en vert), voici l'écriture des deux
racines, symétriques par rapport au nombre –b/2a. |
|
|
|
|
||
|
Rappel
sur le discriminant: Expression de c Revenons
aux racines et multiplions numérateur et dénominateur par la même quantité. |
|
|
Voir Déterminant / Forme canonique
|
|
|
|
Notez: si le discriminant est négatif, il n'y a pas de
racines; ce qui veut dire que la fonction ne coupe jamais l'axe des x. |
|
Voir Nombres
complexes et valeur de i / Résolution graphique / Complexes en terminales
|
|
|||
|
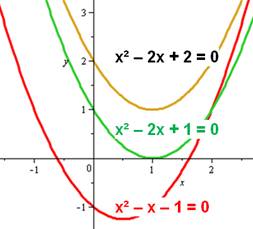
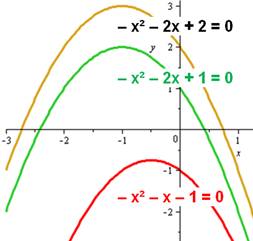
Exemple 1
|
x² – x – 1 = 0 |
x
= (1 Qui est le nombre d'or |
|
|
Exemple 2
|
x² – 2x + 1 = 0 |
qui
peut s'écrire: (x – 1)² = 0 et
a pour solution: x = 1. |
|
|
Exemple 3
|
x² – 2x + 2 = 0 |
x
= (2 = 1 |
|
|
Graphe de ces fonctions Le
graphe du haut présente les fonctions impliquées dans les équations.
Le
graphe du bas présente les mêmes fonctions mais avec x² en négatif (a = –1).
|
Que a de x² soit positif ou négatif, si le discriminant est négatif,
la courbe ne coupe pas l'axe des x; f(x) = ax² + bx + c n'a pas de racines. |
||
|
|
|
|
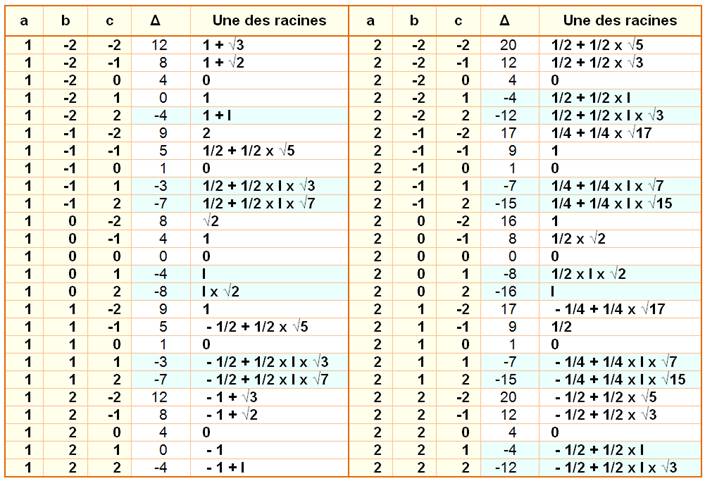
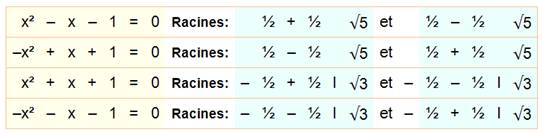
Quelques
équations résolues. En bleu, les racines complexes. Entraînez-vous
à calculer ces racines.
La
seconde racine se déduit de la première en inversant le signe du second
terme. Les solutions avec a
négatif se déduisent de ce tableau en inversant les signes. Exemples:
|
|
|
|
||
|
|
x² – 3x + 2 = 0 x² – 3x + 2 = (x – 1) (x – 2) |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()