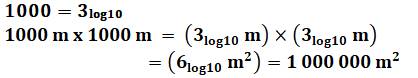|
||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Logarithmes et unités de mesure Quel est le rapport entre le
logarithme et les unités de mesures? Est-ce que l'unité est
affectée par le logarithme?
Le
logarithme est un nombre |
Rappels sur les nombres et les unités
|
Unité
des nombres: c'est le dernier chiffre à droite. Comme 5 dans 1 025. Unités
de mesure: elles accompagnent un nombre pour caractériser le type de
grandeur (longueur, masse, degré, intensité …). L'unité est appelée la dimension du nombre. Nombre sans dimension
c'est:
|
|
|
||
|
Le
logarithme d'un nombre est un nombre. Il est simplement exprimé sous une
autre forme que sa forme décimale habituelle. En effet,
un nombre peut être exprimé sous une diversité de formes selon les
applications. La forme
logarithmique d'un nombre est simplement une astuce pour faire côtoyer des
petits nombres avec de grands nombres. |
Exemple avec le nombre décimal 1000
|
|
|
|
|
|
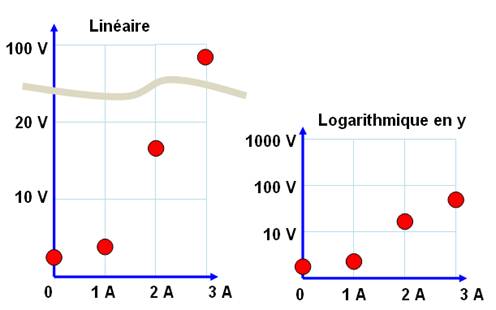
Il est parfois plus pratique de
montrer l'évolution d'une quantité en logarithmes pour ne pas avoir des
graphiques à rallonge, comme le montre cet exemple:
Il s'agit d'un mode de
représentation qui, vous le constatez sur les graphiques, n'a aucune
influence sur les unités utilisées À droite,
l'ordonnée (y) est en échelle logarithmique, mais ce sont toujours des volts
et, bien sûr, pas des logarithmes de volts.
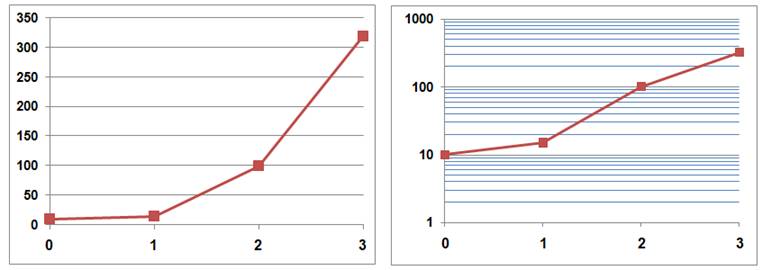
Seule
l'échelle des ordonnées a été transformée en échelle logarithmique. Si les
deux axes sont en présentation logarithmique, on parle d'échelle log-log. Attention, il ne s'agit pas d'un
tassement de l'axe des y. C'est un peu plus subtil. Voyez le quadrillage
horizontal sur ces graphiques représentant les mêmes données:
|
|
|
|
|||
|
Comme tout nombre, le logarithme
peut servir à exprimer la mesure d'une grandeur et alors, on le fait suivre
d'une unité. C'est le nombre qui est affecté par
le logarithme et certainement pas l'unité. On ne prend pas le logarithme de
l'unité de mesure (le logarithme de volts n'existe pas). Le
logarithme transforme le nombre, pas l'unité. C'est le cas de bien d'autres
transformations mathématiques (exponentielle,
sinus
…) |
Exemple 1 000 000 km = 6log10 km Mais cela fait
toujours des km et non des log de km. Comme on
pourrait dire avec les carrés: 1 000 000 = 1000²
km (ou
106 km) qui est
une longueur en km et non 1000² km² qui serait alors une surface exprimée en
km². |
||
|
Pourtant on multiplie bien les
mètres pour en faire des mètres-carrés? Alors … Parce que log (n) est un nombre, purement et
simplement. Prendre un
logarithme ne change pas la dimension de la grandeur. Le logarithme d'une pression reste une pression. S'il
existait log(Pa) serait une autre unité que le pascal (Pa). |
Exemple 1000 m x
1000 m = 1 000 000 m² = (1000 m)² Alors
pourquoi pas pour les log? En
représentation logarithmique
Notez
que:
|
||
Explication mathématique
|
Certains
veulent démontrer que les unités ne sont pas affectées par les logarithmes en
tenant un raisonnement mathématique.
Si
on s'avisait de prendre le logarithme des mètres (par exemple), on aurait un
résultat qui comporterait aussi des m2, des m3 …une
stupidité! |
|
|
||
|
Le champ d'application des
logarithmes concerne essentiellement les grandeurs qui ont une dynamique
importante et cependant on souhaite conserver une appréciation des petites
valeurs. |
Exemple en audio
pour respecter la sensibilité de notre oreille: il est très important de
conserver les nuances sur les sons faibles; par contre, on peut être moins
regardant sur les sons forts. Les amplificateurs audio (Dolby) se rapprochent
de cette représentation logarithmique. Exemple en traitement du
signal: en
général on cherche à révéler de petits signaux parmi le bruit, lequel peut
être important. Là aussi un traitement logarithmique peut être utile (outre
un traitement sur la fréquence (spectral) ou une exploitation de la loi de
probabilité du signal comparé à celle du bruit). |
|
|
|
||
|
Il est
plus courant d'utiliser le
logarithme d'un rapport, le dénominateur étant pris comme référence. C'est le
cas des bels
(B) et des décibels (dB) qui caractérisent un rapport de puissances. Si une
relation en physique comporte de tels rapports, il est avisé de rappeler les
dimensions pour les traiter correctement: |
Par exemple Comparons 1000 watts à 10 watts. Le rapport vaut 100, le logarithme base 10
vaut 2. Cela fait 2 bels ou 20 décibels.
Si dans un circuit, 10 W à l'entrée produisent
1000 W en sortie, le coefficient d'amplification en puissance est de 100. On dit plutôt qu'il s'agit d'un
amplificateur de 20 dB. |
|
|
Le logarithme est une manière de
représenter un nombre. Ce n'est en aucun cas une unité en soi. Il peut être accompagné d'une unité
comme tout nombre et alors l'unité est conservée telle quelle. On l'utilise couramment en physique
pour représenter un rapport (sans dimension, donc sans unité). |
Merci à Jean B.
pour sa contribution
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()