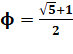NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/12/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Analyse
Débutants Logarithme	LOGARITHME				Glossaire Général
INDEX Analyse	Introduction	Calcul	Exemples	Changement de base
	Log et unités	Propriétés	Décibel	EXPONENTIELLE
	Log Discret	Table	Maths	Historique
		x . ln(x) …	ln(x + 1) < x
		Sommaire de cette page >>> Valeurs typiques >>> Logarithme d'un nombre négatif En construction >>> En gros >>> Principale >>> Valeurs >>> Formules de Ramanujan

LOGARITHMES

PROPRIÉTÉS & VALEURS

Recueil des propriétés et caractéristiques de la fonction logarithme.

Logarithmes naturels de quelques valeurs typiques

Logarithme d'un nombre négatif

Monde réel La fonction logarithme est l'inverse de la fonction exponentielle La base b est positive (non égal à 1). La puissance sera positive. Ce qui impose à x d'être positive Le logarithme d'un réel négatif est indéfini. Note: y peut être négatif. Un exposant négatif correspond au même exposant en positif au dénominateur (5^-2 = 1/5^2 = 1/25)

Monde complexe Dans le monde des nombres complexes, la forme polaire s'écrit: La fonction logarithme complexe devient: Et, elle est définie pour les nombres complexes positifs comme négatifs. Exemple: Autre approche ln(-10) = ln(10 x (-1)) = ln(10) + ln(-1) avec Voir Cette formule ce qui donne: ln(-10) = ln(10) + = 2,303… + 3,141… i

Quelques valeurs de logarithme de nombres complexes négatifs

En construction

EN GROS …		-Ý-
Logarithme naturel ou NÉPÉRIEN (base e)	Logarithme DÉCIMAL (base 10)
Propriétés § Toute fonction logarithme est nulle en 1: elle coupe l'axe des x en x = 1 § L'image réciproque de 1 s'appelle la base du logarithme: la droite y = 1 coupe la courbe pour la valeur de la base § La fonction logarithme est une bijection: un point de x entre 0 et l'infini a une image unique en y de moins l'infini à plus l'infini Logarithme base e en vert et 2, 3, 4, 5, 8, 10 en noir § Notez que l'image des nombres 1 à 10 est ramenée dans une plage plus restreinte de l'axe des y Ø Effet de compression de la dynamique

PRINCIPALES		-Ý-
§ La fonction logarithme est la fonction réciproque de la fonction exponentielle

VALEURS remarquables		-Ý-
log 2 = log 10 2 = 0,30102999…	§ Logarithme décimal de 2 Calcul en remarquant que 2^10 ≈ 1000 et, en prenant la réciproque 10 log 2 ≈ 3
log 2 10 = 3,321928095 log 2 e = 0,3010299957 1/ log 2 10 + 1 / log 2 e = 0,9941771762 ≈ 1	§ Le logarithme d'un nombre en base 2 est presque égal à la somme des logarithmes naturel et décimal de ce nombre (erreur 0,58%) log 2 (x) ≈ ln (x) + log 10 (x)

Formules de Ramanujan
ln (2) = 0,69314 71805 59945 30941 72321 21458 18 …
La convergence est très lente. Pour 1000 itérations, la valeur ne comprend que 7 chiffres significatifs de ln(2).

Voir Ramanujan

ln (3) = 1,09861 22886 68109 69139 52452 36922 5 …
La convergence est également très lente. Pour 1000 itérations, la valeur ne comprend que 7 chiffres significatifs de ln(3).

0,58224 05264 65012 50592 … (En rouge valeur pour k = 100)

0,95023 96051 16643 25903 … (En rouge valeur pour k = 10) Avec Phi le nombre d'or:

Suite	Décibel Logarithmes – Calcul Logarithmes et tout nombre
Voir	Arrondis avec logarithmes Calcul des factorielles avec les logs Croissance Constantes Mathématiques Courbes élémentaires Échelle de Richter Exponentielle Exposants – Index Exposants et puissances Morphisme
DicoNombre	Ln 2 = 0,693… Ln 10 = 2,302 …
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/LogaProp.htm