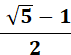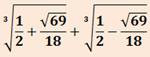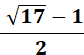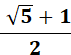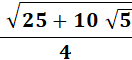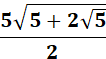|
|||||||||||||||||||||||||||||
![]()
|
NOMBRES IRRATIONNELS Liste de nombres
irrationnels. Sélection des plus typiques parmi une infinité de nombres
irrationnels. SONT IRRATIONNELS tous les nombres qui ne
peuvent pas être exprimés par une fraction de nombres entiers
("non-ration"). Notamment:
|
|
Valeur (25 chiffres) |
Expression |
Nature |
DicoNb |
|
0,693 147 180 559 945 309 417 232 1… |
ln (2) |
Logarithme
naturel de 2 |
|
|
0,433 012 701 892 219 323 381 861 5 … |
|
Aire du triangle équilatéral
de côté unité. |
|
|
0,618 033 988 749 894 848 204 587 0… |
|
Inverse du nombre d'or, aussi son conjugué. |
|
|
0,866 025 403 784 438 646 763 723 0… |
|
Hauteur du triangle équilatéral
de côté unité. |
|
1,059 463 094 359 295 264 561 825 … |
|
Division en demi-tons de la gamme tempérée. |
|
|
1,060 660 171 779 821 286 601 267 … |
|
Taille du cube de Rupert. |
|
|
1,259 921 049 894 873 164 767 211 … |
|
Côté du cube de volume égal à 2, cube unitaire doublé. |
|
|
1,303 577 269 034 296 391 257 099 … |
/ |
Constante de Conway: taux d'expansion de la
suite des commentaires numériques. |
|
|
1,324 717 957 244 746 025 960 908 … |
|
Nombre de
Padovan ou nombre plastique. Racine de F(x) = x3 – x – 1. |
|
|
1,414 213 562 373 095 048 801 689 … |
|
Diagonale du carré unité. |
|
1,561 552 812 808 830 274 910 705 … |
|
Racine
triangulaire de 2. |
|
|
1,618 033 988 749 894 848 204 587 0… |
|
||
|
1,632 526 919 438 152 844 773 496 … |
|
Racine de 2
à la puissance racine de 2. |
|
|
1,720 477 400 588 966 922 759 012 … |
|
Aire
du pentagone unitaire. |
|
|
1,732 050 807 568 877 293 527 446 … |
|
Diagonale
du cube unité. |
|
|
1,839 286 755 214 161 132 551 853 … |
|
Constante de tribonacci. |
|
2,236 067 977 499 789 696 409 174 … |
|
Diagonale du
rectangle 1 x 2. Somme du nombre d'or et de son inverse. |
|
|
2,414 213 562 373 095 048 801 689 … |
|
Nombre
d'argent (un des -). Diamètre du rayon du cercle inscrit de l'Octogone. |
|
|
2,449 489 742 783 178 098 197 284 … |
|
Diagonale du pavé droit 1 x 1 x 2. Diagonale du carré de côté racine de 3. Aire du rectangle racine de 2 x racine de
3. |
|
|
2,598 076 211 353 315 940 291 169 … |
|
Aire de l'hexagone
régulier |
|
|
2,645 751 311 064 590 590 501 616 … |
|
Diagonale du rectangle racine de 2 par
racine de 5. |
|
|
2,718 281 828 459 045 235 360 287 … |
e |
Constante
de Neper égale à exponentielle de 1. |
|
|
3,14 159 265 358 979 323 846 264 … |
|
Constante Pi. Rapport entre le périmètre du
cercle
et son diamètre. |
|
|
3,246 979 603 717 467 061 050 011 … |
Nombre
d'argent (un des -). Une des racines de: x3 – 5x2
+ 6x – 1 = 0 |
|
7,071 067 811 865 475 244 008 445 … |
|
Nombre voisin de 7, connu de Platon |
|
|
7,389 056 098 930 650 227 230 427 … |
|
La constante de Neper (ou d'Euler) est un
nombre irrationnel transcendant. Sa puissance par un nombre rationnel non nul
est un irrationnel. |
|
|
7,694 208 842 938 133 506 425 728 … |
|
Aire du décagone
régulier de côté unité. |
|
|
Irrationalité démontrée par Nesterenko en
1996. |
Voir Table des racines
Transcendants (a fortiori irrationnels)
|
2,665 144 142 690 225 188 650 298 … |
|
Constante
de Gelfond-Schneider. Transcendant. |
![]()
|
Suite |
|
|
Voir |
|
|
Nombres |
|
|
Cette page |
![]()