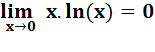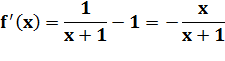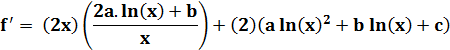|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Limites de polynômes comportant des logarithmes Exemples de problèmes
résolus. Comment s'y prendre? |
|
|
||
|
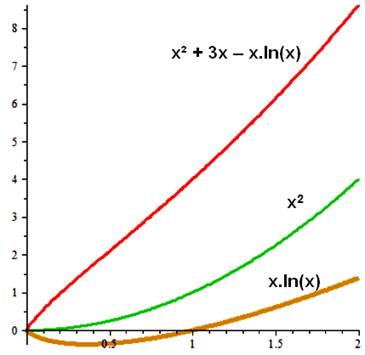
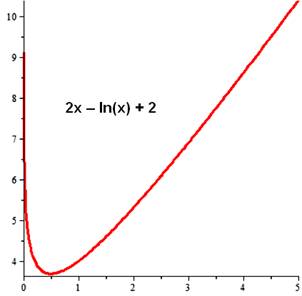
Étudier le comportement de
cette fonction pour x positif; soit dans l'intervalle: Évidemment, nous pouvons
découvrir le graphe à l'aide des outils classiques: calculette ou logiciel mathématique. h(x) est en rouge, visiblement une fonction positive
pour x positif et croissante vers l'infini x² est montré en vert, et x . ln(x) est en ocre;
une contribution négative jusqu'à x = 1 puis positive, mais apparemment
inférieure à la contribution du carré de x. L'enjeu est de démontrer
tout cela. |
|
|
|
Prérequis concernant la fonction logarithme népérien |
|
|
|
Comportement
aux bornes de l'intervalle |
||
|
h(x) |
= x² + 3x – x.ln(x) = x ( x + 3 – ln(x) ) |
|
|
Pour x = 0 |
h(0) = 0 + 3.0 + x. ln(x) (terme qui tend
vers 0) => h(0) tend vers 0 |
|
|
Pour x infini |
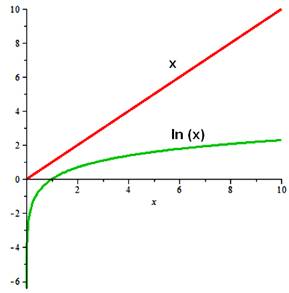
Avec le polynôme factorisé, x tend vers
l'infini; mais que devient le facteur entre parenthèses? On sait que x > ln(x) Voir courbes. Donc le second terme est positif; multiplié
par x qui tend vers l'infini, l'ensemble tend vers l'infini. Pour
x tendant vers l'infini, h(x) tend vers l'infini. |
|
|
|
||
|
On passe par la soustraction
|
f(x) = ln(x + 1) – x |
|
|
Sa dérivée |
|
|
|
Signe pour x > 0, domaine
de définition du logarithme. |
f'(x) > 0 |
|
|
Valeurs aux bornes |
f(0) = ln(1) – 0 = 0 |
|
|
Déduction |
La fonction f(x) est toujours décroissante
à partir de 0. |
|
|
Conclusion pour tout x >
0 |
f(x)
= ln(x + 1) – x < 0 ln(x + 1) < x |
|
|
Et aussi pour tout x > 0 Car ln(x) < ln(x + 1) |
ln(x)
< x |
|
Voir Graphe
|
Dérivée
de h(x) = x² + 3x – x.ln(x) |
||
|
x . ln(x) |
Produit du type u.v dont la dérivées est u'.v + u.v' Ce qui donne:
|
|
|
Et pour h(x),
une simple somme algébrique |
h'(x) = 2x + 3 – ln(x) – 1 h'(x) = 2x
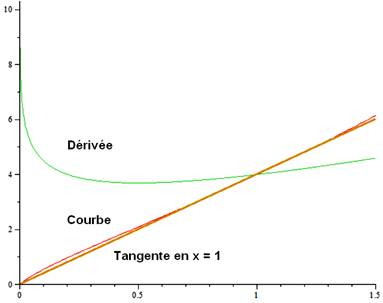
– ln(x) + 2 Le graphe de la
dérivée présente une allure en creux, avec un minimum pour x vers 0,5 et
h'(x) compris entre 3,5 et 3,7. |
|
|
Valeur aux
bornes |
Pour
x = 0: h'(x) = 0 – (–infini) + 2
= infini Pour x
infini: h(x) = infini (car x > ln(x) et a fortiori 2x+ 2 > ln(x) |
|
|
Minimum |
La dérivée y est nulle
(point où la tangente prend la position horizontale). La tangente est donnée par la dérivée (cad: la dérivée seconde) |
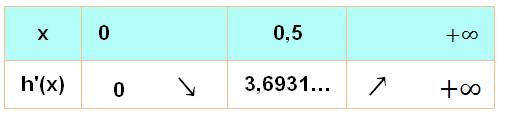
h''(x) = 2 – 1/x + 0 Elle est nulle
pour: 2 – 1/x = 0 x = 1/2 Et la dérivée vaut: h'(1/2) = 1 – ln(1/2) +
2
= 3,6931… |
|
Tableau de
variations |
|
|
|
Analyse
du point d'abscisse x = 1 |
||
|
Point x = 1 |
C'est le point où
le logarithme s'annule h(x) = x² +
3x – x.ln(x) h(1) = 1 + 3
– 0 = 4 |
|
|
Dérivée |
h'(x) = 2x – ln(x) + 2 h'(1) = 2 – 0 + 2 = 4 |
|
|
Tangente |
Sa pente est
égale à la dérivée en ce point. y = 4x + b Elle passe par
ce point (1, 4) 4 = 4 + b b = 0 y = 4x |
|
![]()
|
|
|
|
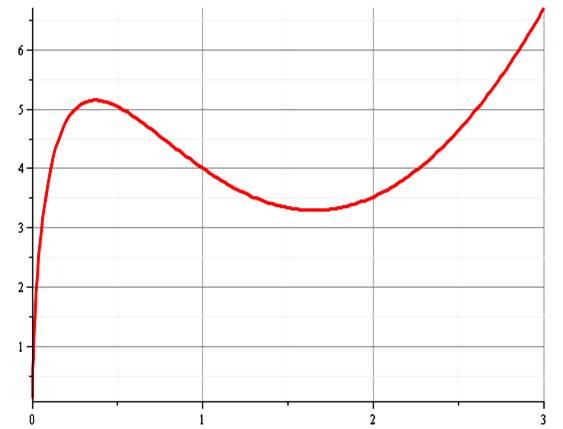
Fonction
comportant un logarithme au carré. Allure du graphe:
Polynôme composé
de deux facteurs. On pose:
|
|
|
Dérivée
de |
|||
|
|
y (fonction) |
y' (dérivée) |
|
|
f = A.B |
f' = AB' +
A'B |
||
|
Facteur
en A |
A = 2x |
A ' = 2 |
|
|
Facteur
en B |
B = B1 + B2 + c |
|
|
|
|
B1 = a . ln (x)² |
|
|
|
|
On peut écrire (ln x)², on préfère ln (x)² en comprenant
bien que ce n'est pas x qui est au carré, sinon on écrirait ln(x²). Ici, il s'agit de la dérivée d'un produit: ln x . ln x Toujours en uv' + u'v. Rappel: la
dérivée de ln x est 1/x. |
||
|
Ce
qui donne |
ln (x)² |
|
|
|
|
a ln (x)² |
|
|
|
Suivant |
B2 = b. ln (x) |
|
|
|
Reprise
de B |
B = a ln (x)² + b ln (x) + c |
|
|
|
Le
produit initial |
f = A.B |
|
|
|
Calcul |
|
f' = |
|
|
Final |
|
f' = |
|
|
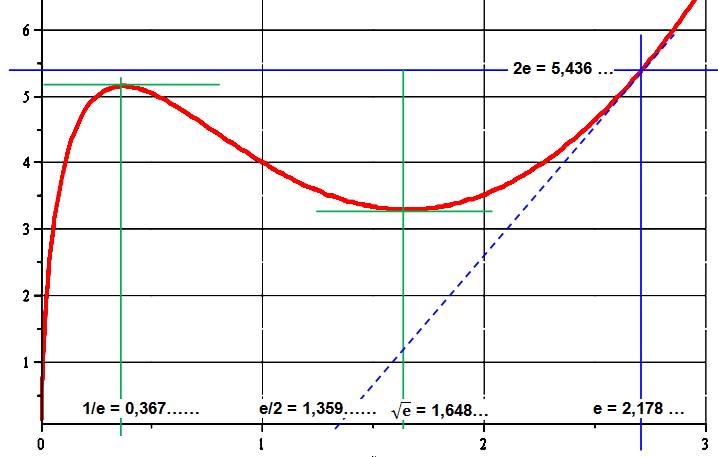
Points de
tangence horizontale |
|
|
La fonction est
paramétrée en a, b et c. Le but est de déterminer ces paramètres en ayant
connaissance de trois points sur la courbe.
On se souvient
que (ou on calcule): ln
(e) = 1 ln (1/e) = – 1 ln ( |
|
|
|
f' = |
|
x= 1/e |
f' =
|
|
x = |
f' =
|
|
x = e |
f' =
|
|
Calcul
des paramètres |
|
|
Nous disposons de
trois équations pour trois paramètres |
|
|
|
|
|
|
|
|
|
|
|
Élimination
des b |
|
|
|
|
|
Différence
|
|
|
Calcul
de b |
|
|
Ce que
deviennent fonction et dérivée |
|
|
Fonction |
|
|
Coordonnées des
points remarquables |
|
|
Dérivée |
f'(x) = f'(x) = f'(x) = f'(x) = |
|
Factorisation |
f'(x) =
|
Voir Exponentielle
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Analyse/Limite/Logarith.htm
|
![]()