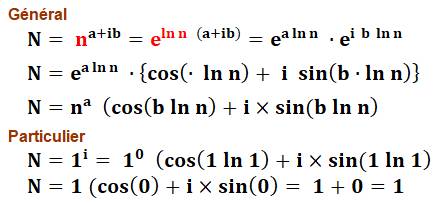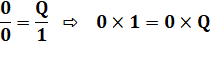|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Culture
|
Le Zéro et l'Infini
est un roman d'Arthur Koestler. Écrit
entre 1938 et 1940, il est publié pour la première fois au Royaume-Uni en
1940, ensuite en France en 1945. Le roman fut originellement écrit en
allemand, sous le titre Sonnenfinsternis, et traduit en anglais sous le titre
Darkness at Noon par une amie de Koestler, Daphne Hardy Henrion. Le texte
original en allemand a longtemps été supposé perdu, mais retrouvé en 2015. |
|
Il est au niveau zéro
de l'intelligence, mais finalement sa position actuelle multiplie son
intelligence par dix. |
|
Dans un sens, je suis quelque chose
d'intermédiaire entre Dieu et le néant. René
Descartes - Le Discours de la Méthode |
|
Qu'est l'homme en regard de la nature ?
Rien par rapport à l'infini, tout par rapport à rien, une moyenne entre rien
et tout. Blaise
Pascal - Pensées |
Voir
Pensées & humour
|
ZÉRO & INFINI en CALCUL Deux faces de la même
pièce: infiniment petit et infiniment grand. 0
ajouté à une
quantité conserve cette quantité.
0
multiplié par une
quantité donne 0
Un nombre
divisé par une quantité qui tend vers 0 donne Un nombre
divisé par une quantité qui tend vers Tout ceci avec quantité non nulle et
non infinie Sinon, se reporter aux tableaux ci-dessous. |
|
|
||||||
|
Tableau récapitulatif
Valeurs données par le
logiciel de calcul Maple
Notez que le
logiciel ne distingue pas le cas de la division de 0 par 0
du cas général de la division de x par 0. Il répond "impossible"
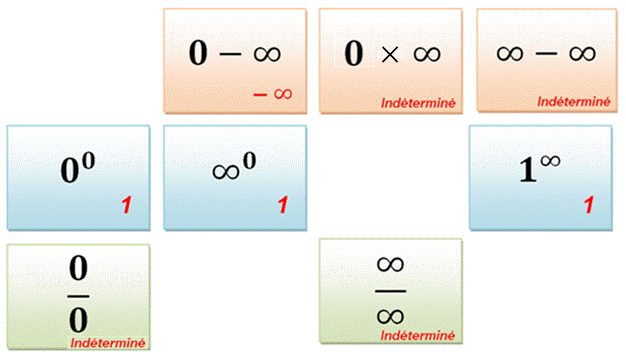
dans tous les cas. Remarque la valeur
de un
puissance infinie est indéterminée, c'est son module en nombre complexe
qui vaut 1. NaN (not a number): En informatique, on obtient NaN pour toutes les opérations qui sont
des indéterminées mathématiques :
|
||||||
Merci à Grégoire Manoélian
pour sa remarque sur la division 0 / 0
Signification des couleurs pour
les tableaux ci-dessous
|
0 + 0 = 0 |
Propriété
classique |
|
i² = –1 |
Définition |
|
|
Résultat
indéterminé |
|
a / 0 = Impossible |
Opération
impossible |
|
|
||||||
|
|
+ |
– |
x |
/ |
Puissance |
|
|
Zéro |
0
+ 0 = 0 |
0
– 0 = 0 |
0
x 0 = 0 |
0
/ 0 = Ind |
0
0 = 1 |
|
|
Infini |
|
|
|
|
|
|
|
Zéro & Infini |
|
|
|
|
|
|
|
Infini & Zéro |
0
+ |
0
– |
0
x |
0
/ |
|
|
|
|
|
|
|
|
|
|
|
Zéro & Un |
0
+ 1 = 1 |
0
– 1 = –1 |
0
x 1 = 0 |
0
/ 1 = 0 |
0
1 = 0 |
|
|
Un & Zéro |
1
+ 0
= 1 |
1
– 0 = 1 |
1
x 0 = 0 |
1
/ 0 = Imp |
1
0 = 1 |
|
|
Un & Infini |
1
+ |
1
– |
1
x |
1
/ |
|
|
|
Infini & Un |
|
|
|
|
|
|
Indéterminé, mais par définition = 1
|
|
||||||
|
|
0 |
1 |
2 |
|
i |
|
|
e |
e 0 = 1 |
e 1 = e |
e 2 = 7,3… |
e ¥ = |
e i = 0,54.. +
i.0,84... |
|
|
i |
i 0 = 1 |
i 1 = i |
i 2 = –1 |
|
i i = |
|
|
|
|
- 1 |
- 2 |
- |
- i |
|
|
e |
|
e -1 = 1/e |
e -2 = 0,13… |
|
e –i = 0,54.. –
i.0,84... |
|
|
i |
|
i -1 = – i |
i -2 = –1 |
|
i –i = 1/ |
|
Voir Nombre complexes
V
|
e |
|
= 2,
718281828… |
|
e |
-1 |
= 0,
3678794412… |
|
e |
2 |
= 7,
389056096… |
|
e |
-2 |
= 0,
1353352833… |
|
e |
i |
= 0,
5403023060… + i . 0, 8414709847… |
|
e |
-i |
= 0,
5403023060… – i
. 0, 8414709847… |
|
i |
i |
= 0,
2078795764… |
|
i |
-i |
= 4,
810477381… |
|
|
|||||
|
|
|
|
|
|
|
|
Infini |
0 |
0 |
|
|
|
|
x
> 1 |
0 |
1 / x n |
x n |
|
|
|
x
= 1 |
Indéterminé / 1 |
1 |
1 |
Indéterminé / 1 |
|
|
0
< x < 1 |
∞ |
1 / x n |
x n |
0 |
|
|
0 |
Impossible |
Impossible |
0 |
0 |
|
|
–1 < x < 0 |
¥ + i . ∞ |
(–1) n / x n |
x n |
0 + i . 0 |
|
|
x
= –1 |
Indéterminé |
(–1) n |
(–1) n |
Indéterminé |
|
|
x
< –1 |
0 |
(–1) n / x n |
x n |
|
|
|
–infini |
0 |
0 |
– |
|
|
|
|
||||||||||
Voir Factorielles |
||||||||||
|
|
|||||||
|
|
0 |
|
1 |
1/Base |
Base |
|
|
|
log a |
Impossible |
– |
log a 1
= 0 |
log a
1/a = – 1 |
log a a
= 1 |
|
|
|
log e |
Impossible |
– |
log e 1 = 0 |
log e 1/e =
– 1 |
log e e = 1 |
log e |
|
|
log e 1/a = – log e a |
log e a + log e
1/a = log e 1 = 0 |
log b a x log a
b = 1 |
|||||
|
exp |
Aucun z n'est solution de: ez = 0 |
||||||
Voir Logarithmes
|
|
|||||||||||||
Voir Puissances |
|||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1i = 1 |
Voir Nombre
à une puissance complexe |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(a + ib)0 = 1 |
Sous sa forme polaire avec alpha = 0 et r non nul:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0(a+ ib) = 0 si partie réelle de z est positive, sinon la valeur n'est pas définie 0i => non défini |
Si w = 0, alors r = 0 et l'angle thêta est quelconque. Alors ln(0)
est indéfini. Si r tend vers 0, alors ln®
tend vers moins l'infini. La limite de wz est nulle si a
est positif |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Si la division donnait le quotient
Q On aurait:
Cette dernière relation est vraie quelle que soit la valeur de Q. Cette division est donc indéterminée. On rappelle que la division est impossible pour toutes les autres
valeurs que 0. Voir le cas de 1infini |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bilan
|
Il
est impossible aux habitants de ce monde de se faire la moindre idée du
néant, de l'infini et de Dieu. Jean d'Ormesson |
![]()
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()