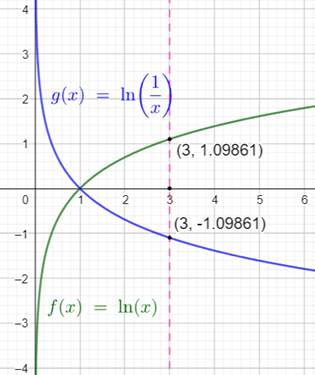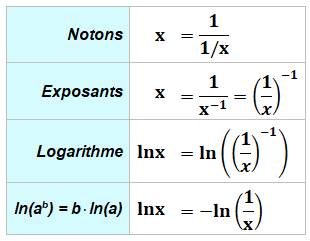|
Édition du: 14/10/2023 |
|
INDEX |
LOGARITHMES |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Pourquoi ln(1/x) = -ln(x) ? Une approche
pour comprendre cette propriété suivie de démonstrations formelles. |
||
|
|
Sommaire de cette page >>> Logarithme de l'inverse d'un nombre >>> Démonstrations |
Débutants Glossaire |
|
Constat Il est curieux de noter que ln (3) et ln (1/3) se
ressemblent. En fait, l'un est l'opposé
de l'autre. Pourquoi ? |
|
|
|
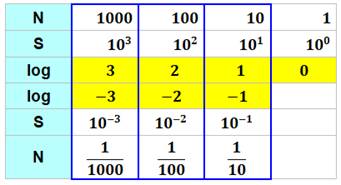
Approche Le tableau montre les valeurs des logarithmes en
base 10 des puissances de 10. En fait, le log indique la quantité de zéros pour
les puissances entières comme fractionnaires. Mais dans le cas fractionnaire, le logarithme est
un nombre négatif. On a donc: log (1000) = 3 et log (1/1000) = -3 |
|
|
|
La fonction logarithme et son
graphe Le graphe présente les deux fonction ln(x) et
ln(1/x), ici en logarithmes népériens (base e et non base 10); nous aurions le
même allure avec les logarithmes à base 10. On retrouve bien les deux mêmes valeurs, l'une
positive et l'autre négative, pour x = 3. Comme le montrent ces graphes: ln(1/x) = - ln(x) |
|
|
|
Formellement Voici la démonstration sans doute la plus simple. Elle se base sur une propriété fondamentale
des logarithmes: la multiplication est remplacée par une addition. On se souvient également que ln (1) = 0. |
|
|||
|
Autre manière de voir On note que x est égal à l'inverse de l'inverse
de x. De cette façon, on introduit un exposant négatif. On sait, par exemple, que |
|
|||
|
Ou encore Cette suite de calculs se comprend en se
souvenant que le logarithme et l'exponentielle sont deux fonctions réciproques. L'une annule
l'effet de l'autre. Ce qui veut dire que: De même que: |
|
|||
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |