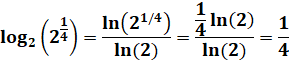|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
LOGARITHMES
- TABLES Quelques
valeurs pour se familiariser. |
|
|
|
|
log 2 = log10 2 = 0, 301 029 ... Calcul Calcul en remarquant que 210 et, en prenant la réciproque 10 log 2
ln 2
= log e 2 = 0, 693
147 … = 1 - 1/2 + 1/3 - 1/4 + ... Exemple 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 +
1/7 - 1/8 + 1/9 - 1/10 + 1/11
- 1/12 + 1/13 - 1/14 + 1/15 - 1/16 + 1/17 - 1/18
= 1632341 / 2450448 = 0,6661398242 Voir Courbe
du nénuphar / Suites typiques /
Nombre
0,393… Cent premières décimales log 2 = 0, 3010299956 6398119521 3738894724
4930267681 8988146210 8541310427 4611271081 8927442450
9486927252 1181861720 ... ln 2 = 0, 6931471805 5994530941 7232121458
1765680755 0013436025 5254120680 0094933936 2196969471
5605863326 9964186875 … Depuis avril 2016, ce nombre est connu avec 500 milliards de décimales (Ron Watkins) Constante de
Mercator ou de Grégory Ln
(1+x) = x - x²/2 + x3/3 - x4/4 + ... Ln (2)
= 1 - 1/2 + 1/3 - 1/4 + ... = série harmonique
alternée Logarithmes
et nombres premiers Hypothèse Soit
N le nombre de décompositions d'un nombre en somme de un ou
plusieurs nombres premiers consécutifs. Exemple 41
= = 11 + 13 + 17 = 2 + 3 + 5 + 7 + 13 => N = 2 Alors La moyenne de N pour tous les nombres jusqu'à l'infini tend vers
0,693 … Record Connu
en 1998 avec 58 486 400 décimales Xavier
Gourdon ; 53 heures de calcul Voir
ln
2 est irrationnel / Transcendant
/ Logarithmes / Théorie des
nombres |
|
|
2,995732274… = ln 2 + ln 10 = ln 4 + ln 5 8,000349495… = ln 42 + ln 71 8,999619342… = ln 81 + ln 100 8,999125391… = ln 88 + ln 92 8,999495877… = ln 89 + ln 91 8,999619340… = ln 90 + ln 90 10,99999763… = ln 102 + ln 587 10,00000743… = ln 198 + ln 822 … |
Voir Presque-entiers
en fractions
|
|
|
|
Principe N (2n) =
n . log 2 Pour
calculer le nombre de chiffres d'une puissance n
de 2, multiplier l'exposant (n) par log
2 et prendre l'entier immédiatement supérieur. Exemple 2127 =>
127 x 0,301 = 38,23 => 39 chiffres |
|
|
|
||
|
Observez la table ci-dessous: La diagonale vaut 1. La ligne 6 est la somme des lignes 2 et 3
(car 2 x 3 = 6). |
log b b = 1 log b 2 + log b
3 = log b 6 |
|
|
Exemples de calcul dans le cas d'une
puissance de la base. |
|
|
Voir Exemple
avec le problème des quatre 4
|
|
b = 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
x = 2 |
1 |
0,6309297534 |
0,5 |
0,4306765582 |
0,3868528073 |
0,3562071871 |
0,3333333333 |
0,3154648769 |
0,3010299957 |
|
3 |
1,584962501 |
1 |
0,7924812507 |
0,6826061949 |
0,6131471930 |
0,5645750342 |
0,5283208337 |
0,5 |
0,4771212549 |
|
4 |
2 |
1,261859507 |
1 |
0,8613531163 |
0,7737056145 |
0,7124143742 |
0,6666666666 |
0,6309297536 |
0,6020599913 |
|
5 |
2,321928094 |
1,464973520 |
1,160964047 |
1 |
0,8982444016 |
0,8270874751 |
0,7739760313 |
0,7324867603 |
0,6989700041 |
|
6 |
2,584962500 |
1,630929753 |
1,292481250 |
1,113282753 |
1 |
0,9207822211 |
0,8616541667 |
0,8154648768 |
0,7781512503 |
|
7 |
2,807354922 |
1,771243749 |
1,403677461 |
1,209061955 |
1,086033133 |
1 |
0,9357849738 |
0,8856218747 |
0,8450980400 |
|
8 |
3 |
1,892789260 |
1,5 |
1,292029675 |
1,160558422 |
1,068621562 |
1 |
0,9463946306 |
0,9030899871 |
|
9 |
3,169925001 |
2 |
1,584962501 |
1,365212389 |
1,226294385 |
1,129150068 |
1,056641667 |
1 |
0,9542425093 |
|
10 |
3,321928095 |
2,095903274 |
1,660964048 |
1,430676558 |
1,285097209 |
1,183294662 |
1,107309365 |
1,047951637 |
1 |
Voir suite en Table
de logarithmes selon diverses bases
|
|
||||||||||
|
|
log 10
10 = 1 log 10 100 = 2 R 2 x
10 = 20 log 2 + log 10 = log 20 0, 3010 + 1
= 1, 3010 |
|||||||||
|
|
n log 10 ln 2 0,3010299957 0,6931471806 3 0,4771212549 1,098612289 4 0,6020599913 1,386294361 5 0,6989700041 1,609437912 6 0,7781512503 1,791759469 7 0,8450980400 1,945910149 8 0,9030899871 2,079441542 9 0,9542425093 2,197224577 10 1 2,302585093 11 1,041392685 2,397895273 12 1,079181246 2,484906650 13 1,113943352 2,564949357 14 1,146128036 2,639057330 15 1,176091259 2,708050201 16 1,204119983 2,772588722 17 1,230448921 2,833213344 18 1,255272505 2,890371758 19 1,278753601 2,944438979 20 1,301029996 2,995732274 21 1,322219295 3,044522438 22 1,342422681 3,091042453 23 1,361727836 3,135494216 24 1,380211242 3,178053830 25 1,397940009 3,218875825 26 1,414973348 3,258096538 27 1,431363764 3,295836866 28 1,447158031 3,332204510 29 1,462397998 3,367295830 30 1,477121255 3,401197382 31 1,491361694 3,433987204 32 1,505149978 3,465735903 33 1,518513940 3,496507561 34 1,531478917 3,526360525 35 1,544068044 3,555348061 36 1,556302501 3,583518938 37 1,568201724 3,610917913 38 1,579783597 3,637586160 39 1,591064607 3,663561646 40 1,602059991 3,688879454 41 1,612783857 3,713572067 42 1,623249290 3,737669618 43 1,633468456 3,761200116 44 1,643452677 3,784189634 45 1,653212514 3,806662490 46 1,662757831 3,828641396 47 1,672097858 3,850147602 48 1,681241237 3,871201011 49 1,690196080 3,891820298 50 1,698970004 3,912023005 51 1,707570176 3,931825633 52 1,716003344 3,951243719 53 1,724275870 3,970291914 54 1,732393760 3,988984047 55 1,740362689 4,007333185 56 1,748188027 4,025351691 57 1,755874856 4,043051268 58 1,763427994 4,060443011 59 1,770852012 4,077537444 60 1,778151250 4,094344562 61 1,785329835 4,110873864 62 1,792391689 4,127134385 63 1,799340549 4,143134726 64 1,806179974 4,158883083 65 1,812913357 4,174387270 66 1,819543936 4,189654742 67 1,826074803 4,204692619 68 1,832508913 4,219507705 69 1,838849091 4,234106505 70 1,845098040 4,248495242 71 1,851258349 4,262679877 72 1,857332496 4,276666119 73 1,863322860 4,290459441 74 1,869231720 4,304065093 75 1,875061264 4,317488114 76 1,880813592 4,330733340 77 1,886490725 4,343805422 78 1,892094603 4,356708827 79 1,897627091 4,369447852 80 1,903089987 4,382026635 81 1,908485019 4,394449155 82 1,913813852 4,406719247 83 1,919078092 4,418840608 84 1,924279286 4,430816799 85 1,929418925 4,442651256 86 1,934498451 4,454347296 87 1,939519253 4,465908119 88 1,944482672 4,477336814 89 1,949390007 4,488636370 90 1,954242509 4,499809670 91 1,959041393 4,510859507 92 1,963787827 4,521788577 93 1,968482948 4,532599493 94 1,973127853 4,543294782 95 1,977723605 4,553876892 96 1,982271233 4,564348191 97 1,986771734 4,574710979 98 1,991226076 4,584967479 99 1,995635195 4,595119850 100 2 4,605170186 |
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()