Ce site est désormais accessible en http://diconombre.fr/index.html et pour cette page voir le lien en fin de page For this page, refer to the link at the bottom.

22 Novembre 2025

NOMBRES - Curiosités, théorie et usages

Accueil DicoNombre Rubriques Nouveautés Édition du: 08/04/2026

Orientation générale  DicoMot Math Atlas Références M'écrire

Barre de recherche DicoCulture Index alphabétique

CONJECTURES

Débutants

Multiplication

MORDELL-FALTINGS

Glossaire

Facteurs et Diviseurs

INDEX

Facteurs et diviseurs

Conjectures

Théorème

Sommaire de cette page

>>> Mordell et Faltings

>>> Théorème

>>> Conséquences

Théorème de Mordell–Faltings

Quantité finie de solutions pour certaines équations diophantiennes. Conjecture émise par Mordell en 1922 et prouvée par Faltings en 1984.

Mordell et Falting

Louis MORDELL (1888-1972), américain naturalisé britannique, spécialiste de la théorie des nombres. Il étudie en particulier l'équation y² = x³ + k et la résout pour de nombreuses valeurs de k. Puis, il s'attaque aux équations indéterminées des troisième et quatrième degrés. Il prouve en 1917 la conjecture de Ramanujan sur la fonction tau, en appliquant sa connaissance des fonctions modulaires à la théorie des nombres. De même pour la conjecture de Poincaré sur la génération du groupe des points rationnels d'une courbe elliptique. Il émet sa célèbre conjecture. En 1945, Mordell succède à Godfrey Hardy (1877-1947) à la chaire Sadleirian de l'université de Cambridge.

Gerd FALTINGS (1954-), allemand. Il prouve la conjecture de Mordell et obtient la médaille Fields (1986) pour ce résultat.

Théorème de Mordell-Faltings

Ce qu'il dit: Une courbe algébrique, de genre au moins égal à 2, ne peut admettre qu'un nombre fini de points à coordonnées rationnelles. Les surfaces engendrées par une équation diophantienne, et présentant un deux trous ou plus, possède une quantité finie de solutions en entiers gaussiens n'ayant aucun facteur commun. Explications Ce théorème de la théorie des nombres indique que certains systèmes d'équations algébriques à coefficients rationnels n'ont qu'un nombre fini de solutions rationnelles. Si, le genre d'une courbe algébrique plane de degré n est l'entier (n – 1) (n – 2 ) / 2 diminué des ordres de multiplicité des points singuliers de la courbe dans le plan projectif complexe. Le genre d'une courbe est le nombre de fois où il est possible de couper cette courbe sans obtenir 2 morceaux distincts. Alors, une courbe algébrique, de genre au moins égal à 2, ne peut admettre qu'un nombre fini de points à coordonnées rationnelles. Sa démonstration est acquise depuis 1984. Mais avec la démonstration de la conjecture ABC, celle-ci serait grandement simplifiée. Elle donnerait également un moyen de déterminer les points rationnels.

Conséquences du théorème

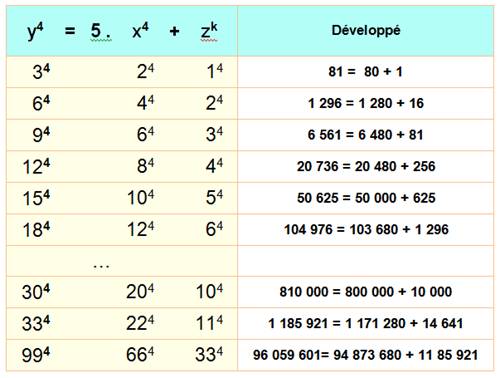
Théorème de Fermat-Wiles L'équation de Fermat-Wiles (x^n + y^n = z^n) est diophantienne et présente (n – 1) (n – 2) / 2 tous. Ce qui implique, selon ce théorème, que pour tout entier supérieur à 3, la quantité de solution est finie. On sait depuis 1994 que cette quantité est même nulle. Équation de degré 4 L'équation x^4 = 5y^4 + z^k n'a, pour chaque valeur de k > 3, qu'un nombre fini de solutions dont les termes sont premiers entre eux. Exemples (ici, par forcément avec des premier entre eux) Toutes ces égalités sont issues de la même racine (première ligne) par multiplication.

.

Suite	Conjecture ABC Conjectures Sept problèmes du millénaire
Voir	Facteurs et diviseurs
Cette page	http://diconombre.fr/aMaths/Factorisation/Mordell.htm