NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/10/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puissances
Débutants Logarithmes	Triplets de Pythagore					Glossaire Puissances
Rubrique PARTITION INDEX PUISSANCES	Introduction	Propriétés		Cercle	Historique
	Primitif	Génération		Matrice	Spéciaux
	Illustration	Triangles		Briques	Calculs
	Avec un carré
			Sommaire de cette page >>> Triangles rectangles particuliers >>> Triangles de même hypoténuse >>> Périmètre >>> Surfaces >>> Théorèmes de Fermat – Démonstration >>> Cercles >>> Curiosités >>> Triangle entier >>> Historique

TRIANGLES de PYTHAGORE

Triangles rectangles dont les longueurs des côtés sont des nombres entiers.

Fermat a démontré que pour de tels triangles, l'aire n'est jamais un nombre carré >>>.

TRIANGLES PARTICULIERS

Les 2 plus petits à côtés entiers de même hypoténuse.	Côtés	1, 8	4, 7
	Hypoténuse	65	√65

Les 2 plus petits à côtés entiers de même hypoténuse entière	Côtés	7, 24	15, 20
	Hypoténuse	25	25

Les 2 seuls ayant cette propriété: même aire et même périmètre	Triangle	6, 8, 10	5, 12, 13
	Surface	24	30
	Périmètre	24	30

Le plus petit triangle ayant cette propriété.	Triangle	119, 120, 169
	Hypoténuse	169 =	13²
	Côtés	120 – 119 =	1²

Le plus petit triangle ayant cette propriété. Fermat 1643	Triangle	A = 4 565 486 027 761 B = 1 061 652 293 520 C = 4 687 298 610 289
	Hypoténuse	C = 2 165 017²
	Côtés	A + B = 2 372 159²

C'est bêbête.	Triangle	693, 1924, 2 045
	Aire	666 666

Seuls trio de triangles connus ayant la même aire.	Triangle	1 380 19 019 19 069	3 059 8 580 9 109	4 485 5 852 7 373
	Aire	13 123 110

Trouvé en 1945 par Shedd d'Arlington, cité par Martin Gardner

On n'en connaît d'autres de même aire.

On ne sait même pas s'il en existe d'autres.

Le trio le plus petit ayant le même périmètre.	Triangle	3 255 5 032 5 993	7 055 168 7 057	119 7 080 7 081
	Périmètre	14 280

Triangles rectangles de même hypoténuse
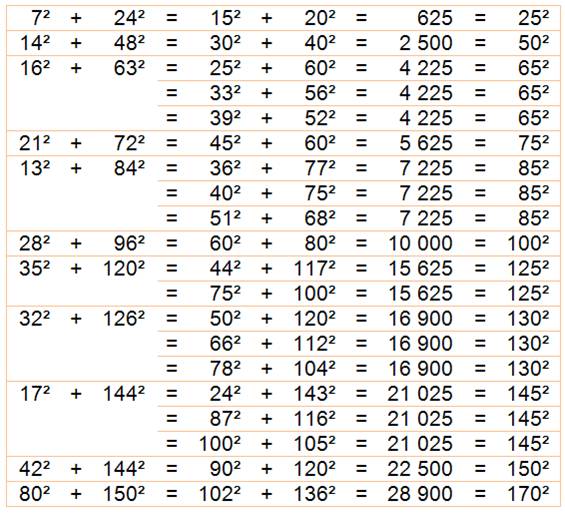
Les dix plus petits avec hypoténuse non entière Avec hypoténuse entière Pour tous a, b, c, d < 151.

Voir Somme de plusieurs carrés

PÉRIMÈTRE
Le périmètre du triangle est: a + b + c. Dans le cas où le triplet est (u² - v², 2uv, u² + v²), le périmètre est: 2u (u + v).

SURFACE - AIRE

Aire d'un triangle pythagorique L'aire d'un triangle pythagorique est toujours un multiple de 6. Fibonacci (1175-1240) Aire carrée – Théorème de Fermat sur les triangles rectangles Aucun triangle pythagorique n'a une aire carrée. Autrement dit: le système d'équations diophantiennes suivant n'a pas de solution: Voir Démonstration Conséquences Si trois nombres carrés sont en progression arithmétique, la raison d'une telle suite ne peut pas être, elle aussi, un nombre carré. Il est impossible de trouver deux triangles rectangles tels que présentés sur cette figure.

Voir Brève 729

L'aire d'un triangle est évidemment ab / 2.

Dans le cas où le triplet est (u² – v², 2uv, u² + v²), l'aire est uv (u² – v²).

En moyenne, l'aire se termine par 0 pour 2/3 des cas.

En fait,

Trois cas possibles seulement:

Unité de l'aire	0	4	6
Pourcentage des cas en moyenne	66%	33%	33%

L'aire d'un triangle dont les côtés sont des nombres rationnels:

ne peut pas être 1, 2, 3 ni 4;

Le premier entier a posséder cette propriété est 5;

Le premier avec des côtés en nombres entiers est 6.

	a	b	c	A = a.b / 2
Rationnel	3/2	20/3	41/6	5
Entier	3	4	5	6

Suite en Nombres congruents

Théorème de Fermat sur les triangles rectangles
Aucun triangle pythagorique n'a une aire carrée.	Autrement dit: le système d'équations diophantiennes suivant n'a pas de solution:
Démonstration d'après Fermat – Descente infinie Voir Divisibilité par 4 de la somme ou la différence de deux nombre impairs

Merci à Jean-Francisque Léo pour ses remarques

La démonstration de Fermat

Number Theory: An approach through history

From Hammurapi to Legendre – Page 76 - André Weil

CERCLES
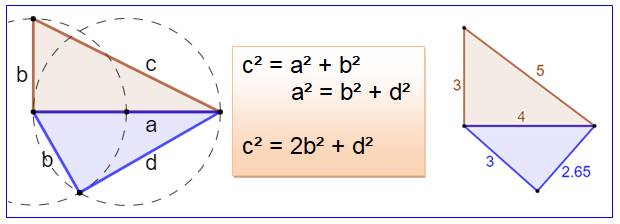
Cercle	Inscrit	Circonscrit
Diamètre	(x + y) - z = 2 v (u - v)	hypoténuse = diamètre
Exemple 3, 4, 5	2	5
Nombre entier	Rayon entier	Diamètre entier

CURIOSITÉS
Les triangles suivants sont rectangles: 3, 4 , 5 : 3² + 4² = 5² 5, 12, 13 : 5² + 12² = 13² En prenant les moyennes, est-ce que le triangle reste rectangle? 4, 8, 9 : 4² + 8² = 80 au lieu de 9² = 81. L'angle n'est pas droit, mais vaut 91 degrés.

Triangle entier
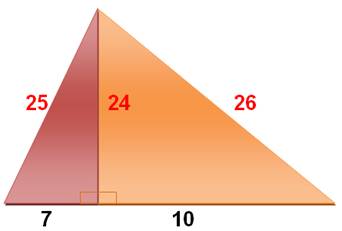
Problème Dans ce triangle, toutes les mesures sont entières; de plus, h, b et c sont consécutifs. Quel est le plus petit triangle de cette sorte? Solution On montre que: y² = 2 (x² + 1). Ce qui veut dire que: y² est divisible par 2; => y est divisible par 2; => y² est en fait divisible par 4; => (x² + 1) est divisible par 2; => y est impair et x est pair. Explorons! Réponse x = 7 et y = 10 pour le plus petit; mais il y en a d'autres plus grands. Le premier cas avec h = 0 correspond à un triangle dégénéré en angle plat.	Relations h = b – 1 => h² = b² – 2b + 1 c = b + 1 => c² = b² + 2b + 1 x² = b² – h² = b² – b² + 2b – 1 = 2b – 1 y² = c² + h² = b² + 2b + 1 – b² + 2b – 1 = 4b y² – 2x² = 4b – 4b + 2 = 2 y² = 2 (x² + 1)

Vu dans Tangente de septembre-octobre 2013 – Michel Criton

Voir Le triangle 13, 14, 15 du même genre

Historique

1225 – Fibonacci: publie une liste de problèmes dont l'un est de trouver trois carrés en progression arithmétique. Il nomme la raison congruum. Il propose l'exemple indiqué pour un congruum de 5.

La même année, il publie Liber Quadratorum et remarque que le conguum ne peut pas être un nombre carré.

Bachet de Méziriac (1581-1638), traduisant le livre Arithmetica de Diophante, s'intéresse aux triangles rectangles de Pythagore et affirme qu'aucun d'eux n'a une aire carrée. Autrement dit: x² = y² + z² et y.z = 2t² n'a pas de solution.

Fermat (vers 1601-1665) s'empare de ce sujet en lisant les Arithmétiques de Diophante, traduites et commentées par Bachet. Il défie ses contemporains de prouver que les triangles de Pythagore ne présentent jamais une aire carrée.
Fermat écrit à Huygens: si l'aire d'un tel triangle était un carré, alors, il en existerait un plus petit ayant les mêmes propriétés et ainsi de suite. Ce qui est impossible. Principe de sa démonstration par descente infinie. Heureusement in annotera sa démonstration sur le livre de Diophante.
En 1670, après sa mort, son fils Samuel découvre la démonstration et la publie.

En 1676, deux ans après sa mort, on publie Traité des triangles rectangles en nombres de Frénicle de Bessy. On y trouve une démonstration qui certainement est celle de Fermat, attestée par les échanges entre les deux mathématiciens et Huygens.

En 1738, Euler présente une preuve plus simple en partant d'un énoncé équivalent: v⁴ + t⁴ = s², équation qui n'a pas de solution entière non triviale.

Histoire détaillé en: Number Theory: An approach through history

From Hammurapi to Legendre – Page 76 - André Weil

Suite	Briques de Pythagore Nombres congruents
Voir	Addition - Glossaire Années Pythagore Décade de Pythagore Nombres sommes de carrés plusieurs fois Programmation Pythagore – Biographie
Sites	Théorème de Fermat sur les triangles rectangles – Wikipédia Fermat's Right Triangle Theorem – Wikipedia Fermat's Right Triangle Theorem – Proof Wiki Pythagorean Triple de Eric Weisstein
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/TripTrg.htm