|
||||||||||||||||||||||||||||||||||||||||
![]()
|
CONJECTURE DE POINCARÉ Émise par Henri Poincaré en (1904) Prouvée par Grigori Perelman (2002-03)
Un célèbre problème de la topologie vient d'être
démontré après des dizaines d'années d'effort de la part de nombreux
mathématiciens. En bref La sphère (topologique*) est le seul espace tridimensionnel fermé dépourvu de trous. |
*Équivalence topologique
|
Dans le monde de la topologie, le monde
des objets élastiques, déformables continûment, le pavé, le cube ou la sphère
font partie de la même catégorie d'objets sans trou. On dit qu'ils sont
homéomorphiques. Avec un trou, on trouve le tore, le doughnut ou encore la
tasse de café avec une anse. En savoir plus >>> Anglais: The
cube and the sphere are homeomorphic, as are the coffee cup and the doughnut.
But the circle is not homeomorphic to the doughnut. |
|
|
||
|
Évident?
Sphère et tore
Voir Objets
topologiques Surface fermée sans
trou
Caractérisation –
Invariant
|
Explications
Elles sont appelés "variétés"
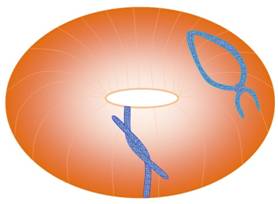
Sur cette
coquille, le lasso peut se refermer complètement.
Sur ce tore,
un des lassos ne peut passe refermer complètement. |
|
Voir Groupe fondamental / Géométrie / Sphère / Sphère-calcul
|
Autre façon de voir |
|
|
|
Ballon
|
Bouée
|
|
|
|
||
|
Surface 2D en espace 3D
Surface 3D en espace 4D
|
Propriété unique La sphère est le seul espace bidimensionnel fermé dépourvu
de trous. Conjecture de Poincaré La boule est le seul espace tridimensionnel fermé
dépourvu de trous. En
langage commun: Tout
corps qui ne contient pas de trous et qui n'est pas tordu peut être
transformé en sphère. Autre Toutes
les variétés compactes contractiles peuvent être déformées en une sphère. Telle
que l'a écrite Poincaré: Tout
polyèdre dont les nombres de Betti sont égaux
à un et qui est dépourvu de torsion est simplement connexe. Formulation
moderne: Une variété de dimension 3 qui a le même groupe d'homologie que la sphère de dimension 3 lui est homéomorphe. |
|
|
|
|
|
Principe de la méthode Poincaré
Plus formellement
Est-ce
vrai pour la "sphère" (nD) de l'espace (n+1)D? Traduite en langage maths: Définition: un
surface dans l'espace à n dimensions est une variété; Question: Est-ce
qu'une variété compacte de l'espace à n + 1 dimensions est homéomorphe à la
sphère n-dimensionnelle? |
|
|
HISTORIQUE de la conjecture de Poincaré selon
la dimension |
|
||
|
n |
Objet |
Qui, quand |
|
|
1 |
|
Trivial. |
|
|
2 |
|
Connu
depuis le XIXe |
|
|
3 |
|
Conjecture
de géométrisation. Prouvée
par Grigori Perelman en 2003. |
|
|
4 |
|
Prouvé
par Freedman en 1982. Médaille
Fields pour ce travail en 1986. |
|
|
> 4 |
|
En
1960 et 1961 indépendamment par: Stephen Smale, John Stallings, Andrew
Walace, et Zeeman
|
|
|
Mathématicien
russe très discret.
Médaille
Fields en 2006. Prix qu'il a
refusé, comme tous les autres. |
|
|
|
|
Géométrisation Au-delà
de la vision topologique, les surfaces de dimensions 3 ont été dotées
récemment de moyens de mesurer les distances entre les points (Thurston -
années 70). |
|
Voir Outils
topologiques ayant servie à la démonstration
|
|
|
|
|
|
|
|
|
|
|
|
![]()
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Revue |
|
|
Livre |
|
|
Cette page |
![]()