NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/09/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Théorie des Nombres
Débutants Général	Le petit théorème de Fermat			Glossaire Général
INDEX Théorie des nombres	Découverte	Exploration	Démonstration	Généralisation
	Perles et collier	Applications	Puissances	Avec Pascal
		Sommaire de cette page >>> Triangle de Pascal >>> Petit théorème de Fermat >>> Développement de la puissance d'une somme

PETIT THÉORÈME DE FERMAT

en pratique

Une règle très utile, basée sur une propriété exceptionnelle du triangle de Pascal et le développement des puissances. Occasion de démontrer le petit théorème de Fermat.

TRIANGLE DE PASCAL et une de ses propriétés étranges

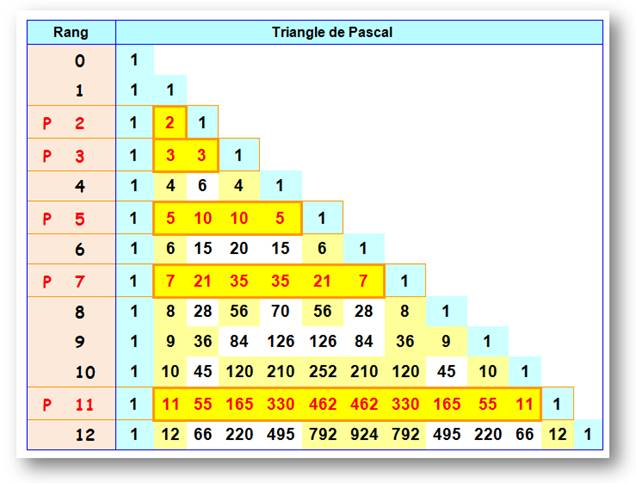
On cherche une propriété particulière des coefficients du triangle de Pascal. Éliminons les bords de chaque côté (les "1" en bleu); on s'intéresse au centre. On note en jaune, les cellules divisibles par la valeur de la ligne à laquelle elles appartiennent. Encadrons, les lignes dont la valeur est un nombre premier. Observations Seules les lignes encadrées sont complètement jaunes et elles seules. Autrement-dit: sur ces lignes des nombres premiers toutes les valeurs de la ligne sont divisibles par le nombre, sauf les extrémités (valeur 1). Tous les nombres du triangle de Pascal situés sur une ligne de rang premier sont divisibles par le rang (sauf extrémités).

Développement de la puissance d'une somme

Le développement de la puissance d'une somme de deux termes fait appel au triangle de Pascal. Les coefficients (dits coefficients du binôme de Newton) sont ceux du tableau ci-dessus.

(a + b)^2 =	a^2 + 2ab + b^2
(a + b)^3 =	a^3 + 3a^2 b + 3a b^2 + b^3
(a + b)^4 =	a^4 + 4a^3 b + 6 a^2b^2 + 4a b^3 + b^4
(a + b)^5 =	a^5 + 5a^4 b + 10 a^3b^2 + …
(a + b)^n =	Motif semblable avec pour coefficients les valeurs sur la ligne n du triangle de Pascal.

Or, tous ces coefficients, sauf ceux des extrémités (ceux qui s'appliquent à aⁿ et à bⁿ), sont divisibles par n, lorsque n est premier.

Si p est premier, tous les coefficients, sauf le premier et le dernier, du développement de (a + b) ^p sont divisibles par p.

(a + b) ^p = a^p + b^p + k.p

Généralisation: la formule générale suivante existe aussi:

(a + b + c + d +...)^p = a^p + b^p + c^p + d^p + ... + k.p

Petit théorème de Fermat

Avec ces notions nous voici prêts pour aborder le petit théorème de Fermat Cas où tous les termes sont égaux à 1 Alors a + b + c + d +... = 1 + 1 + 1 + … = N et, selon la loi trouvée ci-dessus N^p = N + k.p Ex: 3^5 = 3 + 5p; en effet 3^5 = 243 = 3 + 5 x 48 Un nombre porté à une puissance première p diminué de lui-même est un multiple de p. N^p = N + k.p N^p – N = k.p N (N^p – 1 – 1) = k.p Cas où N et p sont premiers entre eux Le nombre p ne divisant pas N, il divise l'autre facteur dans la dernière expression ci-dessus. N^p – 1 – 1 = k.p  C'est le petit théorème de Fermat.

Suite	Démonstration du petit théorème de Fermat Conséquences sur les nombres premiers Application aux opérations sur les puissances
Voir	Identités remarquables Coefficients du binôme Petit théorème de Fermat
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/DivisiFe.htm