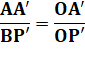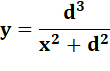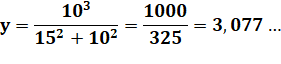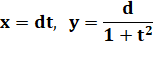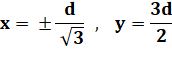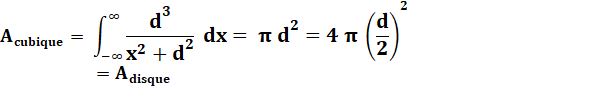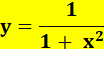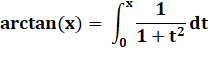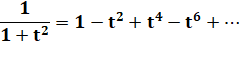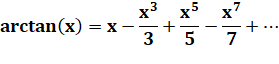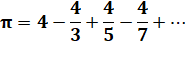NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/03/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	COURBES			Glossaire Géométrie
INDEX Courbes Géométrie	Droite	Élémentaires	Spirale	Cubique d'Agnesi
	Arabesque	Autres (cœur)
	** signale des notions avancées	Sommaire de cette page >>> Construction >>> Équation >>> Graphe >>> Propriétés >>> Formule pour Pi		Maria Gaetana Agnesi

Cubique d'Agnesi

Agnésienne, Sorcière d'Agnesi ou Cloche de Cauchy

Courbe construite à partir d'un cercle et une tangente.

Étudiée par Fermat (1630), Guido Grandi (1703) puis Maria Agnesi (1748) dans son livre Istituzioni analitiche.

Gregory, Newton ou Leibniz étudieront aussi cette courbe pour d = 1.

Anglais: witch of Agnesi / Versiera

Petite histoire de sorcière

Le géomètre Guido Grandi (1671-1742) nomme cette courbe: versiera, d'après un terme de marine qui était une corde qui servait à virer de bord. Un certain Colson commet une méprise en traduisant en anglais avversieara qui signifie adversaire, ou surnom de sorcière, au lieu de versiera. Depuis, la courbe est connue comme: la sorcière d'Agnesi. Alors qu'Agnesi était … religieuse!

Source: Les femmes et les mathématiques – Joachin Navarro – Le monde est mathématique

Construction de la cubique d'Agnesi
Un cercle de centre C et de diamètre OT = d. Un point quelconque A sur le cercle. La droite OA coupe une tangente en B. Le point P (x, y) est tel que x = abscisse de B et y = ordonnée de A. Autrement dit: BP perpendiculaire à TB et AP parallèle à TB. La cubique d'Agnesi est le lieu des point P lorsque A se déplace sur le cercle.

Équation de la cubique
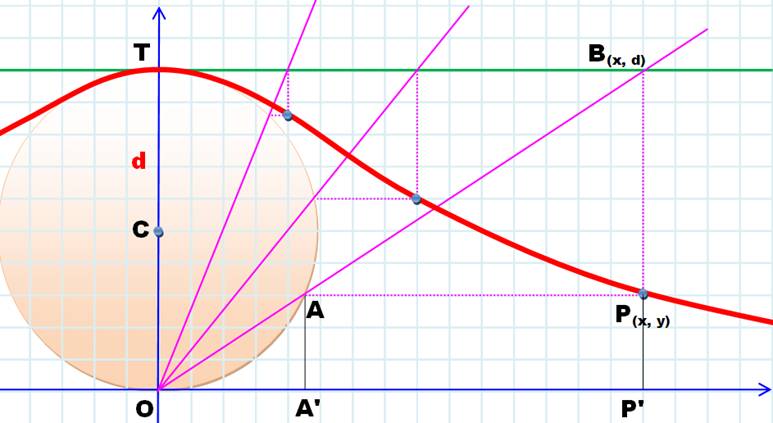
Les triangles OAA' et OBP' sont semblables. Application du théorème de Thalès.
Avec les coordonnées correspondantes et en faisant les produits.	y . x = xA . d
Élévation au carré (distances symétriques par rapport à Oy).	y² . x² = xA². d²
Équation du cercle de centre C(0, d/2):	(x – 0)² + (y – d/2)² = (d/2)² x² + y² – yd + d²/4 = d²/4 xA² = yA (d – yA)
Avec les coordonnées du point A sur le cercle et avec yA = yP = y	y² . x² = y (d – y) . d²
Sachant que y est toujours positif (donc non nul).	y . x² = (d – y) . d² y . x² = d^3 – y d² y (x² + d²) = d^3
Présentation classique:
Vérification pour P(15, y?).
Équation paramétrique:
Équation polaire paramétrique:

Graphe de la cubique avec d = 10 (selon la figure)

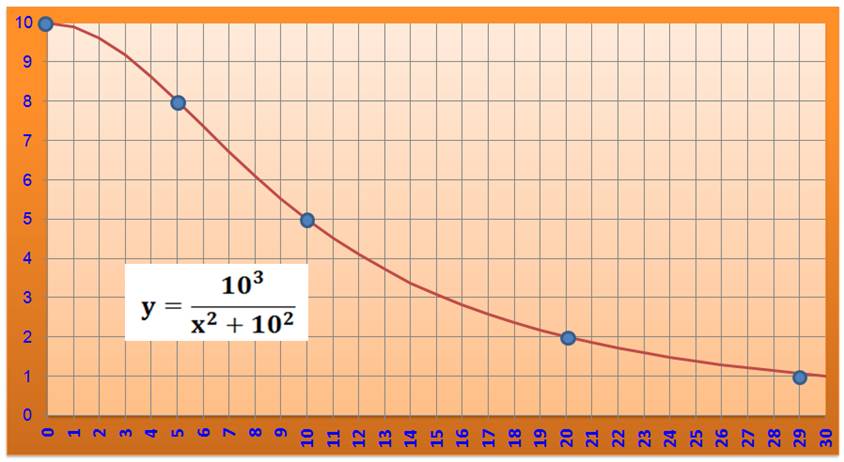
Disques bleus: valeurs entière de y pour x entier.

Propriétés

L'axe des x (droite y = 0) est une asymptote. L'axe des y (droite x= 0) est un axe de symétrie (même valeur de y pour des valeurs opposées de x). Le cercle de centre C est appelé le cercle surosculateur en T de la cubique d'Agnesi. Point d'inflexion pour: L'aire entre la courbe et son asymptote (l'axe des x) vaut quatre fois l'aire du disque: Le volume engendré par la cubique tournant autour de l'axe des abscisses vaut Le centre de gravité se situe au point G (0, d/4). Forme simplifiée avec d = 1

Formule de Leibniz pour Pi**
Expression de l'arc tangente
Or
En intégrant
Pour Pi = 4 arctan(1)

Suite	Voir en-tête Maria Agnesi (1715-1799)
Voir	Courbure Dirac (1902-1984) Gauss (1777-1855) Géométrie – Index Hyperbole Topologie
Sites	Cubique d'Agnesi – Mathcurve Sorcière d'Agnesi – Wikipédia Maria Gaetana Agnesi et la sorcière – Alessandra Sarti – Vie et œuvre d'Agnesi (daiporama pdf – 26 pages) Witch of Agnesi – Wolfram MathWorld – Voir l'animation.
Cette page	http://villemin.gerard.free.fr/Geometri/Courbes/Agnesi.htm