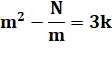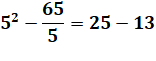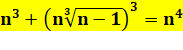NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/03/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ADDITION
Débutants Addition	PARTITION				Glossaire Addition
Rubrique PARTITION Cubes Racines et puissances	Entiers & Carrés	Cubes		Puissances 4...n
	Somme de 4 carrés Théorème de Lagrange		Somme de n puissances Théorème de Waring
	1 à 100 en 4 carrés		Problèmes des trois cubes
	Sommes de carrés, cubes et autres puissances
	Comprendre les sommes de carrés
	Sommaire de cette page >>> Partition et cubes – Les problèmes que l'on se pose – Index >>> Somme de n cubes >>> N = Somme de deux cubes >>> N = Somme de trois cubes >>> Somme de n cubes, plusieurs fois >>> Cube, somme de n cubes >>> Carré, somme de n cubes >>> Cubes de nombres consécutifs >>> Curiosités >>> Liste des sommes des puissances des cubes de nombres consécutifs >>> Somme de cubes bien en forme!

PARTITION des NOMBRES

en SOMME de CUBES

Cas des nombres Taxicab

Somme de cubes, une fois ou plusieurs fois

Puissance somme de cubes

Curiosités

Généralisation à toute puissance, voir: Théorème de Waring

Voir Table des puissances des nombres

Partition et cubes – Les problèmes que l'on se pose
1	Somme de nombres consécutifs au cube
11	Entier, pairs, inverses …	1^3 + 2^3 + 3^3 + … + n^3	>>>
12	Plage de nombres consécutifs	3^3 + 4^3 + 5^3 + … + n^3	>>>
13	Somme des cubes = somme des entiers au carré	1^3+ 2^3 + 3^3 = (1 + 2 + 3)^2	>>>
2	Partition des nombres en cubes / Nombre = sommes de cubes
21	k cubes (jusqu'à k = 9)	N = x^3 + y^3 + …+ u^3 (Waring)	>>> >>>
22	k cubes distincts		>>>
23	Nombres positifs ou négatifs au cube	Cas de 33 (récalcitrant)	>>>
24	Somme de cubes = cube	x^3 + y^3 = z^3 (Fermat) x^3 + y^3 + z^3 = t^3	>>> >>>
25	Somme de cubes = puissances	x^3 + y^3 +…+ z^3 = t^k	>>>
26	Somme de cubes k fois (comme les Taxicab)	1729 = 1^3 + 12^3 = 9^3 + 10^3	>>>

Voir Partition – Index / Somme de puissances / Tables sur les cubes

Merci à Jean D.

SOMME de n CUBES

9 cubes

Tout entier est décomposable

en somme d'au plus

neuf cubes.

2 nombres seulement

nécessitent 9 cubes.

Voir Théorème de Waring

Les deux seuls qui nécessitent les 9 termes.

23 =	2. 2^3 + 7. 1^3
239 =	2. 4^3 + 4. 3^3 + 3. 1^3

Si on admet les cubes négatifs

23 =	3^3 + 4 . (-1)^3 soit 5 termes

8 cubes

15 nombres seulement

nécessitent 8 cubes.

15, 22, 50,

114, 167, 175, 186,

212, 213, 238,

303, 364,

420, 428, et 454

7 cubes

Tout entier suffisamment grand

est décomposable en somme

d'au plus sept cubes.

8042 est probablement le plus grand entier qui ne peut pas être décomposé en moins de 7 cubes.

5 cubes

Tout nombre est décomposable

d'une infinité de manière en somme

de 5 cubes positifs ou négatifs.

4 cubes

Tout entier qui ne laisse pas un reste de 4 ou 5 lors d'une division par 9, peut se décomposer en somme de 4 cubes positifs ou négatifs.

3 cubes

Tout nombre de la forme 9k 4 n'est pas somme de trois cubes, car:

15 nombres inférieurs à 100 sont somme de trois cubes.

Le nombre 33 est le plus petit nombre dont on ne connait aucune somme de trois nombres (positifs o négatifs) au cube. Voir Suite

2 cubes

Tout nombre de la forme 9k 3 ou 9k 4 n'est pas somme de deux cubes.

Voir conditions >>>

9 nombres inférieurs à 100 sont somme de deux cubes.

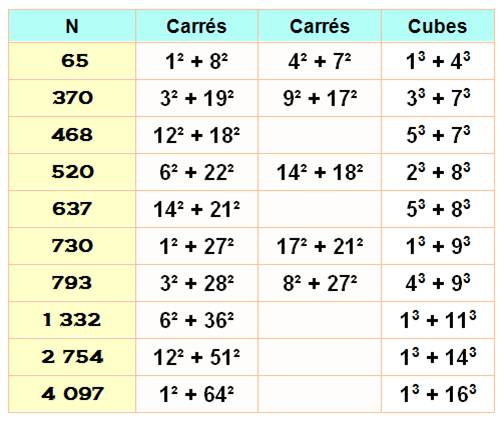
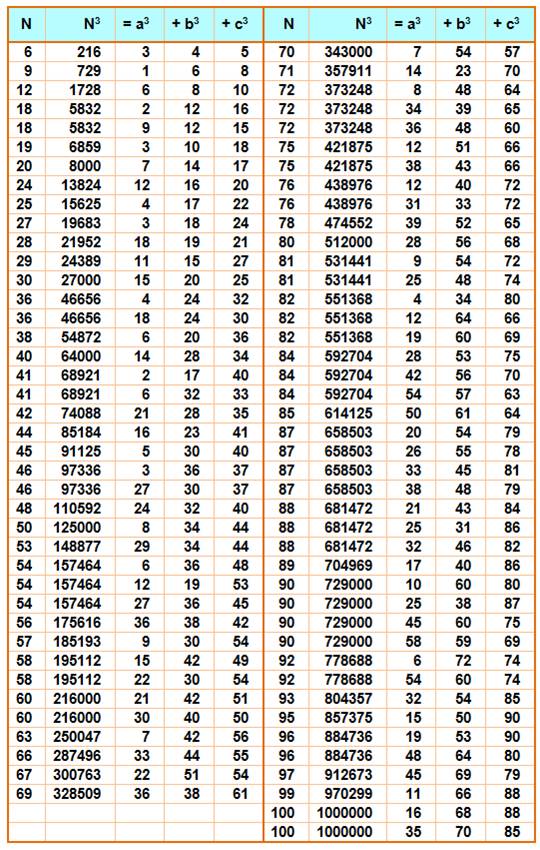
Liste des sommes de k cubes jusqu'à n = 100

En rouge: nombres successifs, sauf si une somme à été réalisées avec moins de termes (nombres en noir au-dessus)

En couleur ocre en bas, les sommes déjà atteintes avec moins de termes.

Ex: 26 est atteint par la somme de 5 cubes, pas moins. Pour 27, un seul suffit et il en faut deux pour 28.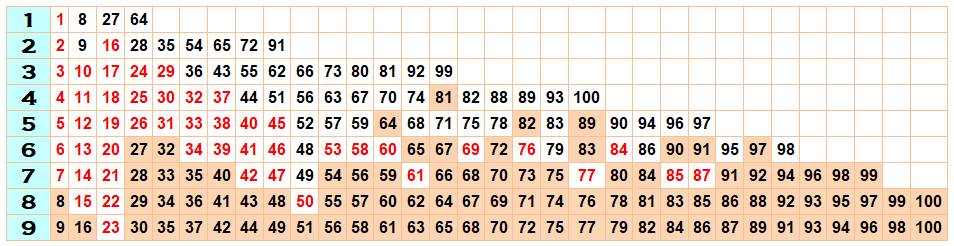

Voir Tables de partitions en cubes / Tables de sommes de cubes /

Conditions pour que x^3 + y^3 = N
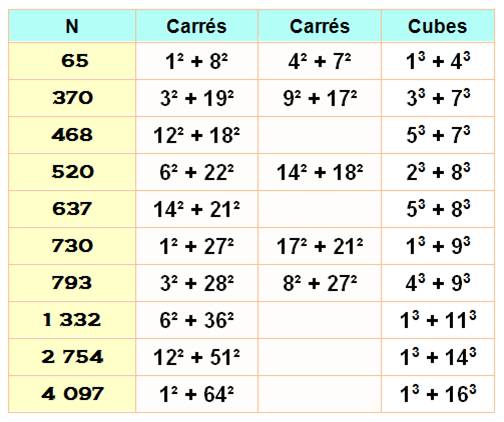
Un nombre est somme de deux cubes selon ces trois conditions. Avec exemple à droite.	Il existe un diviseur m de N compris entre racine cubique de N, et racine cubique de 4N	N = 65 = 1^3 + 3^3 m = 5, un diviseur de N
	Il existe k, un entier positif, tel que:
		25 – 4 x 4 = 9 = 3²

N = Somme de trois nombres (+ ou -) au cubes
Première valeur conséquente pour 16.			16 = (–511)^3 + (–1609)^3 + (1626)^3
Longtemps, on n'a pas su écrire 30 sous la forme de trois cubes.			30 = 2 220 422 932^3 + (–2 218 888 517)^3 + (–283 059 965)^3
On se sait toujours pas si 33, 42, 74, 114, 165, 627, 633, 732, 795, 906, 921, 975 sont sommes de trois cubes.			Testé jusqu'à 10^42 Voir site: How to search the solutions of n = x^3 + y^3 + z^3 – Hisanori Mishima
Tout nombre de la forme n'est pas somme de trois cubes.		Un cube est divisible par 9 ou divisible par 9 à 1 près: Somme de trois cubes Pas de 4! Donc pas de la forme indiquée.
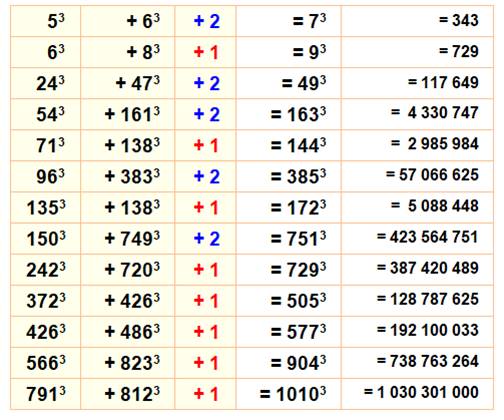
Famille de solutions:	(9n^3 + 1)^3 + (9n^4)^3 + (–9n^4 – 3n)^3 = 1 729n^3+243n^6+27n^3+1+729n^12–729n^12–729n^9–243n^6–27n^3 Ex : pour n = 2 => 389 017^3 + 2 985 984^3 – 3 375 000^3 (6n^3 + 1)^3 – (6n^3 – 1)^3 – (6n^2)^3 = 2 216n^9+108n^6+18n^3+1-216n^9+108n^6-18n^3+1-216n^6 = 2 Ex : pour n = 2 => 117 649^3 – 103 823^3 – 13 824^3

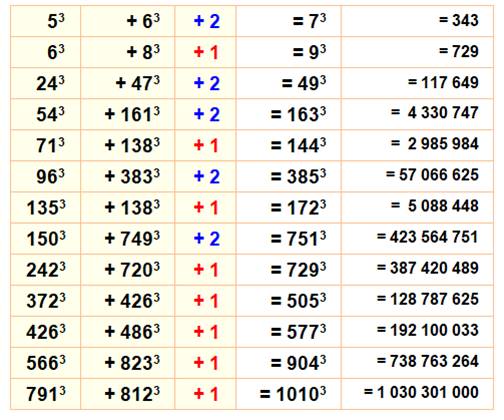
Voir Table de ces sommes pour n de 1 à 100

SOMME de n CUBES, plusieurs fois
2 cubes 2 fois	1 729 le plus petit entier décomposable de deux façons en somme de deux cubes.	1729 = 1^3 + 12^3 = 9^3 + 10^3 = 1 + 1728 = 729 + 1000 Voir Table des sommes de deux cubes deux fois Voir 1729 et histoire à propos de ce nombre Voir Calcul de cubes de nombres consécutifs
2 cubes 3 fois	87 539 319 le plus petit nombre décomposable en 3 sommes de 2 cubes. 175 959 000 est le second connu.	87 539 319 = 167^3 + 436^3 = 228^3 + 423^3 = 255^3 + 414^3 175 959 000 = 70^3 + 560^3 = 315^3 + 525^3 = 198^3 + 552^3
2 cubes n fois	Nombres TAXICAB Le plus petit nombre qui est somme de n fois deux cubes. etc. SUITE en NOMBRES TAXICAB
3 cubes 2 fois	251 le plus petit nombre décomposable en 2 sommes de 3 cubes.	251 = 1^3 + 5^3 + 5^3 = 1 + 125 + 125 = 2^3 + 3^3 + 6^3 = 8 + 27 + 216
4 cubes 2 fois		81 = 0^3 + 3^3 + 3^3 + 3^3 = 1^3 + 2^3 + 2^3 + 4^3

Voir Nombre = sommes de cubes

Somme de cubes et sommes de carrés

Il est possible de créer autant de couples que l'on veut.

Avec la relation a² + b² = c³ + d³ , en multipliant par 64 = 4³

(4c)³ + (4d)³ = 64(c³ + d³) = 64 (a² + b²) = (8a)² + (8b)²

8² + 64² = 4³ + 16³ = 4 160

Un double couple (le plus petit, sans doute).

4 624 776 = 1 026² + 1 890² = 1 350² + 1 674² = 51³ + 165³ = 72³ + 162³

CUBE = SOMME de CUBES
		a^3 + b^3 = c^3 N'existe pas: théorème de Fermat-Wiles. a^3 + b^3 = 2c^3 De même pour la somme de deux cubes, double d'un cube.
Cube, presque somme de 2 cubes à 1 ou 2 près Avec 1 = 1^3 il s'agit d'une somme de 3 cubes
Cube, somme de 3 ou 4 cubes
Par combinaison

Voir Cubes =somme de cinq cubes / Pépites / Quadruplets / Table des sommes de cubes / Énigme de la pesée des quatre cubes

Diconombre: 216 / 729 / 8 000

Somme de cubes

2^3 + 2^3 = 2 x 2^3 = 2^4 3^3 + 3^3 + 3^3 = 3 x 3^3 = 3^4 4^3 + 4^3 + 4^3 + 4^3 = 4 x 4^3 = 4^4 ^… n^3 + n^3 + … + n^3 = n x n^3 = n^4

9^3 + 18^3 = 9^4 28^3 + 84^3 = 28^4 65^3 + 260^3 = 65^4 …

CARRÉ = SOMME de CUBES

Carré somme de 2 cubes

Exemple

24² = 4³ + 8³

Toutes les valeurs jusqu'à 100

a 1 2 2 4 7 8 9 10 11 14 16 18 22 25 28 32 33 36 49 50 56 65 72 98

b 2 2 46 8 21 8 18 65 37 70 32 18 26 50 84 32 88 72 98 50 65 91 72 98

c 3 4 312 24 98 32 81 525 228 588 192 108 168 375 784 256 847 648 1 029 500 671 1 014 864 1 372

a^3 1 8 8 64 343 512 729 1 000 1 331 2 744 4 096 5 832 10 648 15 625 21 952 32 768 35 937 46 656 117 649 125 000 175 616 274 625 373 248 941 192

b^3 8 8 97 336 512 9 261 512 5 832 274 625 50 653 343 000 32 768 5 832 17 576 125 000 592 704 32 768 681 472 373 248 941 192 125 000 274 625 753 571 373 248 941 192

c^2 9 16 97 344 576 9 604 1 024 6 561 275 625 51 984 345 744 36 864 11 664 28 224 140 625 614 656 65 536 717 409 419 904 1 058 841 250 000 450 241 1 028 196 746 496 1 882 384

Voir: Méthode de calcul

Somme des entiers au cube = carré de la somme de ces entiers

Double d'un carré somme de 2 cubes

En bleu les configuration triviales du type: (n²)³ + (n²)³ = 2 x (n³)²

Carré somme de 3 cubes

Exemple

(1 + 2 + 3)² = 6² = 1³ + 2³ + 3³

Voir Carré somme de cubes avec nombres consécutifs

Toutes les valeurs jusqu'à 20

a 1 1 1 1 1 2 3 4 4 6 6 6 8 8 9 10 12 12

b 2 2 4 6 14 9 3 4 8 9 10 14 9 13 14 10 12 17

c 3 6 14 8 19 14 3 17 12 16 20 16 19 15 16 20 12 20

d 6 15 53 27 98 59 9 71 48 71 96 84 90 78 87 100 72 121

a^3 1 1 1 1 1 8 27 64 64 216 216 216 512 512 729 1 000 1 728 1 728

b^3 8 8 64 216 2 744 729 27 64 512 729 1 000 2 744 729 2 197 2 744 1 000 1 728 4 913

c^3 27 216 2 744 512 6 859 2 744 27 4 913 1 728 4 096 8 000 4 096 6 859 3 375 4 096 8 000 1 728 8 000

d^2 36 225 2 809 729 9 604 3 481 81 5 041 2 304 5 041 9 216 7 056 8 100 6 084 7 569 10 000 5 184 14 641

Carré somme de 4 cubes

Exemple

100 = 1³ + 2³ + 3³ + 4³

= (1 + 2 + 3 + 4)²

Voir Carrés et cubes

Toutes les valeurs jusqu'à 10

a 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 3 4 4 4 4 4 5 9

b 1 2 2 2 2 2 2 2 2 3 4 8 2 2 2 2 3 6 7 4 4 6 6 8 6 9

c 1 2 2 2 3 4 6 6 8 3 8 8 2 4 5 6 9 7 7 4 8 6 8 8 6 9

d 1 2 4 8 4 6 6 10 10 9 8 10 10 4 7 9 10 9 8 4 9 9 9 8 7 9

e 2 5 9 23 10 17 21 35 39 28 33 45 32 12 22 31 42 36 35 16 37 35 39 40 30 54

a^3 1 1 1 1 1 1 1 1 1 1 1 1 8 8 8 8 8 8 27 64 64 64 64 64 125 729

b^3 1 8 8 8 8 8 8 8 8 27 64 512 8 8 8 8 27 216 343 64 64 216 216 512 216 729

c^3 1 8 8 8 27 64 216 216 512 27 512 512 8 64 125 216 729 343 343 64 512 216 512 512 216 729

d^3 1 8 64 512 64 216 216 1 000 1 000 729 512 1 000 1 000 64 343 729 1 000 729 512 64 729 729 729 512 343 729

e^2 4 25 81 529 100 289 441 1 225 1 521 784 1 089 2 025 1 024 144 484 961 1 764 1 296 1 225 256 1 369 1 225 1 521 1 600 900 2 916

CUBES de NOMBRES CONSÉCUTIFS
Cubes consécutifs	9 seul carré somme de cubes de nombres consécutifs.	9 = 3² = 1^3 + 2^3
Parfaits	Tout nombre parfait, sauf 6, est décomposable en somme de cubes d'impairs successifs.	28 = 1^3 + 3^3 496 = 1^3 + 3^3 +5^3 + 7^3
Divisible	La somme des cubes de trois nombres consécutifs est divisible par 9.	9 | (n-1)^3 + n^3 + (n+1)^3 Rappel La barre verticale se lit "divise"

CURIOSITÉS

Distincts

12 758

est le plus grand nombre qui ne peut pas s'écrire comme la somme de cubes distincts.

Chiffres

Seuls 6 nombres sont égaux à la somme des chiffres de leur cube.

n	n^3
1	1
8	512
17	4 913
18	5 832
26	17 576
27	19 683

Seuls 4 nombres sont égaux à la somme des cubes de leurs chiffres.

n	Cubes des chiffres
153	1 + 125 + 27
370	27 + 343
371	27 + 343 + 1
407	64 + 343

Boucle rare

Unique solution

pour 2, 3 ou 4 chiffres et

pour les puissances 2, 3, 4

au moins

1 3 6 = 2³ + 4³ + 4³

2 4 4 = 1³ + 3³ + 6³

Les deux plus proches à 2 près:

24 = 2³ + 2³ + 2³

224 = 2³ + 6³

155 = 3³ + 4³ + 4³

342 = 1³ + 5³ + 6³

Somme de cubes et concaténation

La concaténation des nombres est égale à la somme des cubes

41833 = 4³ + 18³ + 33³

165033 = 16³ + 50³ + 33³

221859 = 22³ + 18³ + 59³

336701 = 33³ + 67³ + 01³

341067 = 34³ + 10³ + 67³

407001 = 40³ + 70³ + 01³

444664 = 40³ + 46³ + 64³

487215 = 48³ + 72³ + 15³

982827 = 98³ + 28³ + 27³

983221 = 98³ + 32³ + 31³

1000407 = 100³ + 04³ + 07³

1001001 = 100³ + 10³ + 01³

Liste des sommes des puissances des cubes de nombres consécutifs

S2 est la somme de 2 cubes. Ex: 35 = 2³ + 3³

S3 est la somme de 3 cubes. Ex: 99 = 2³ + 3³ + 4³

Florilège de cubes

100	= 1^3 + 2^3 + 3^3 + 4^3	Somme de 4 cubes consécutifs
8 000	= 2^6 x 5^3 = 20^3 = 7^3 + 14^3 + 17^3 = 11^3 + 12^3 + 13^3 + 14^3	Cube Somme de 4 cubes consécutifs Somme de 3 cubes
9 000	= 10^3 + 11^3 + 12^3 + 13^3 + 14^3	Somme de 5 cubes consécutifs
16 830^3	= 1134^3 + 1135^3 +1136^3 + … + 2133^3	Cube Somme de 1000 cubes consécutifs

8000 & 16830³ sont cités page 345 du livre "Code to Zero" de Ken Follet

Somme de deux cubes bien en forme!

Nombres somme de deux cubes et égal à une opération avec les chiffres de ces nombres au cube. Les six premières lignes son uniques avec le deuxième cubes à un seul chiffre. Ils sont 28 lorsque le deuxième cube comporte deux chiffres. Ici, tous ceux jusqu'à 10 000 pour le multiplicateur objet de la troncature. Voici des exemples typiques pour trois chiffres (il y en a 6 jusqu'à 5 millions). Avec quatre chiffres (exemples, il y en a 19 jusqu'à 50 millions) Remarquez la présence répétitive de 333, 667, 668.

Voir Nombres en formes

Suite	Problème de la somme des trois cubes Sommes de cubes – Table de 1 à 1000 Puissances 4, 5 … Somme de cubes Somme de cubes 2 fois
Voir	Bi, tripartitions Carré des triangulaires = somme de cubes Cubes Nombre = sommes de cubes Nombre = sommes de puissances Nombres = somme multiples de puissances (Orientation parmi toutes les formes de sommes de puissances) Nombres carrés Nombres cubes Nombres polygones Nombres triangles Somme multi puissantes Table des puissances des nombres Unité des puissances
DicoNombre	Nombre 19 683 = 27^3
Sites	The Fifth Taxicab Number is 48988659276962496 – David Wilson OEIS A011541 – Taxicab Numbers that can be expressed as the sum of two cubes in exactly two different ways – Mathematics – Forum Characterizing the Sum of Two Cubes – Kevin Broughan – 2001 Integers equal to the sum of three cubes – Chaitanya
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/Partiti2.htm