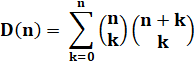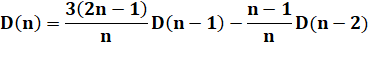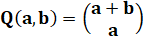|
Édition du: 09/07/2023 |
|
INDEX |
Types de Nombres – GRILLES |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Nombres de DELANNOY & nombres de SCHRÖDER
On dira grille
ou réseau ou quadrillage ou même échiquier. Ici, il s'agit
d'une grille rectangulaire sur la quelle les mouvements peuvent être
effectués:
En 1886, Henri Delannoy (1833-1915) publie: Emploi de
l'échiquier pour la solution de problèmes arithmétiques. Ernst Schröder (1841-1902) est connu pour ses
travaux sur l'algèbre, la théorie des ensembles et la logique. |
||
|
|
Sommaire de cette page >>> Approche: grille 2 × 2 >>> Grille 4 × 4 >>> Nombres de Delannoy >>> Nombres de Schröder >>> Chemins dans un réseau >>> Anglais |
Débutants Glossaire |
|
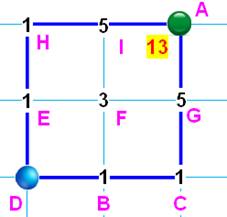
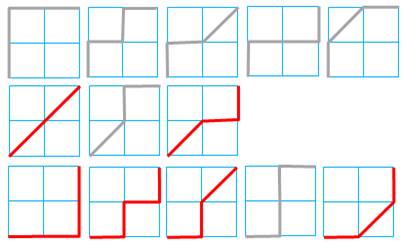
Parcourir la grille Une grille carrée de 2 × 2, par exemple. Chemins permis: aller à droite, en haut ou en
diagonale vers le haut droit. Sur cette grille, il s'agit de partir du point D
(départ) et rejoindre le point A (arrivée). Combien de chemins possibles ? Dénombrement Pour aller au point B: un seul chemin; idem pour
C, E et H. Pour aller en F, il faut passer par B (1 chemin)
ou par E (1 chemin) ou aller en diagonale (1 chemin). Soit trois
possibilités. On note ce compte pour F. Pour aller en G, il faut passer par C (1 chemin)
ou par F (3 chemins) ou en diagonale depuis F (1 chemin) Total: 1 + 3 + 1 =
5; idem pour I. Pour aller en A, on compte: 5 + 5 + 3 = 13
chemins possibles. |
|
||
|
Les trois chemins pour rejoindre
le point F |
|
||
|
Les treize chemins pour rejoindre
le point A |
|
||
|
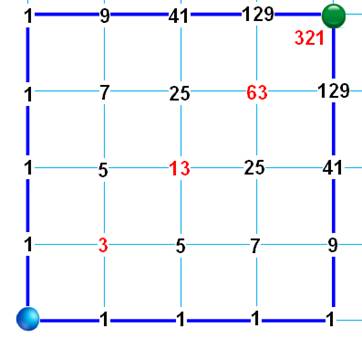
Dénombrement Selon la méthode pas à pas vue ci-dessus. Pour chaque point de la grille, on compte la somme
des chemins des trois voies pour y arriver, à gauche; en dessous et en
diagonale gauche-bas. Pour la grille 2 × 2, on retrouve naturellement le décompté précédent: 13. Pour la grille 3 × 3, on aura: 63. Pour la grille 4 × 4, on aura: 321 |
|
|
Les 63 chemins pour une grille 3 × 4

Source image: Delannoy, Schröder, and Motzkin Numbers – Robert Dickau
|
Formulation explicite Avec les coefficients
binomiaux |
|
||
|
Formulation récurrente (n>1) |
|
||
|
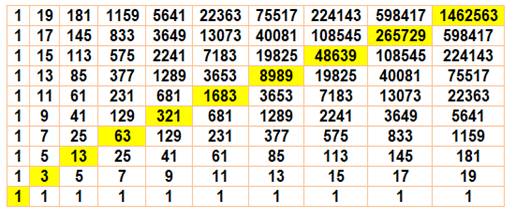
Nombres de Delannoy |
1, 3, 13, 63, 321, 1683, 8989, 48639,
265729, 1462563, 8097453, 45046719, 251595969, 1409933619, 7923848253,
44642381823, 252055236609, 1425834724419, 8079317057869, 45849429914943,
260543813797441, 1482376214227923, 8443414161166173, 48141245001931263, … |
||
|
Matrice de Delannoy Disposition rectangulaire qui peut très bien être mise en triangle à
la manière du triangle
de Pascal. On aurait: 1 1 1 1 3 1 1 5 5 1 … |
|
||
|
Définition Ils comptent les chemins de Delannoy contenus
exclusivement dans le triangle isocèle-rectangle bas-droit (autrement dit :
aucun point au-dessus de la droite y = x. Grille 2 × 2 Le graphique montre la sélection des six chemins
de Schröder parmi les treize de Delannoy. |
|
||
|
Nombres de Schröder |
1, 2, 6, 22,
90, 394, 1806, 8558, 41586,
206098, 1037718, 5293446, 27297738, 142078746, 745387038, 3937603038,
20927156706, 111818026018, … |
||
|
Réseau (anglais: lattice) On se donne une grille, un quadrillage, formé de
points dont on précise les coordonnées (a, b) Un chemin nord-est part du coin bas-gauche de
coordonnées (0, 0). Sa trajectoire passe de point en point de la grille en
progressant vers le nord ou vers l'est (pas en diagonale) |
Quantité de chemins nord-est Pour aller du point origine au point (a, b) du
réseau, il existe Q chemins, avec:
|
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
||