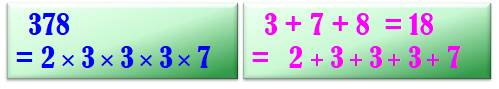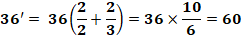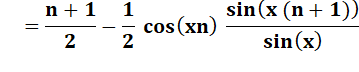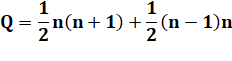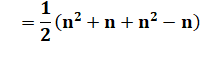NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/06/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 20		Page 40		Page 50		Page 60			Page 70
	Page 60 (1180-1199)		Page 61 (1200-1219)		Page 62 (1220-1239)		Page 63 (1240-1259)		Page 64 (1260-1279)
	Page 65 (1280-1299)		Page 66 (1300-1319)		Page 67 (1320-1339)		Page 68 (1340-1359)		Page 69 (1360-1379)

BRÈVES de MATHS – Page 62

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

1220. Vocabulaire des maths
Rigueur et précision Les mathématiques nécessitent de la rigueur pour émettre des hypothèses, conduire un raisonnement et exprimer des conclusions. La condition de la réussite tient essentiellement à la précision du vocabulaire utilisé.		Où se renseigner sur ce site ? Mots principaux selon le niveau d'étude >>> Jargon des maths démystifié >>> Mots des maths expliqués aux débutants >>> Dictionnaire de base du vocabulaire des mathématiques (DicoMot Math) >>>
Brèves associées	>>> Orthographe des nombres		>>> Brèves Langue – Index
Pour en savoir plus	>>> Langues – Index		>>> Enseignement – Index

1221. Jargon de l'école
Adjacent	Collé à côté; qui ont un côté en commun.
Aire	Surface ou superficie	>>>
Algorithme	Recette de calcul; description pas à pas d'une méthode pour obtenir quelque chose.	>>>
Circonférence	Le tour du cercle, son périmètre	>>>
Coordonnées	Nombres qui définissent un point. Analogie avec la définition d'une case dans une grille.	>>>
Plan	Analogie avec une feuille de papier (deux dimensions). Par opposition à l'espace (trois dimensions)	>>>
Quotient	Résultats de la division. Exemple: 5 est le quotient de la division 10 / 2.	>>>
Somme / Différence	Résultat de l'addition et de la soustraction.	>>>

1222. Jargon du collège
Affine	Qui évolue de façon proportionnelle, linéaire.	>>>
Aléatoire	Au hasard	>>>
Champ	Caractérise la propriété en chaque point d'un plan ou d'un espace Comme le champ magnétique dont l'intensité et la direction varie en tout point.	>>>
Ensemble	Collection de choses, d'éléments.	>>>
Homothétie	Transformation qui grossit une figure (ou l'inverse). Le rapport d'homothétie précise le facteur de grossissement. Homothétiques: qui sont semblables	>>>
Isométriques	Qui ont même mesure, même longueur; qui sont égaux	>>>
Orthogonal	Perpendiculaire.	>>>
Scalaire	Un nombre normal. Utilisé dans le monde des vecteurs.	>>>
Symétrie	Effet miroir qui produit une image inversée de l'original.	>>>
Théorème	Propriété démontrée une fois pour toute. Le lemme est un "petit" théorème souvent provisoire.	>>>
Translation	Glissement sans faire tourner	>>>
Trigonométrie	Calculs dans les triangles: côtés et angles	>>>

1223. Jargon du lycée
Isobarycentre	Centre de gravité Pour un objet mathématique ou un objet physique homogène (centre de masse)	>>>
Complexe	Un tout formé de deux nombres: un réel et un imaginaire Le couple représente les coordonnées d'un point du plan.	>>>
Déterminant	Somme de produit dans le calcul des matrices	>>>
Discret	Contraire de continu Valeur qui progresse par bonds	>>>
Discriminant	Terme général pour la résolution des équations Sa valeur détermine la nature des racines	>>>
Ensemble quotient	On pourrait dire ensemble partagé selon les restes de la division	>>>
Groupe	Ensemble d'éléments considéré comme un tout. Un objet mathématique qui possède des propriétés particulières.	>>>
Imaginaire	Nombre annoncé par le nombre i tel que i² = –1	>>>
Isomorphisme	Correspondance un à un entre deux ensembles.	>>>
Matrice	Tableau de nombres considéré comme un tout.	>>>
Norme	Longueur d'un vecteur.	>>>
Tenseur	Une généralisation des vecteurs.	>>>
Vecteur	Une flèche représentant un déplacement ou une force	>>>

Suite en DicoMot Math

1224. Méthode de Newton
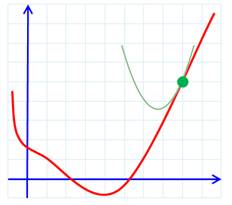
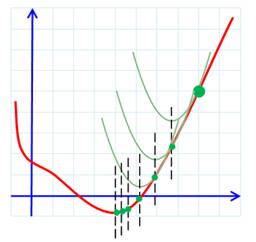
Actualités En mi-2024, (publication 2025 par les journaux) trois mathématiciens inventent un algorithme améliorant la méthode de recherche de solutions dite de Newton en l'étendant aux équations de degré élevé et multivariables. Comment fonctionne la méthode de Newton, en bref ? La fonction est représentée par la courbe rouge. À l'œil, le minimum est évident, mais pour un ordinateur ? La méthode consiste à choisir (estimation, intuition !) un point sur la courbe (vert). On cherche la courbe simple (ici une parabole en vert) qui approxime au mieux la courbe dans le voisinage du point. On note le point bas de la parabole et on reporte ce point sur la courbe (en abscisse, pointillé noir). C'est un nouveau point qui s'approche de la solution (vert) On recommence la procédure avec ce nouveau point vert et ainsi de suite jusqu'à converger vers un point stable, le point cherché.			Illustration
Brèves associées	>>> Complexité algorithmique	>>> Brèves Algorithme – Index
Pour en savoir plus	>>> Méthode de Newton	>>> Algorithme

1225. Nombres miroirs
Nombre miroir: nombre a à la puissance b se terminant par les nombres a suivi de b. Ils sont une douzaine jusqu'à 10 000. Le nombre 499 est exceptionnel avec la répétition (a = b).
Brèves associées	>>> Chiffres dans les puissances de 2		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Nombres miroirs		>>> Automorphismes

1226. Nombre 378 et ses facteurs
Somme des chiffres du nombre = somme des facteurs du nombre (autant qu'ils sont)
Somme (presque !)des cubes du nombre = somme des cubes des facteurs uniques.
Brèves associées	>>> Nombre 333		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre 378		>>> DicoNombre – Index

1227. Dérivée Numérique
Dérivée numérique On sait dériver les fonctions. Mais, sait-on dériver des nombres? Oui, en utilisant la factorisation des nombres. Technique proposée en 1911 par le mathématicien espagnol Josè Mingot Shelly. À quoi cela sert-il ? Un autre outil à la disposition des chercheurs en théorie des nombres. Notamment pour résoudre des conjectures qui résistent encore. Règles de construction La construction est simple: on donne la valeur 1 à tous les nombres premiers. Puis, les nombres composés n = a∙b sont construits en utilisant la règle (prime désigne la dérivée): n' = a ∙ b' + a' ∙ b		Exemples Premier: 7 = 1 × 7 => 7' = 1 Carré: 4 = 2 × 2 => 4' = 2 × 2' + 2' × 2 = 2 × 1 + 1 × 2 = 4 Composé: 20 = 4 × 5 => 20' = 4 × 5' + 4' × 5 = 4 × 1 + 4 × 5 = 24 Calcul direct avec un exemple La dérivée est égale au nombre multiplié par la somme des fractions où chacune est l'exposant divisé par le facteur. Ainsi:2² devient 2/2 et 3² devient 2/3.
Brèves associées	>>> Dérivée et intégrale (simplement !)		>>> Brèves Analyse – Index
Pour en savoir plus	>>> Dérivée numérique		>>> Dérivées

1228. Nombre 364
Somme de triangulaires Le nombre 364 est la somme des douze premiers nombres triangulaires. Le nombre triangulaire de rang n est la somme de tous les nombres de 1 à n. Chaque ligne du tableau est l'un d'entre eux avec la somme à droite. Ainsi T3 = 1 + 2 + 3 = 6. En additionnant tous ces nombres, la somme est 364. Somme des douze premiers nombres triangulaires		Comptine: les douze jours de Noël Chaque couplet énumère un objet de plus que le précédent. Douzième couplet: Le douzième jour de Noël J'ai reçu de mon ami Douze ventouses Onze pierres ponces Dix bigoudis Neuf bonnets neufs Huit parapluies Sept pincettes Six poésies Cinq gros poussins Quatre pissenlits Trois petites poules Deux caramels Et un moineau tout en haut du pommier Décompte En comptant les objets énumérés le long des douze couplets, la comptine compte 364 objets.
Brèves associées	>>> Nombre 333		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre 364		>>> Chansons et poésies

1229. Intersections dans l'octogone
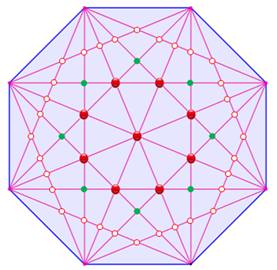
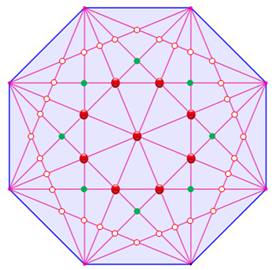
Un octogone quelconque possède 20 diagonales. Ces diagonales se croisent à l'intérieur de l'octogone. Dans le cas général, il y a 70 points d'intersections. Avec un octogone régulier, les diagonales se croisent parfois en un même point. C'est le cas des points rouges sur la figure. Dans ce cas, il y a seulement 49 points d'intersections. Autant le calcul dans le cas des polygones quelconques est simple (quantité de combinaisons de 4 parmi n), autant il est très délicat dans le cas du polygone régulier. La formule est extrêmement compliquée !		Octogone régulier et intersections des diagonales
Brèves associées	>>> Octogone – Diagonales		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Intersections dans les polygones		>>> Régions dans les polygones

1230. Calcul d'une somme trigonométrique
Méthode du changement de monde Comment s'y prendre pour calculer une telle somme de sinus au carré ? Oui, cela n'est pas évident ! Comme on le pratique souvent en maths, la solution consiste à changer de monde (principe du levier mathématique). En l'occurrence: à passer dans le mondes des exponentielles pour y réaliser la partie calculatoire. Pour cela, on utilise les formules d'Euler. Le retour au monde trigonométrique s'effectue en inversant les formules d'Euler.		Ce qu'il faut trouver
Principe du calcul
Brèves associées	>>> Somme de produits		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Calcul de somme de sinus >>> Calcul de somme de sinus au carré		>>> Formules d'Euler >>> Principe du levier mathématique

1231. Nombres et leurs chiffres
Quels sont les relations de divisibilité entre un nombre donné et ses chiffres ?
Il est divisible par chacun de ses chiffres (nombre nu)		224 = 2 × 112 = 4 × 56
Idem avec chiffres tous différents (Lynch-Bell)		248 = 2 × 124 = 4 × 62 = 8 × 31
Idem mais avec un reste de 1 (Chiffres mod 1)		289 = 2 × 144 + 1 = 8 × 36 + 1 = 9 × 32 + 1
Il est divisible par les chiffres des extrémités (fourchette)		104275 = 1075 × 97
Il est divisible par la somme de ses chiffres (Harshad)		198 = (1+9+8) × 11 = 18 × 11
Il est divisible par le produit de ses chiffres (Zuckerman)		384 = (3×8×4) × 4 = 96 × 4
Il est divisible par la somme et produit du carré ses chiffres (nombre insolite)		122 121 216 = 56 × 2 180 736 = 9 216 × 13 251
Brèves associées	>>> Nombres fourchettes	>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Nombres de Harshad et autres	>>> Nombres et chiffres – Index

1232. Cycle 123
Propriété du nombre 123 Ce nombre comporte: 1 chiffre pair; 2 chiffres impairs; et 3 chiffres au total. Ces nombres pris dans l'ordre recomposent le nombre initial.
Cycle 123 Chaque nombre est transformé en un autre nombre composé de la façon suivante: le premier chiffre indique la quantité de chiffres pairs; le deuxième, la quantité de chiffres impairs; et le troisième, la quantité de chiffres dans le nombre. Le procédé est répété jusqu'à obtenir le nombre 123, toujours présent.
Brèves associées	>>> Cycle Syracuse ou Collatz ou 3x + 1		>>> Brèves Itérations – Index
Pour en savoir plus	>>> Cycle 123		>>> Cycles – Index

1233. Triangle de Pascal et 11
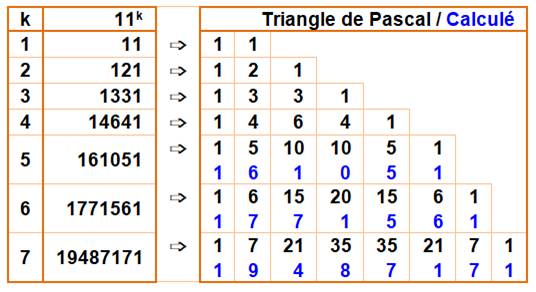
Puissances de 11 et triangle de Pascal Prenez les lignes du triangle Pascal, ce sont les puissances successives de 11, à condition de calculer chaque chiffre en reportant les dizaines.
Brèves associées	>>> Triangle de Pascal – Nombres 1, 3, 3, 1	>>> Brèves Itérations – Index
Pour en savoir plus	>>> Triangle de Pascal et puissances de 11	>>> Nombre 1

1234. Quel chemin ?
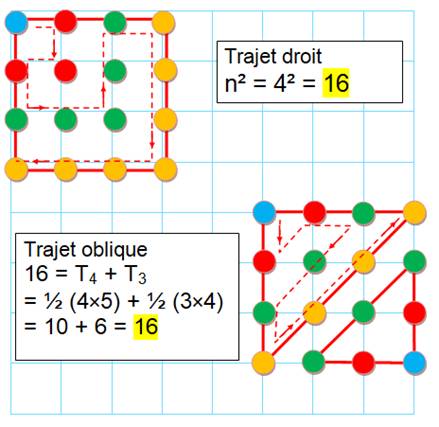
Droit ou oblique ? Il s'agit de compter les points d'un quadrillage. Deux possibilités: Trajet droit de gauche à droite et de haut vers le bas. Trajet oblique ou en diagonale. Comparaison ?		Trajet droit On remarque immédiatement qu'il s'agit de la somme des nombres impairs, laquelle est égale à un carré. Trajet oblique Cette fois, on reconnait la somme des nombres successifs, laquelle est un nombre triangulaire; la somme vaut ½ n(n + 1). Pour parcourir l'ensemble des points, il faut poursuivre avec un triangle plus petit d'une unité.
				Calcul du cas oblique
Brèves associées	>>> Points dans le carré		>>> Brèves Compter – Index
Pour en savoir plus	>>> Somme des nombres entiers		>>> Somme des nombres impairs

1235. Peinture à deux
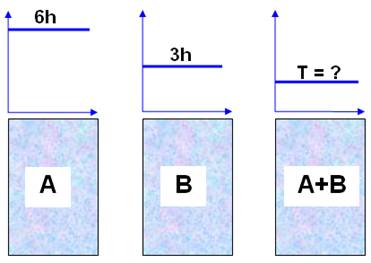
Question Un mur est peint en 6 heures par Albert et en 3 heures par Bernard. Ils se mettent à peindre ensemble. En combien de temps peignent-ils le mur ? Commentaires À deux, il faudra moins de temps que le plus rapide, donc moins de 3 heures. Bernard, le plus rapide, va deux fois plus vite qu'Albert. Chaque fois qu'Albert peint une tranche, Bernard peint deux tranches.		Illustration
Résolution par raisonnement En une heure, quel est le travail réalisé ? Ce sont des fractions de mur: 1/6 pour Albert et 1/3 par Bernard.		À deux, en une heure, ils peignent la somme 1/6 + 1/3 = 1/2. Donc la moitié du mur. Il leur faudra donc 2 heures pour peindre le mur complet.
Brèves associées	>>> Fractions et produits		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Peinture à deux		>>> Problèmes de vitesse – Index

1236. Poules et œufs en demis
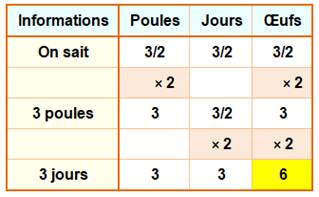
Énigme Le fermier facétieux constate qu'en moyenne: une poule et demie pond un œuf et demi en un jour et demi. Il demande plein de malices: combien pondent trois poules en trois jours ? Piste Comprendre que si on double le nombre de poules, il y aura deux fois plus d'œufs dans le même temps. Si on double le temps, il y aura deux fois plus d'œufs avec le même nombre de poules. Si on double la quantité de poules et la quantité de jours, il y aura quatre fois plus d'œufs.		Solution Un tableau permet de suivre cette relation bilinéaire.
Brèves associées	>>> Œufs dans le panier		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Poules et œufs et demis		>>> Énigmes et Jeux – Index

1237. Nombre auto-descriptif
6210 001 000		Nombre qui se compte lui-même dit auto-descriptif. Ce nombre original est tel que chaque chiffre indique la quantité de chiffres de son rang: Six 0, deux 1, un 2, zéro 4, etc. Notez que la somme des 10 chiffres est 10, ce qui est une condition pour être auto-descriptif. Les auto-descriptifs typiques sont sept en base 10, mais il est possible d'en former une infinité sur la base de celui présenté ici.
Brèves associées	>>> Nombres auto-descriptifs		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Nombre 6,2… 10^9 >>> Fréquence des chiffres dans un nombre			>>> Auto-descriptif

1238. Nombre à facteurs consécutifs
Tout nombre se factorise de manière unique: tout nombre est le produit de nombres premiers de plus en plus grands et cela d'une seule manière. Quels sont les nombres pour lesquels au moins trois des facteurs sont des nombres premiers qui se suivent ? La liste est finalement assez longue. Ils sont 40 jusqu'à 1000: 30, 60, 90, 105, 120, 150, 180, 210, 240, 270, 300, 315, 330, 360, 385, 390, 420, 450, 480, 510, 525, 540, 570, 600, 630, 660, 690, 720, 735, 750, 770, 780, 810, 840, 870, 900, 930, 945, 960, 990.		Factorisation de 990 Les facteurs sont: 2, 3, 5 et 11. Liste des plus petits nombres premiers 2, 3, 5, 7, 11, 13 … Comparaison Le nombre 990 a bien trois facteurs premiers consécutifs. C'est le plus grand à trois chiffres.
Brèves associées	>>> Nombres abondants, déficients et parfaits		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres à K premiers consécutifs >>> Théorème fondamental de l'arithmétique		>>> Facteurs – Index >>> Nombres premiers

1239. Cobordisme (topologie)
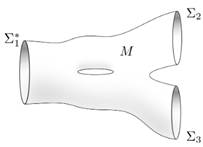
Pantalon Une image classique pour illustrer le cobordisme est celle du pantalon topologique : imaginez un pantalon dont la taille représente une surface et dont les deux jambes représentent une autre surface. Le pantalon lui-même est un cobordisme entre la surface-taille et les surfaces-jambes. Variétés Pour simplifier traduire variété par surface, mais de dimensions quelconques. 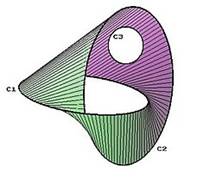L'étude des variétés pour les grandes dimensions est complexe. Le cobordisme permet de simplifier leur étude. Cobordime Deux variétés sont reliées par un cobordisme s'ils forment ensemble la bordure d’un espace de dimension supérieure. Hypothèse du Cobordisme Elle affirme que pour une théorie quantique topologique, connaître le comportement de la théorie sur le cas le plus simple – un point – permet de comprendre et de reconstruire toute la théorie sur des objets plus complexes.		Image du pantalon Illustration du cobordisme simple Un cobordime plus élaboré
Brèves associées	>>> Voirie minimale – Arbre de Steiner		>>> Brèves Topologie – Index
Pour en savoir plus	>>> Cobordisme		>>> Variétés

Retour	Brèves de maths – Page 52
Suite	Brèves de maths – Page 63
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve62.htm