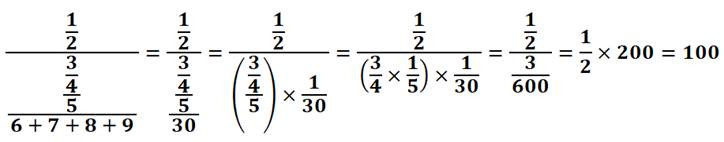NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/09/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 20		Page 40		Page 50		Page 60			Page 70
	Page 60 (1180-1199)		Page 61 (1200-1219)		Page 62 (1220-1239)		Page 63 (1240-1259)		Page 64 (1260-1279)
	Page 65 (1280-1299)		Page 66 (1300-1319)		Page 67 (1320-1339)		Page 68 (1340-1359)		Page 69 (1360-1379)

BRÈVES de MATHS – Page 63

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

1240. Voyage vers l'étoile la plus proche
Proxima du Centaure La plus proche étoile de notre Système solaire est Proxima Centauri. Cette naine rouge fait partie du système Alpha Centauri. Elle se trouve à 4,244 années-lumière (al) du Système solaire, soit 270 000 unités astronomiques (ua). Cela correspond à environ 40 000 milliards de kilomètres (4 10^13 km). Durée du voyage vers cette étoile La sonde New Horizons, la plus rapide actuellement, se déplace à environ 17 km/s. Elle mettrait 78 000 ans pour atteindre cette étoile.		Qui existait sur Terre il y a environ 100 000 ans ? Un humain arrivant aujourd'hui sur Proxima serait un hominidé du Pléistocène, une période du Quaternaire marquée par d’importantes fluctuations climatiques. La Terre était alors le théâtre d’une grande diversité d'Hominidés, résultat d’un long processus évolutif qui a mené progressivement à l’émergence de l’Homme moderne. Principaux groupes présents à cette époque Homo sapiens: présent en Afrique il y a environ 200 000 à 300 000 ans; des groupes sont en route pour coloniser le globe; Homo neanderthalensis (Néandertaliens) en Europe et Asie occidentale. Ils dominent car robustes et bien adaptés aux climats froids; et Les Denisoviens en Asie, peuple moins bien connus car peu de fossiles.
Brèves associées	>>> Lumière – Vitesse limite		>>> Brèves Sciences – Index
Pour en savoir plus	>>> Étoiles: Proxima Centauri >>> Système solaire – Planètes		>>> Année-lumière >>> Ères géologiques >>> Hominidés

1241. Respiration et pression
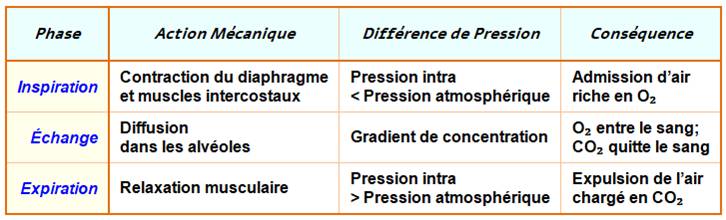
Attention ! Nous n'aspirons pas de l'air en respirant; nous faisons de la place dans la cage thoracique pour que l'air, sous l'effet de la pression atmosphérique, s'engouffre dans nos poumons. Nos poumons sont comme une poche molle. Pas de muscles.		Mécanisme de la respiration L’inspiration est associée à une augmentation du volume de la cage thoracique, une diminution de la pression dans les poumons et une entrée de l’air de l’extérieur vers les poumons. L’expiration est associée à une diminution du volume de la cage thoracique, une augmentation de la pression dans les poumons et une sortie de l’air des poumons vers l’extérieur.
En résumé
Brèves associées	>>> Nanotechnologies		>>> Brèves Sciences – Index
Pour en savoir plus	>>> Respiration humaine		>>> Pression

1242. Chirurgie topologique
Principe Comment passer d'un objet en un autre en le découpant finement et en recollant les morceaux ? En topologie, traduire objet ou surface par le mot dédié: variété. Changement de forme La chirurgie topologique est une technique fondamentale en topologie différentielle et en géométrie. Elle est utilisée pour modifier les variétés de manière contrôlée. Le but étant de transposer les propriétés d'une variété plus simple à une variété plus compliquée. Historique John Milnor, Michel Kervaire et William Browder ont montré que dans presque toutes les dimensions, toute variété peut être convertie en une sphère exotique par un procédé appelé chirurgie.		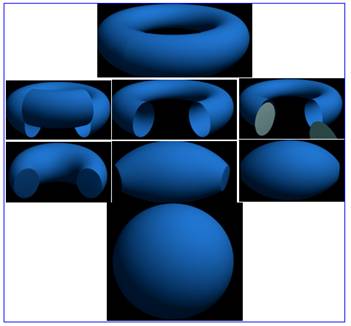Chirurgie du tore transformé en une sphère Lors de cette opération chirurgicale: une partie de la variété est amputée (images 2 et 3); une nouvelle pièce est collée le long de la limite (frontière) de la pièce excisée (image 4: deux disques obturent les ouvertures); et la sphère est obtenue par déformation continue.
Brèves associées	>>> Cobordisme		>>> Brèves Topologie – Index
Pour en savoir plus	>>> Chirurgie topologique		>>> Topologie

1243. Nombre 36
Énigme des trois filles Un dialogue succinct entre deux personnes et l'âge des trois filles peut être déterminé. Énigme résolue du fait de la propriété singulière du nombre 36.		Nombre 36 Deux triplets de nombres (des diviseurs de 36) ont même somme (S) et même produit (P)
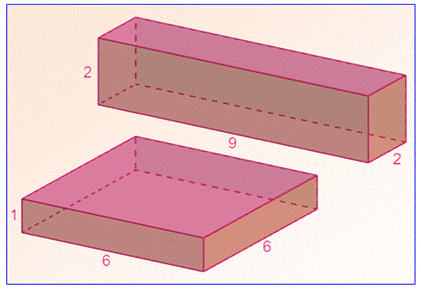
Construction avec ces triplets Deux parallélépipèdes ayant même périmètre* (4 × 13 = 52) et même volume (36) * somme des périmètres des quatre faces (et non longueur des 12 arêtes)
Brèves associées	>>> Nombre 24 en trois chiffres		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Pavé droit et énigme		>>> Énigme des trois filles

1244. Excel: raccourci Somme
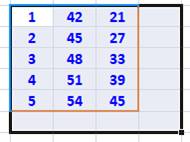
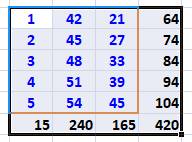
Quelques raccourcis utiles Word et Excel Touche F4 – Répété la dernière action Touche Alt: fait apparaitre les lettres à utiliser pour les raccourcis. Exemple pour accéder à l'insertion de symboles: Word: Alt SY Excel: Alt SS Raccourci somme sur Excel Soit le tableau de nombres indiqué. Souligner les lignes et ou les colonnes où vous désirez avoir les sommes. Appuyer sur Alt et en même temps sur la touche =, toutes les sommes sont calculées.		TOTAUX avec: Sélectionner la zone puis ALT =
Brèves associées	>>> Tableur		>>> Brèves Outils – Index
Pour en savoir plus	>>> Tableur et son utilisation		>>> Outils de programmation

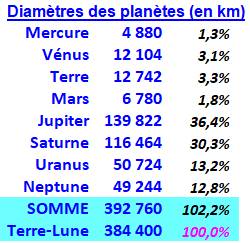
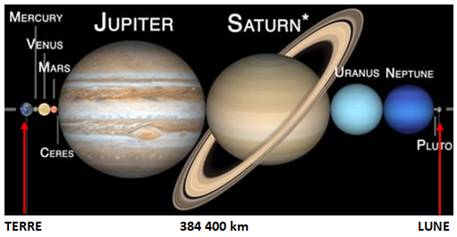
1245. Diamètre des planètes
Brèves associées	>>> Orbites des planètes		>>> Brèves Astronomie – Index
Pour en savoir plus	>>> Planètes du système solaire		>>> Soleil

1246. Anti-diviseurs
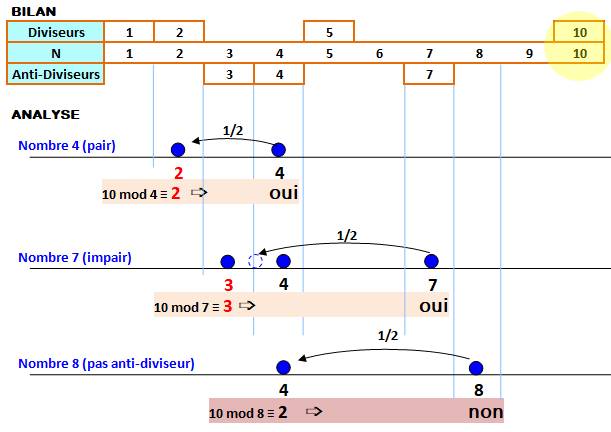
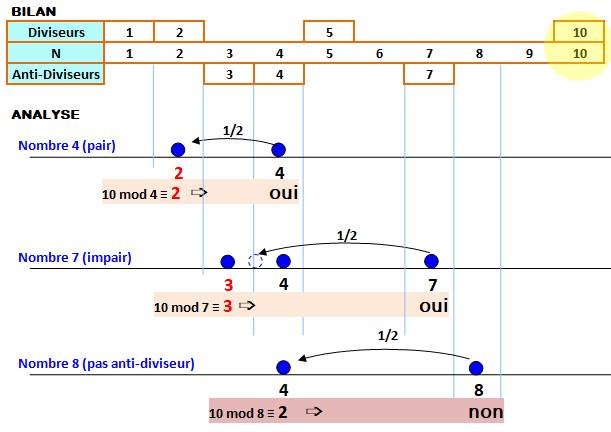
En bref: un nombre k est anti-diviseur de n en cas d'égalité entre: la moitié de k (ou à ½ près si k est impair), et le reste de la division de n par k (exprimé par n mod k). Exemple d'analyse avec le nombre 10: Les nombres {3, 4, 7} sont ses anti-diviseurs. Rappel: 10 mod 4 veut dire reste de la division de 10 par 4
Brèves associées	>>> Diviseurs d'un nombre	>>> Brèves Opérations – Index
Pour en savoir plus	>>> Anti-diviseurs	>>> Diviseurs

1247. Croix de Malte
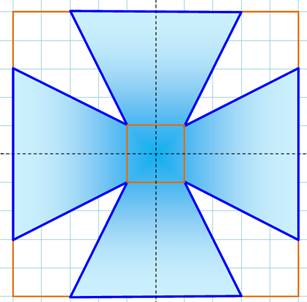
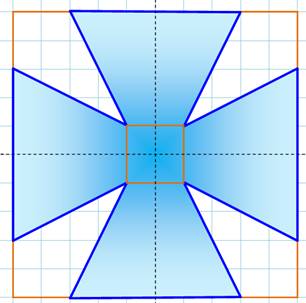
Problème Découper cette croix de Malte en huit morceaux qui, en les assemblant, forment un carré.		Solution Pas évident ! On commence à découper un triangle dans chaque branche. Puis on découpe des pièces en passant par le centre de la croix, et cela pour obtenir les angles droits du carré.
Brèves associées	>>> Pentagone – Dissection		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Solution complète et autre croix		>>> Dissections – Index

1248. Fraction étages pour 100
Comment calculer: 1 / 2 / (3 / 4 / 5 / (6 + 7 + 8 + 9)) Calcul avec présentation linéaire transformée en présentation professionnelle:
Brèves associées	>>> Fraction – Construction géométrique	>>> Brèves Opérations – Index
Pour en savoir plus	>>> Faire 100 avec les chiffres	>>> Faire 100 (suite)

1249. Nombre 97!
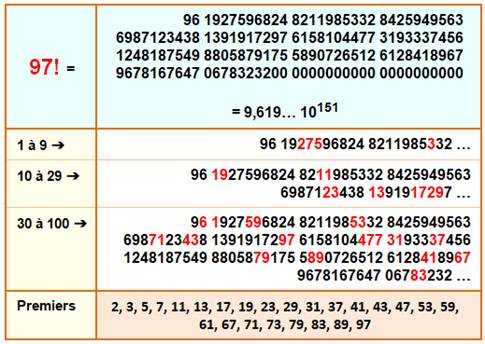
Factorielle 97 Le nombre factoriel 97 = 97! = 1 × 2 × 3 × … × 97 est un grand nombre comportant 152 chiffres. Nombres premiers Ce nombre est sans doute le seul qui contient tous les nombres premiers textuels jusqu'à 97. En rouge dans le tableau, le recensement de tous les nombres premiers de 2 à 97. Ces 25 nombres premiers sont rappelés en dernière ligne.
Brèves associées	>>> Nombre 60		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre 97		>>> Factorielles

1250. Faire n = quatre fois le "k"
Jeu de chiffres Avec principalement les quatre opérations, combiné quatre le nombre k pour obtenir un nombre donné n. Exemples Ci-contre, les cas de quatre 3 et quatre 7 pour obtenir les nombres n de 4 à 10 et quelques autres.
Brèves associées	>>> Quatre 4 – Jeu		>>> Brèves Jeux – Index
Pour en savoir plus	>>> Tableau complet		>>> Jeux de chiffres – Index

1251. Programme Python
Pour se lancer La programmation Python est accessible à tous. Le téléchargement est gratuit. Pour traiter les nombres, il existe des modules complémentaires forts utiles. En raison de sa grande popularité, on trouve de nombreux tutoriels de qualité. Sur mes pages, vous trouverez des exemples et de nombreux trucs à savoir. Programmation Prendre l'habitude de programmer "proprement" vous évitera des ennuis lorsque vos programmes deviendront un peu copieux. La structure donnée en exemple est recommandée, même pour de petits programmes.		Exemple de structure d'un programme Python import math # Fonctions def RC(n): return math.sqrt(n) # Programme principal def main(): n = 121 r = int(RC(121)) print(f"Racine de {n} = {r}") if __name__ == "__main__": main() ð Racine de 121 = 11
Brèves associées	>>> Mon tout premier programme		>>> Brèves Programmes – Index
Pour en savoir plus	>>> Programmer en Python		>>> Python – Index

1252. Énigme 180, 360
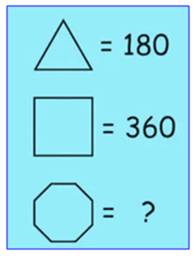
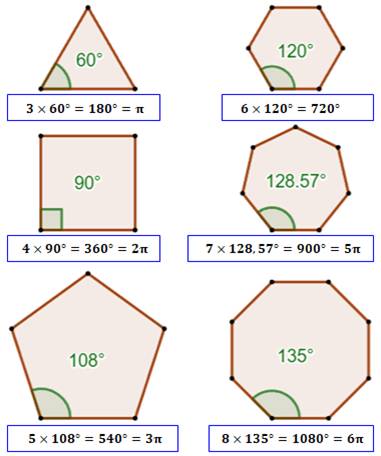
Énigme On demande de préciser la troisième valeur. Solution Il s'agit évidemment de polygones réguliers à 3, 4 et 8 côtés: triangle équilatéral, carré et octogone. On pourrait penser que ces nombres représentent l'aire des formes proposées. Il y a plus simple ! C'est la somme des angles internes aux polygones. Ainsi pour l'octogone, on aura 1080°.		Angles et sommes des angles des polygones Formule générale pour un polygone régulier à n côtes
Brèves associées	>>> Aire mystère du triangle		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Angles des polygones		>>> Énigmes virales Internet

1253. Calcul d'angles
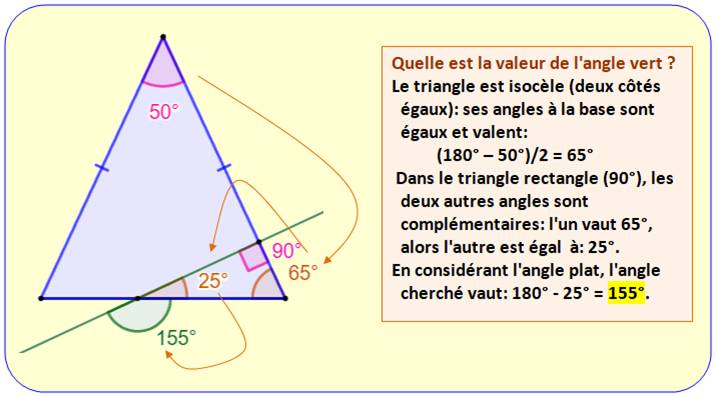
Brèves associées	>>> Angles	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Angles dans le triangle >>> Angles en géométrie	>>> Triangle isocèle

1254. Quatre 3 en fractions
Calculer cette fraction La notation de la fraction proposée est ambigüe. Cependant, on l'interprète comme 3 divisé par le bloc: 3/3/3. Dans ce bloc, les opérations s'effectuent de la gauche vers la droite: soit 1/3. Finalement 3 divisé par 1/3 équivaut à 3 multiplié par 3, soir 3² = 9. Le résultat est général: avec n, on aura un résultat égal à n².
Brèves associées	>>> Fractions avec nombres consécutifs		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Quatre 3 en fractions (suite)		>>> Fractions – Index

1255. Résolution équation en 4^x
Piste: puissance On sait que les puissances d'un produit s'ajoutent: 5^3 × 5^4 = 5^3+4 = 5^7 La réciproque s'applique: 5^7 = 5^2 × 5^5 Dans notre cas: 4^x+2 = 4^x × 4^2 Piste: logarithme Avec une inconnue en puissance, on a recours aux logarithmes
Brèves associées	>>> Équation en x^45 et solution de Viète		>>> Brèves Équations – Index
Pour en savoir plus	>>> Résoudre cette équation (suite)		>>> Défis en algèbre – Index

1256. Calcul d'aire sur l'escalier
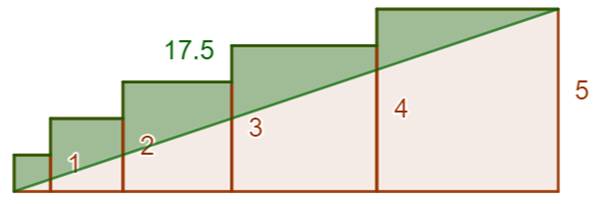
Construction Cinq carrés adjacents de côtés 1, 2, 3, 4 et 5 cm. La diagonale délimite un polygone vert. Quelle est son aire ? Calculs
Brèves associées	>>> Aire du poisson	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Aires des formes classiques	>>> Défis en géométrie – Carrés

1257. Énigme classique – Taille ?
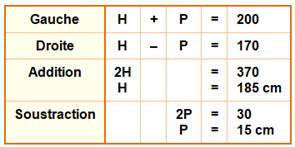
Énigme: taille du perroquet ?		Calcul avec H = Homme et P = Perroquet Solution La taille du perroquet est égale à la moitié de la différence des hauteurs indiquées: P = 15 cm.		Solution visuelle
Brèves associées	>>> Araignée sur une boite		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Énigmes des deux échelles		>>> Jeux et énigmes – Index

1258. Pétales dans hexagone
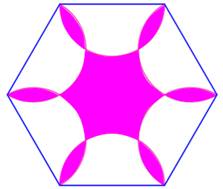
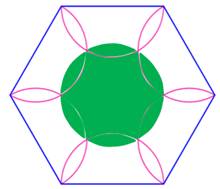
Construction Un hexagone et des demi-cercles construits sur les côtés. Observation Le premier dessin montre une figure rose à pétales. En repliant les pétales, on obtient la figure de droite. Conclusion Aire rose est égale = aire verte = aire du cercle dont le rayon est égal au côté de l'hexagone (cf. figures du bas: tracés verts).
Brèves associées	>>> Hexagone et triangles		>>> Géométrie – Index
Pour en savoir plus	>>> Rosaces		>>> Hexagone

N'oubliez pas d'aller voir la rubrique: Défis en géométrie

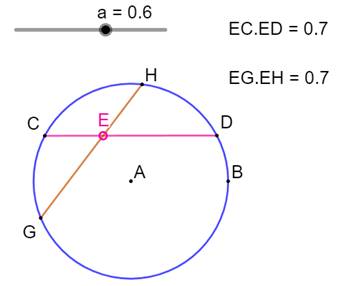
1259. Puissance d'un point
Puissance d'un point La puissance du point E par rapport au cercle est simplement égale au produit des longueurs des cordes EC et ED, par exemple. Théorème La puissance d'un point E par rapport au cercle est constante quelle que soit la corde choisie. En déplaçant le point G sur le cercle, le produit reste égal à 0,7. En modifiant la position du point E (avec le curseur), évidemment la valeur de la puissance est modifiée, mais reste constante. Démonstration Les angles en C et H interceptent un même arc, ils sont égaux. Idem pour les angles en G et D. Les triangles ECD et EDH sont semblables. Proportions: EC / EH = EG / ED Soit les produits: EC∙ ED = EH ∙ EG
Brèves associées	>>> Cercle, carré et cordes		>>> Géométrie – Index
Pour en savoir plus	>>> Théorème des cordes sécantes		>>> Puissance d'un point

Retour	Brèves de maths – Page 62
Suite	Brèves de maths – Page 64
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve63.htm