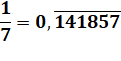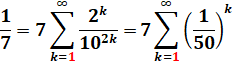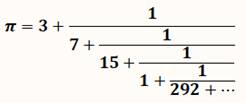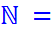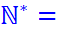NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Page 10 (180-199)		Page 11 (200-219)		Page 12 (220-239)		Page 13 (240-259)		Page 14 (260-279)
	Page 15 (280-299)		Page 16 (300-319)		Page 17 (320-339)		Page 18 (340-359)		Page 19 (360-379)

BRÈVES de MATHS – Page 19

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

360. Multiplication économe
Multiplication inventée pour utilisation avec les ordinateurs. But: réduire les calculs pour réduire le temps d'exécution. Pour multiplier les grands nombres, ceux-ci sont coupés en 2, puis chacun encore en 2, etc. La méthode est économe en puissance de calcul (la multiplication est beaucoup plus exigeante que l'addition). En revanche, elle est gourmande en mémoire.
Brèves Associées	>>> Multiplication rapide à pivot	>>> Multiplications proches de 100
Pour en savoir plus	>>> Multiplications économe des grands nombres	>>> Calcul mental – Index

361. Multiplication paysanne
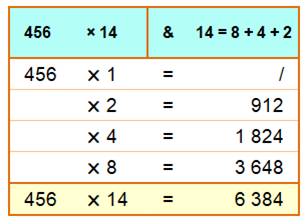
Méthode dite aussi à la russe Méthode connue des Égyptiens et encore utilisée en Russie. Elle offre l'avantage de n'utiliser que la multiplication par 2, qui n'est, en fait, que l'addition du nombre avec lui-même. Algorithme Le multiplicateur est décomposé en une somme de puissances de 2. Le multiplicande est doublé sur chaque ligne. Ne sont retenus pour la somme que les lignes correspondant aux puissances de 2 constituant le multiplicande. Sur l'exemple 456 x 14 = 456 x (8 + 4 + 2) = 456 x 2 + 456 x 4 + 456 x 8		Exemple de disposition Notez que: 14 = 1110 en binaire Ce sont donc les lignes avec un 1 binaire qui sont sommées.
Brèves Associées	>>> Multiplication rapide à pivot		>>> Multiplications proches de 100
Pour en savoir plus	>>> Multiplications paysanne à la russe		>>> Binaire

362. Nombre 1000
Une image vaut mille mots – Confucius Un voyage de mille li a commencé par un premier pas – Lao-Tseu Propriétés Divisible par: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000. Préfixes Mille = 10³ = 1 kilo (k) Un millième = 10^-3 = milli (m) Un polygone à 1000 côtés est un chiliogone Unités 1000 litres = 1 mètre-cube (m³)		Orthographe Trois mille Trois milliers Des mille-pattes Jeu des quatre 4 et jeu de mille en 8 1000 = 888 + 88 + 8 + 8 + 8 Jeu des opérations pannumériques Jeu du diable 1 000 = (6666 – 666) / 6
Brèves associées	>>> Nombre 10 >>> Nombre 100		>>> Orthographe des nombres
Pour en savoir plus	>>> Nombre 1000 dans le DicoNombre		>>> Jeu des quatre 4

363. Hexagone et triangles
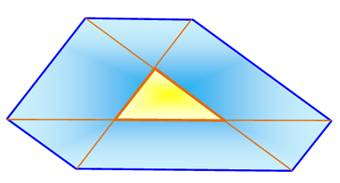
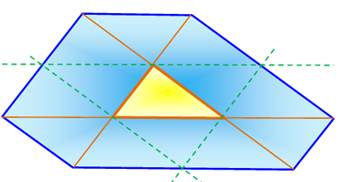
Cet hexagone irrégulier est construit à partir d'un triangle quelconque (jaune). Chaque côté est prolongé de part et d'autre d'une longueur égale précisément à celle du côté prolongé. L'aire de l'hexagone est égale à 13 fois celle du triangle originel: H = 13 t En effet (illustration du bas) Le tracé des parallèles (en vert) *à chaque côté du triangle et passant par le sommet opposé, révèle une figure comportant 12 triangles qui sont égaux au triangle original.** * Aujourd'hui, on dit superposables ou isométriques.
Brèves Associées	>>> Tout triangle est isocèle (?)	>>> Sangakus
Pour en savoir plus	>>> Hexagone	>>> Polygones

364. Divisibilités avec factorielles
Soit la somme des entiers de 1 à n. Quand est-elle divisible par une factorielle ? Exemple 1 1+ 2 + 3 + … + 15 = 120 et 120 = 5 x 4! = 1 x 5! La somme des nombres de 1 à 15 est divisible par le produit des nombres de 1 à 5. Exemple 2 1+ 2 + 3 + … + 224 = 25 200 et 25 200 = 35 x 6! = 5 x 7! La somme des nombres de 1 à 224 est divisible par le produit des nombres de 1 à 7.		Problème équivalent La somme jusqu'à n vaut: S_n = n (n + 1) / 2. Finalement, il s'agit de trouver la plus petite factorielle qui divise le produit de deux nombres consécutifs. Calculs
Brèves Associées	>>> Divisibilité du produit de nombres		>>> Divisibilité de 123456789 – Critères
Pour en savoir plus	>>> Divisibilité par des factorielles >>> Divisibilité – Critères		>>> Somme des entiers >>> Nombre 224

365. Complexité algorithmique

Principe de la notation

Un algorithme peut être simple ou complexe à exécuter. C.a.d. Mobiliser plus ou moins de ressources (calcul et mémoire) pour atteindre le résultat escompté.

Un algorithme qui calcule le carré des nombres de 1 à 100 fait cent passages dans une boucle d'analyse. La fonction qui donne le coût de l'analyse est f(n) = n (une fonction linéaire) et la complexité est notée O(n).

Un algorithme qui calcule la table de multiplication jusqu'à 100 x 100 comporte deux boucles d'analyse, une pour chaque multiplicande. Soit 100² passages dans les boucles. La fonction est f(n) = n² et la complexité est notée O(n²).

Notations

0(…)	complexité	n = 10
1	constante	1
ln(n)	logarithmique	3
n	linéaire	10
n ln(n)	quasi linéaire	33
n²	quadratique	100
n³	cubique	1000
n^k	polynomiale	…
n^ln(n)	quasi polynomiale	2098
2ⁿ	exponentielle	1024
n!	factorielle	3 628 800

Brèves Associées

>>> Algorithmes les plus importants de l'histoire

Pour en savoir plus

>>> Complexité

>>> Algorithmes

>>> Symboles en mathématique

366. Cercles de Ford
Suite fractale de cercles tangents Chaque cercle de Ford est associé à une fraction irréductible en p/q, et, chacun est tangent à une droite horizontale et aux cercles voisins. Centre et rayons des cercles
Brèves Associées	>>> Fractale	>>> Cercles et angles
Pour en savoir plus	>>> Cercle de Ford	>>> Suite de Farey

367. Calcul modulo
Défi Montrer que 5⁶ – 7⁴ est divisible par 3, sans faire le calcul. Préparation du calcul modulo Le reste de la division de 5 par 3 est 2. On écrit en abrégé: Le reste de la division de 7 par 3 est 1 On écrit en abrégé: Le signe égal à trois barres montre qu'il ne s'agit pas d'une vraie égalité, mais d'une égalité entre opérations sur les restes.		Calcul modulo 3 On reprend le nombre à analyser et on remplace par les modulos: Et ce nombre 63 est bien divisible par 3, ce qui veut dire que le nombre initial est aussi divisible par 3. On montre, avec la même méthode que: et donc que ce nombre est toujours divisible par 3. Application En arithmétique, il existe bien des cas où travailler sur le reste des divisions par un nombre donné suffit, sans s'encombrer des quotients.
Brèves Associées	>>> Modulo – Divisibilité par 5 >>> Calcul modulo de 5²¹ – 7¹²		>>> Cinq nombres divisibles par 3
Pour en savoir plus	>>> Calcul modulo (Congruence)		>>> Carte postale 2214

368. Fraction 1/7
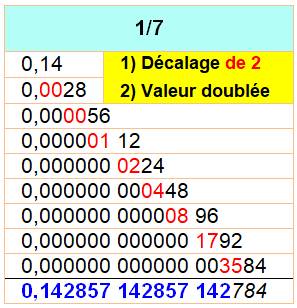
1 / 7 = 0, 142857 142857 … Notation Nombre périodique dont la période est: 142857 <= 14, 28 (multiplication par 2) et 56 + 1 Sommes avec les chiffres 142 + 857 = 999 14 + 28 + 57 = 99 Somme infinie		Formation des chiffres de 1/7
Brèves Associées	>>> Nombre 7		>>> Fraction et série infinie
Pour en savoir plus	>>> Nombre 0,142857 … = 1/7 >>> Nombre de Carroll		>>> Nombres périodiques >>> Fractions et suites de nombres

369. Approximation des irrationnels
Les meilleures approximations d'un nombre irrationnel (nombres à décimales différentes sans fin) sont encapsulées dans sa fraction continue. Chaque développement d'une partie produit une fraction proche du nombre. Fraction continue pour Pi Approximations de Pi (réduites de Pi) – Exemples La première se calcule avec 3 + 1/7 = 22/7.		Théorème de Dirichlet Pour tout nombre irrationnel, il existe une infinité de fractions qui s'approchent du nombre de plus en plus près. L'erreur est inférieure au carré de la fraction "1 / dénominateur". La fraction 22/7 est proche de Pi à moins de 1/7². Pi – 22/7 = 0,0012… et 1/49 = 0,02… Théorème (ex conjecture) de Duffin-Schaeffer Soit un jeu infini de dénominateurs et une tolérance sur l'approximation, ce théorème indique si oui ou non, il est alors possible d'approximer tous les nombres irrationnels. *Démontrée en 2019.*
Brèves Associées	>>> Constante Pi	>>> Nombre d'or
Pour en savoir plus	>>> Fractions continues >>> Réduites de Pi	>>> Théorème de Dirichlet >>> Conjecture de Duffin-Schaeffer

370. Constructions du jardinier
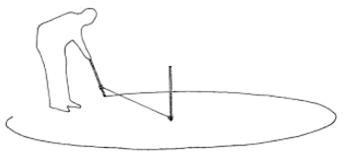
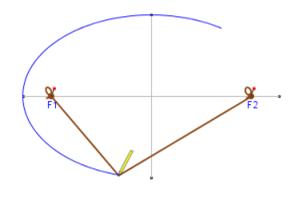
Pour tracer un cercle au sol en ayant accès au centre, il suffit de planter un piquet au centre, de tendre une ficelle de longueur égale au rayon souhaité. Avec un plantoir, un clou ou une craie, marquer le sol en tournant autour du piquet, ficelle bien tendue.
Pour tracer une ellipse au sol en ayant accès aux deux foyers, planter deux piquets aux foyers et tendre une corde fixée à ces deux piquets. Avec un clou ou une craie, tendre la ficelle et marquer le sol en tournant autour des piquets, ficelle bien tendue. Voir Ellipse du jardinier
Brèves Associées	>>> Centre du cercle	>>> Rosace – Hexagone
Pour en savoir plus	>>> Constructions du jardinier	>>> Cercle >>> Ellipse

371. Diagramme de Venn
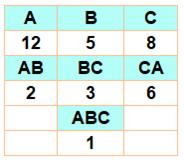
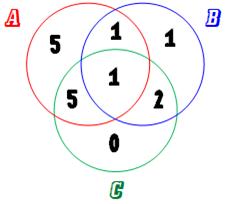
Problème Examen avec trois matières: Algèbre, Biologie et Chimie pour 41 étudiants. Le tableau indique les non-reçus selon la ou les matières: Combien sont-ils à avoir échoué dans une matière au moins ? Commentaires Le diagramme de Venn est ici complètement résolu et il donne bien d'autres renseignements: Avec 41 candidats, si 15 ont échoué quelque part, il y en a 26 qui ont réussi dans les trois matières à la fois. 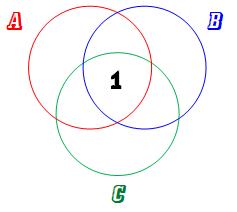Si quelqu'un a échoué en chimie, il a aussi manqué une autre matière (C seul = 0) Il y a 3 personnes qui on réussi l'algèbre sans réussir la chimie et la biologie (zone de B et C sans A => 1 + 2 + 0 = 3)		Résolution en trois temps Trois zones (ici des cercles) représentent les échecs dans chacune des disciplines. De manière évidente, on peut dire que l'intersection ABC contient un individu. 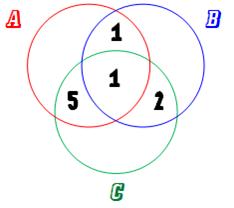Parmi les 2 qui ont échoué en AB, un a aussi échoué en ABC; reste un seul individu qui a échoué en AB seulement. Même raisonnement pour AC en propre: 3 – 1 = 2 et pour BC: 6 – 1 = 5. Parmi les 12 qui ont échoué en A, 5 + 1 + 1 ont aussi échoué ailleurs. Reste: 12 – 7 = 5 qui ont échoué en A seulement. Pour B: 5 – 4 = 1 et pour C: 8 – 8 = 0. Bilan: 5 + 1 + 1 + 1 + 5 + 2 + 0 = 15 personnes ont échoué à au moins une matière (somme des nombres dans les cercles).
Brèves Associées	>>> Tirages de boules		>>> Syllogismes
Pour en savoir plus	>>> Diagramme de Venn		>>> Bases du dénombrement

372. Solstices et équinoxes – Dates
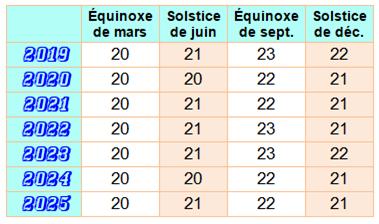
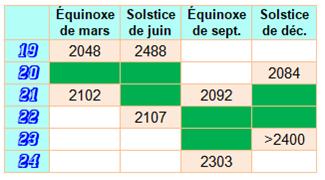
Dates pour 2019 à 2025 Les dates varient selon l'année en tenant compte des années bissextiles. Elles peuvent différer d'un endroit du globe à un autre selon le fuseau horaire.		Amplitude des dates (du 19 au 24 du mois) En vert, les jours les plus probables. En ocre, les jours rares avec l'année de la prochaine apparition. L'équinoxe de septembre ne s'est jamais produit un 21 depuis la mise en place du calendrier grégorien (1582). Le premier tombera en 2092. Le dernier 24 septembre fut en 1931 et le suivant se produira en 2303.
Brèves Associées	>>> L'Univers		>>> Galileo et GPS
Pour en savoir plus	>>> Solstices et équinoxes		>>> Années bissextiles

373. Persistance multiplicative
La persistance multiplicative (PM) est la quantité de fois qu'il faut multiplier les chiffres d'un nombre pour arriver à un chiffre unique. Exemple: PM(77) = 4 Trouver le plus petit représentant pour 423 423 => 4x2x3 = 24 => 2x4 = 8 On peut ordonner les chiffres en croissant. 234 => 2x3x4= 24 => 2x4 = 8 Il y a mieux, en remplaçant 2x3 = 6, on obtient un nombre plus petit (46) ayant la même persistance. Le nombre 46 est donc le représentant de tous ces nombres {46, 64, 234, 243, 324, 342, 423 et 432}.		Plus petit nombre de persistance donnée Le plus petit nombre avec PM = 5, par exemple est 679: 679 => 378 => 168 => 48 => 32 => 6 La plus grande persistance multiplicative connue est 11 et le plus petit nombre de cette catégorie est ce nombre (2,7… 10¹⁴) , suivi des produits successifs: 277 777 788 888 899 On ne connait pas de nombre de persistance égale à 12. S'il existe, il est plus grand que 10²³³. La recherche sera optimisée en se limitant aux représentants de chaque groupe de nombres.
Brèves Associées	>>> Nombre 153 et cycle-cube		>>> Procédé de Kaprekar
Pour en savoir plus	>>> Persistance multiplicative		>>> Nombre 2,7 …10¹⁴

374. Nombres entiers
Nombres entiers naturels, abrégé en naturels. Ce sont les nombres de tous les jours. Ceux qui servent à compter. Sans confusion possible, on dit "entiers" et pour les distinguer des entiers relatifs, on dit "entiers naturels". Ils sont toujours positifs et l'on omet de placer un signe plus devant ces nombres. Notation de l'ensemble des nombres entiers { 0, 1, 2, 3 … } { 1, 2, 3 … }		Théorème fondamental de l'arithmétique Tout nombre entier naturel est décomposable de façon unique en produit de ses diviseurs premiers, sans tenir compte des permutations. Ex: 210 = 2 x 3 x 5 x 7 Équations particulières Les équations diophantiennes sont des équations avec coefficients entiers dont les racines sont des nombres entiers. Ex: x² + y² = 2z² avec x = 1, y = 7 et z = 5
Brèves Associées	>>> Nombres entiers >>> Nombres premiers		>>> Nombres géométriques
Pour en savoir plus	>>> Nombre entiers >>> Type de nombres >>> Équations diophantiennes		>>> DicoNombre: dictionnaires des nombres de 0 à l'infini >>> Théorème fondamental de l'arithmétique

375. Suite trompeuse
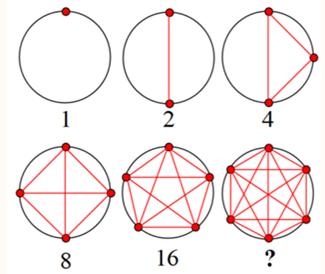
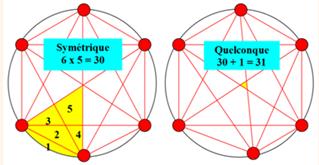
Donnez la suite de cette série de nombres: 1, 2, 4, 8, 16, ? Ce n'est pas toujours 32, une puissance de 2, comme vous allons le voir. Prenez un cercle et inscrire un nombre croissant de points quelconques sur la circonférence. Tirez toutes les cordes possibles. Combien dénombrez-vous de régions ? Cet exemple est souvent utilisé pour montrer qu'il n'est pas toujours judicieux d'extrapoler. On peut avoir des surprises. Dans le cas des cercles, la valeur suivante n'est jamais 32, mais 30 dans le cas d'une disposition régulière ou 31 pour une disposition quelconque.		Régions jusqu'à 5 points Régions avec 6 points réguliers ou quelconques Différence: apparition du petit triangle au centre.
Brèves Associées	>>> Chemin eulérien des nombres		>>> La suite qui se lit
Pour en savoir plus	>>> Régions dans le cercle		>>> Puissance de 2

376. Angle triple
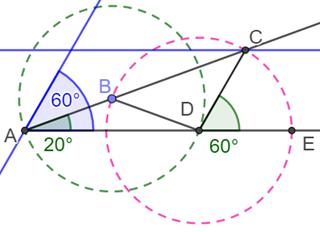
Construction Dessinez l'angle (ici exemple de 20°). Sommet A et un point quelconque B. Cercle de centre B et de rayon AB, coupe l'autre côté de l'angle en D (triangle isocèle ABD). Cercle de centre D et de rayon DB, coupe le premier côté de l'angle en C (triangle isocèle BDC). L'angle CDE est le triple de l'angle BAD. Les deux parallèles dessinées en bleu permettent de ramener l'angle triple sur l'angle initial. Demonstration express angle ABD = 180 – 2a (a = angle BAD) angle CBD = 180 – (180 – 2a) = 2a angle BDC = 180 – 2 × 2a angle CDE = 180 – (180 – 4a) – a = 3a		Exemple avec un angle initial de 20° Les triangles ABD et BDC ont deux côtés de même longueur (rayon des cercles); ils sont isocèles. Les angles à la base sont égaux.
Brèves Associées	>>> Médiatrice – Construction	>>> Rayon du cercle et cordes sécantes
Pour en savoir plus	>>> Angle triple >>> Trisection de l'angle	>>> Somme des angles du triangle >>> Triangle isocèle

377. Suite de Sherlock Holmes
Énigme L'énigme originelle est annoncée par une citation de Conan Doyle où il est question d'un chien qui n'a pas aboyé la nuit; ce qui serait un signe de mystère à éclaircir.		Le mystère: complétez la suite: 1, 2, 4, 7, 8, 11, 14, 16, 17, 19, 22, 26, 28, 29, 41, 44, ?
Solution Parfois il est intéressant d'écrire la suite miroir, celle des nombres manquants. En rose, les multiples de 3, par exemple.		Tous les nombres manquants 3, 5, 6, 9, 10, 12, 13, 15, 18, 20, 21, 23, 24, 25, 27, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 42, 43.
Ce qui reste. En rose les multiples de 5		5, 10, 13, 20, 23, 25, 31, 32, 34, 35, 37, 38, 40, 43.
Bilan La suite proposée est la suite des nombres entiers dont on a retiré: les multiples de 3 et de 5, et les nombres contenant un 3 ou un 5.		1, 2, 4, 7, 8, 11, 14, 16, 17, 19, 22, 26, 28, 29, 41, 44. La suite jusqu'à 100: 46, 47, 49, 61, 62, 64, 67, 68, 71, 74, 76, 77, 79, 82, 86, 88, 89, 91, 92, 94, 97, 98.
Brèves Associées	>>> Nombres 1, 1, 2, 3, 5… – Fibonacci		>>> Fraction et série infinie
Pour en savoir plus	>>> Suite de Sherlock Holmes		>>> Suites

378. Lignes trigonométriques
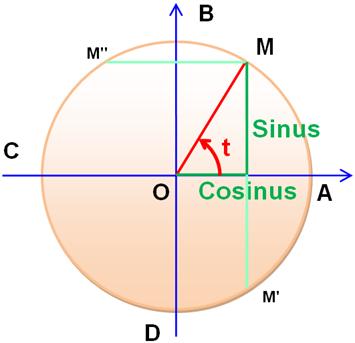
En trigonométrie les coordonnées du point M sur le cercle s'appellent cosinus et sinus. Ce sont des valeurs qui caractérisent aussi l'angle t. Elles prennent des valeurs exclusivement entre -1 et +1. Une valeur de cosinus caractérise deux points sur le cercle: M et M'. Une valeur de sinus caractérise deux points sur le cercle: M et M". Le COsinus est à CÔté de l'angle. Le sinus est si loin …
Brèves associées	>>> Mesurer les angles	>>> Valeurs trigonométriques
Pour en savoir plus	>>> Lignes trigonométriques	>>> Trigonométrie >>> Terrain de jeu de la trigonométrie

379. Nombre 1001
1 001 = 7 x 11 x 13, un nombre sphénique avec trois facteurs premiers consécutifs. Le plus petit nombre palindrome à quatre chiffres. Conte des mille et une nuits avec Shéhérazade. Il ya mille et une façon de faire.		Combinaisons Il y a mille et une façons de prendre 4 boules dans un panier de 14 boules (combinaisons). Ce nombre appartient donc au triangle de Pascal.
Brèves Associées	>>> Nombre 100		>>> Nombre 2019
Pour en savoir plus	>>> Nombre 1 001 >>> Nombres 1000 et suite		>>> Triangle de Pascal >>> Combinaisons >>> Expressions avec mille et un

Retour	Brèves de maths – Page 18
Suite	Brèves de maths – Page 20
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve19.htm

360. Multiplication économe

361. Multiplication paysanne

362. Nombre 1000

363. Hexagone et triangles

364. Divisibilités avec factorielles

365. Complexité algorithmique

366. Cercles de Ford

367. Calcul modulo

368. Fraction 1/7

369. Approximation des irrationnels

370. Constructions du jardinier

371. Diagramme de Venn

372. Solstices et équinoxes – Dates

373. Persistance multiplicative

374. Nombres entiers

375. Suite trompeuse

376. Angle triple

377. Suite de Sherlock Holmes

378. Lignes trigonométriques

379. Nombre 1001