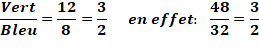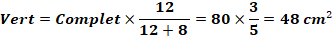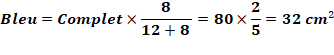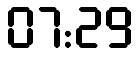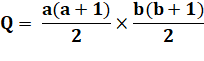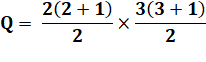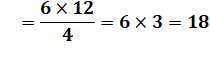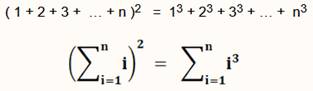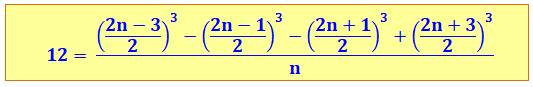NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/03/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 20		Page 40		Page 50		Page 60			Page 70
	Page 60 (1180-1199)		Page 61 (1200-1219)		Page 62 (1220-1239)		Page 63 (1340-1459)		Page 64 (1360-1479)
	Page 65 (1380-1499)		Page 66 (1400-1419)		Page 67 (1420-1439)		Page 68 (1440-1469)		Page 69 (1460-1479)

BRÈVES de MATHS – Page 61

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

1200. Programme Langlands
Approche Le Programme de Langlands est le plus important des concepts mathématiques des dernières décennies. Inutile de dire que ce concept est hors de portée de la majorité d'entre nous, sauf à être titulaire d'un bon bagage supérieur en mathématiques. Unification mathématique Le Programme de Langlands conjecture l'existence de liens très profonds entre plusieurs domaines fondamentaux des mathématiques, notamment: L'algèbre et l'arithmétique (et plus généralement la théorie des nombres) via notamment les travaux sur la théorie de la résolution des équations algébriques prenant naissance dans les travaux sur les groupes de Galois. L'analyse harmonique qui consiste à s'intéresser aux phénomènes ondulatoires (ondes lumineuses, gravitationnelles, ou sonores) en les "dépliant" dans le domaine fréquentiel grâce aux séries ou transformées de Fourier. La géométrie qui, notamment, identifie la symétrie caractérisant un objet dont les propriétés sont conservées suite à un mouvement dans l'espace ou dans le temps.		À la recherche de l'unification des domaines mathématiques
Brèves associées	>>> Calcul différentiel et intégral	>>> Brèves Maths – Index
Pour en savoir plus	>>> Programme de Langlands >>> Conjecture de Brauer	>>> Transformée de Fourier >>> Structures algébriques

Culture au fil de l'eau

Carnaval: vient du latin: carne, viande et levare, enlever, via l'italien carnevale. La fin du carnaval est le mardi gras), suit le mercredi des cendres qui marque le début du carême. >>>

1201. Principe du transistor
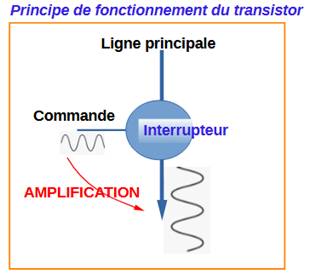
Approche Comment démystifier le transistor ? Les transistors jouent un rôle essentiel dans tous les appareils électroniques: des téléviseurs aux ordinateurs en passant par les machines à laver. Les transistors sont des composants électroniques à base de semi-conducteurs. Ils servent à la fois d'amplificateur et de commutateur. Principe d'amplification (radio, télévision …) Un transistor peut être comparé à robinet: Un petit tour de robinet (une petite augmentation de tension entre la base et l'émetteur) crée un débit important (une forte tension entre le collecteur et l'émetteur). Un petit signal fluctuant devient un plus grand signal fluctuant identique en forme. Principe de commutation (informatique) Dans ce cas, le transistor agit comme un interrupteur pour le courant électrique. Il ne passe pas (0) ou il passe (1). Des assemblages de transistors composent des nombres binaires, lesquels sont représentatifs de nombres décimaux ou de lettres formant des textes. Cette fonction du transistor se retrouve: dans les mémoires dans les circuits logiques (portes ET, OU, NON).		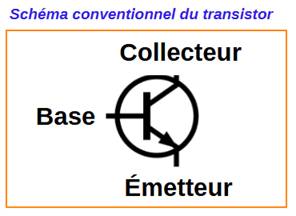Composition Base: elle fonctionne comme une vanne qui contrôle le passage du courant entre collecteur et émetteur. Collecteur: point d'entrée du courant à réguler. Émetteur: point de sortie.
Brèves associées	>>> Microprocesseur		>>> Brèves Électronique – Index
Pour en savoir plus	>>> Composants électroniques – Index >>> Informatique – Index		>>> Circuits logiques >>> Puces de microprocesseurs >>> Numération binaire

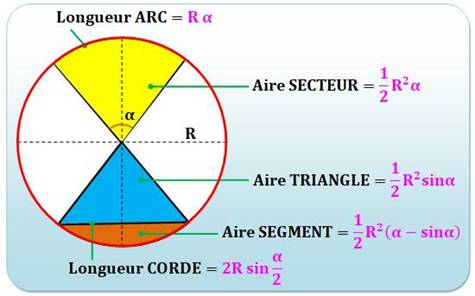
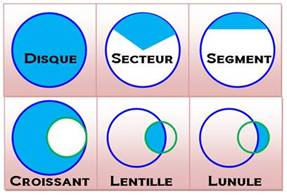
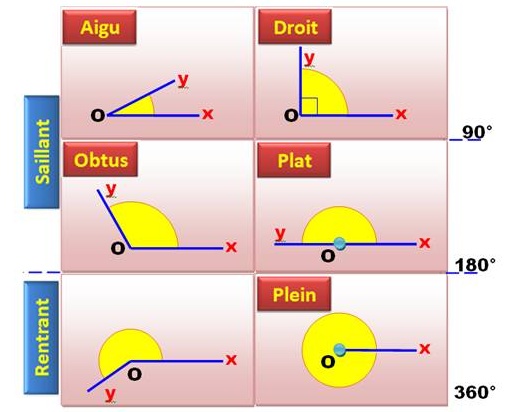
1202. Éléments du cercle
Brèves associées	>>> Cercle – Formulaire		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Éléments du cercle		>>> Cercle – Index

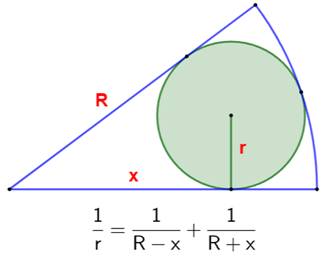
1203. Cercle dans secteur
Construction Un secteur de rayon R et d'angle quelconque. Le cercle inscrit dans ce secteur; son rayon est r. La distance du sommet du secteur au point de tangence est noté x. Démontrer la relation indiquée entre R, r et x. Piste Une relation évidente est établie dans un triangle rectangle avec le théorème de Pythagore. La suite est pure affaire de calcul.
Brèves associées	>>> Segment – Aire inter-segments		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Cercle dans l secteur		>>> Aire du secteur

Culture au fil de l'eau

L’Institut Polytechnique de Paris (IP Paris) regroupe six des plus prestigieuses écoles d’ingénieurs:

École polytechnique,

Ensta (École nationale supérieure des techniques avancées),

École nationale des ponts et chaussées,

Ensae (École nationale de la statistique et de l'administration économique),

Télécom Paris de l'Institut Mines-Télécom et

Télécom SudParis de l'Institut Mines-Télécom.

>>>

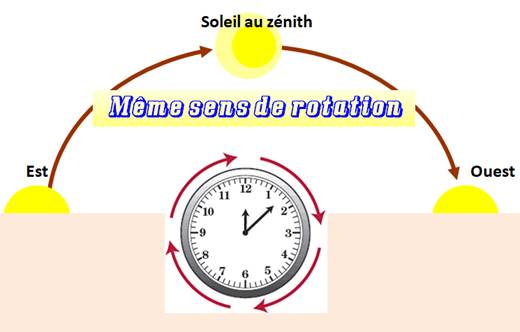
1204. Sens horaire
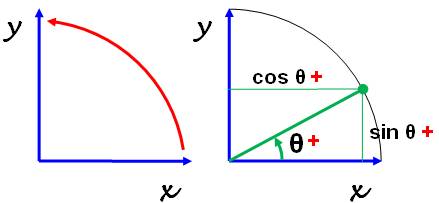
Horloge Les premières horloges furent inventées dans l'hémisphère nord. Le soleil s'y déplace d'est en ouest. Sur un cadran solaire, l'ombre du style se déplace dans le même sens que le Soleil. Le sens des aiguilles de l'horloge a donc été choisi par mimétisme avec celui du trajet du Soleil. Maths Les mathématiciens disent que le sens horaire est le sens négatif de rotation. Le sens positif étant le sens antihoraire. La raison: la rotation simple qui fait passer des abscisses (axe des x) aux ordonnées (axe des y) est la rotation antihoraire. De plus, un angle orienté, compté à partir de l'axe x, produit un sinus et un cosinus positif si l'angle est orienté en antihoraire.
Brèves associées	>>> Orbites des planètes		>>> Brèves Astronomie – Index
Pour en savoir plus	>>> Horloge		>>> Temps – Index

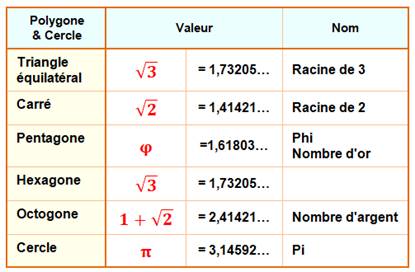
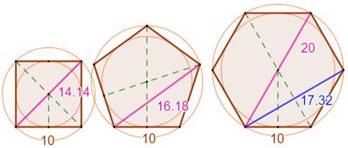
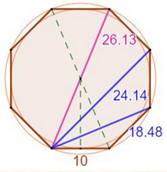
1205. Nombres de la géométrie
Valeurs des nombres emblématiques des polygones et du cercle		Illustrations: longueurs des diagonales
Brèves associées	>>> Nombre d'or et Théorème de Ptolémée		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Longueur des diagonales des polygones		>>> Polygones

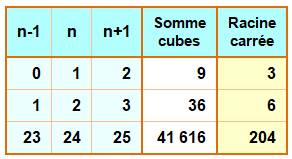
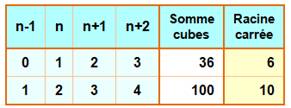
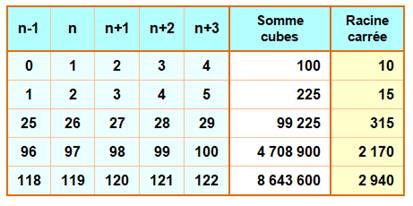
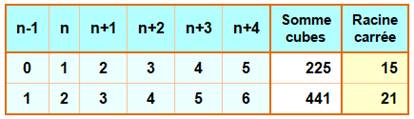
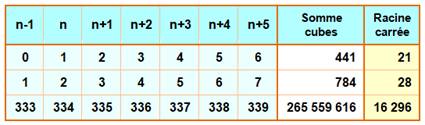
1206. Carré somme de cubes
Approche avec trois termes Somme des cubes de trois nombres consécutifs Quelles sont les valeurs de n pour que E soit un carré ? Et avec plus de cubes ? Seuls cas à trois termes pour n < 10^6 Seuls cas à quatre termes pour n < 10^6		Seuls cas à cinq termes (démontré) Seuls cas à six termes pour n < 10^6 Seuls cas à sept termes pour n < 10^6
Brèves associées	>>> Carré somme de cubes		>>> Brèves Identités – Index
Pour en savoir plus	>>> Carrés somme de cubes >>> Somme de cubes		>>> Nombre 204 >>> Nombre 315

Culture au fil de l'eau

Polymathe: personne d'esprit universel; connaissances dans tous les domaines sciences comme arts.

Henri Poincaré (1854-1912) est l'un des derniers polymathes.

Du grec polus, beaucoup et manthano, savoir.

Polymath est aussi un projet de collaboration en ligne pour résoudre des problèmes de mathématiques.

>>>

1207. Forme polygonale
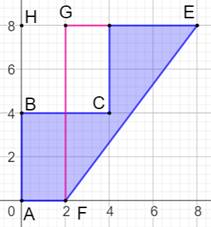
Construction Une forme polygonale. Les longueurs des segments horizontaux et verticaux sont connues. Voir la figure. Quelle est la longueur du segment oblique? Aire de la surface bleue ? Segment oblique Les deux segments verticaux sont translatés sur le segment rose: Longueur 8 cm. Dans le triangle rectangle EFG, les côtés mesurent 8 cm et 6 cm. Avec le théorème de Pythagore: EF² = 8² +6² = 100 = 10² => EF = 10 cm Aire du polygone bleu A = Aire(AFEH) – Aire(BCGH) Aire du trapèze AFEH: ½ (AF + HE) × FG = ½ 10 × 8 = 40 Aire du carré: 4 × 4 = 16 A = 40 – 16 = 24 cm²		Figure initiale Calcul de la longueur du segment oblique
Brèves associées	>>> Polygones et leurs diagonales		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de Pythagore		>>> Trapèze >>> Carré

1208. Aires dans le triangle
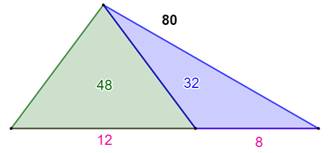
Propriété: proportionnalité Un segment, dit cévienne, découpe le triangle quelconque en deux triangles: vert et bleu. Les aires de ces triangles sont proportionnelles aux longueurs des segments découpés sur le côté du triangle. Aires des deux triangles Connaissant l'aire du triangle complet et les longueurs découpées, on calcule l'aire du triangle vert et celle du triangle bleu:		Proportions pour toute cévienne dans un triangle quelconque (exemple numérique)
Brèves associées	>>> Aires – Comparaison – Triangles		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Aire du triangle		>>> Céviennes

1209. Révision niveau sixième
Droites Segments
Angles
Brèves associées	>>> Les filles et les maths		>>> Brèves – Enseignement – Index
Pour en savoir plus	>>> Révision de sixième		>>> Enseignement – Index

1210. Heures carrées
Affichage des heures sur un réveil numérique Les heures et minutes sont concaténées pour former un nombre de quatre chiffres. Quelles sont les heures et minutes "carrées" ? Exemple de 2025 = 25² => Liste des 34 heures et minutes qui peuvent se lire comme un nombre au carré. En rouge, les cas où le nombre est une puissance quatrième, comme 2401 = 7^4. En jaune, la somme des chiffres est également un carré, comme 2025 => 2 + 0 + 2 + 5 = 9 = 3². Pas d'heure carrée pour les 13h et les 17h.		Seule heure cube: 7 29 = 9^3.
Brèves associées	>>> Calendrier année 2025		>>> Brèves Histoire – Index
Pour en savoir plus	>>> Nombre 2025 = 25²		>>> Temps – Index

1211. Somme de consécutifs
Approche Tous les nombres sont au moins une fois somme de nombres consécutifs, sauf les puissances de 2. On dit qu'ils sont polis. S'il existe k >1 possibilités de sommes de consécutifs, le nombre est k-poli. Exemple: le nombre 15 est 3-poli 15 = 1 + 2 + 3 + 4 + 5 = 4 + 5 + 6 = 7 + 8		Grands polis Parmi les grands polis, le nombre 2025 est 14-poli. Il est par exemple la somme des nombres de 11 à 64, soit 54 termes. Records Les nombres qui sont de plus en plus k-polis sont: 1, 3, 9, 15, 45, 105, 225, 315, 945, 1575, 2835, 3465, 10395, 17325, … Il se trouve que ce sont aussi les nombres impairs hautement composés record.
Brèves associées	>>> Nombres polis ou en escaliers		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Nombres polis ou nombre escaliers >>> Nombres hautement composés		>>> Le nombre 2025 est exceptionnel >>> Nombre 2025 en bref

1212. Rectangles dans une grille
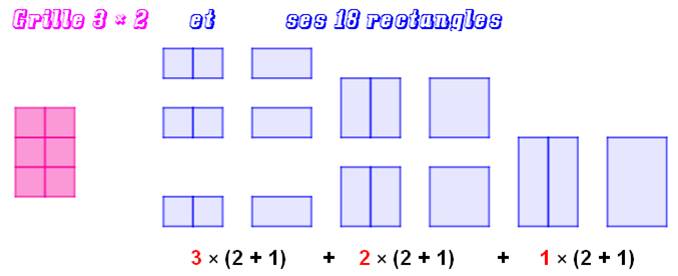
Dénombrement On nous montre une figure formée de 3 traits verticaux et quatre traits horizontaux. Autrement-dit: une grille rectangulaire 3 × 2. Compter les rectangles dans cette grille. Décompte sur la figure Décompte sur une bande horizontale, des rectangles les plus petits au plus grands: 2 + 1 = 3 Décompte selon la largeur de bande en vertical: (3 + 2 + 1) × 3 = 18		Formule générale pour une grille a × b Sur la figure avec cette formule:
Illustration: grille de départ à gauche et sa décomposition en rectangles bleus
Brèves associées	>>> Rectangles dans une grille carrée		>>> Brèves Dénombrement – Index
Pour en savoir plus	>>> Rectangles dans une grille rectangulaire		>>> Nombre 2025

1213. Cubes et impairs
Propriété Conséquence du théorème de Nicomaque: n^3 = (n² – n + 1) + (n² – n + 3) + … + (n² + n – 1) Une somme de nombres impairs consécutifs. Rappel On se souvient que le théorème de Nicomaque dit que la somme des cubes de 1 à n est égale au carré de la somme des nombres de 1 à n:
Brèves associées	>>> Somme des entiers – 2025		>>> Brèves Arithmétique – Index
Pour en savoir plus	>>> Théorème de Nicomaque		>>> Somme des impairs consécutifs

1214. Cinq avancées mathématiques
Contexte Quels sont les cinq avancées mathématiques qui ont changé le cours de l'histoire ? Celles qui ont eu un impact profond. Voici une sélection. Théorème de Pythagore Ce théorème, attribué au philosophe grec ancien Pythagore, fournit une relation fondamentale en géométrie euclidienne entre les trois côtés d'un triangle rectangle. Plus précisément, il indique que le carré de l'hypoténuse (le côté opposé à l'angle droit) est égal à la somme des carrés des deux autres côtés. Il a jeté les bases de l'architecture, de l'ingénierie et de la physique modernes. Il est essentiel dans de nombreux domaines, de la construction de bâtiments à la navigation efficace dans le monde. Au-delà de ses applications pratiques, le théorème a également joué un rôle crucial dans le développement des preuves mathématiques, renforçant l'importance du raisonnement logique. >>> Les Éléments d'Euclide Ouvrage écrit vers 300 avant notre ère, les "Éléments" d'Euclide sont une compilation exhaustive de connaissances couvrant des sujets tels que la géométrie plane, la théorie des nombres et la géométrie tridimensionnelle. Ils ont établi une norme pour la rigueur mathématique et le raisonnement déductif. Ce qui a rendu ce travail révolutionnaire, c'est son approche systématique pour prouver les vérités mathématiques. En commençant par un ensemble d'axiomes et en s'appuyant sur eux, Euclide a démontré comment des théorèmes complexes pouvaient en être logiquement dérivés. Son travail a fourni un plan pour les futurs mathématiciens et a établi un cadre solide pour notre compréhension moderne de la géométrie et des mathématiques dans son ensemble.>>> Analyse: calcul différentiel et intégral Développé simultanément par Isaac Newton et Gottfried Wilhelm Leibniz à la fin du XVIIe siècle, l'analyse (calculus en anglais) fournit les outils pour comprendre le changement, pour modéliser les phénomènes dynamiques comme le mouvement des objets ou comme les phénomènes évolutifs. Il est central dans des domaines tels que la physique, l'ingénierie, l'économie et la biologie, permettant aux scientifiques et aux mathématiciens de modéliser et de prédire avec précision les phénomènes naturels. Dans l'ensemble, le calcul a ouvert la voie à d'innombrables innovations et demeure une pierre angulaire de la science et de la technologie modernes >>> Logarithmes Les logarithmes, et leurs inverses les fonctions exponentielles, ont considérablement accéléré les calculs en physique, en astronomie et en ingénierie. Ils transforment la multiplication en addition, rendant les calculs complexes plus gérables. >>> Loi de la Gravitation La loi de la gravitation de Newton décrit la force de gravitation entre deux objets. Elle explique le mouvement des planètes et a une nature universelle, applicable partout dans l'univers. >>> Conclusion Ces problèmes mathématiques ont non seulement fait progresser le domaine des mathématiques mais ont également profondément influencé la science, la technologie et la vie quotidienne. >>> BONUS: deux autres candidats à ce top 5 Théorème de Fermat-Wiles Le dernier théorème de Fermat est une énigme qui a intrigué les mathématiciens pendant plus de 350 ans. Proposée par Pierre de Fermat en 1637, il affirme qu'il n'y a pas de solution de nombre entier à l'équation x^n + y^n = z^n pour n supérieur à 2. Le théorème n'a été prouvé qu'en 1994 par le mathématicien britannique Andrew Wiles. La poursuite de cette preuve a inspiré des générations de mathématiciens à développer de nouveaux domaines mathématiques, y compris la géométrie algébrique et la théorie des nombres. La résolution du théorème par Wiles était une réalisation monumentale, soulignant la persévérance, la créativité et l'effort de collaboration intrinsèques à la recherche mathématique. Il a également démontré le pouvoir des mathématiques à résoudre les mystères de longue date. >>> Les sept ponts de Koenigsberg: la naissance de la théorie des graphes Le problème des sept ponts de Koenigsberg, posé par Leonhard Euler en 1736, demandait s'il était possible de traverser les sept ponts de la ville sans en traverser plus d'une fois. La solution négative d'Euler à ce problème a jeté les bases de la théorie des graphes. Cette nouvelle branche des mathématiques est devenue essentielle en informatique, car elle fournit le cadre pour l'analyse des réseaux, l'optimisation des itinéraires et la conception de circuits. La théorie des graphes sous-tend la fonctionnalité de l'internet, des moteurs de recherche et des plateformes de médias sociaux, mettant en valeur son impact significatif sur le monde numérique. >>>
Brèves associées	>>> Calendrier 2025	>>> Brèves Histoire – Index
Pour en savoir plus	>>> Les 24 problèmes de Hilbert	>>> Les 7 problèmes de Clay

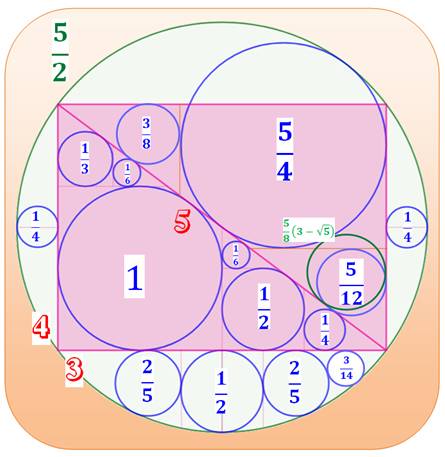
1215. Triangle 345 et ses cercles
Construction Deux triangles rectangles de côtés 3, 4 et 5 sont placés tête-bêche pour former un rectangle (rose). On construit tous les cercles montrés sur la figure et on calcule le rayon de chacun. Calcul du rayon Il s'agit principalement de cercles inscrits dans des triangles rectangles. Si les côtés du triangle rectangle mesurent a et b et si l'hypoténuse mesure c (longueur déduite des deux autres par application du théorème de Pythagore), Alors le rayon du cercle inscrit vaut:		Le rayon du cercle inscrit dans le triangle vaut 1. Les rayons des autres cercles sont des fractions.
Brèves associées	>>> Triangle (a, 60°, b) – Calcul de l'aire		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangle 345 et ses cercles		>>> Triangle 345

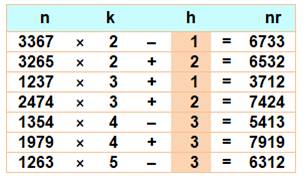
1216. Lien entre nombre et retourné
Retourné Un nombre est le retourné d'un autre lorsqu'on écrit ses chiffres dans l'ordre inverse. Ainsi 123 est retourné en 321. Certains nombres comme 41 et 742 partagent la propriété d'être en relation linéaire simple avec leur retourné. Ces deux nombres sont les seuls pour la relation R(n) = n ∙ k ± 1 avec k > 2. En revanche, ils sont très nombreux (infinité) avec R(n) = n ∙ k ± h avec k > 1 et h >1. Exemples: 73 = 37 × 2 – 1 ; 201 = 102 × 2 – 3 ; 531 = 135 × 4 – 9. Retourné par 2 Un nombre est le retourné par 2 lorsque ses blocs de deux chiffres sont écrits dans l'ordre inverse. Ainsi 12 34 devient 34 12.		Retournés simples en relation linéaire Retournés par 2 en relation linéaire
Brèves associées	>>> Nombres polis ou en escaliers		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Retournés(n) = kn ± h		>>> Nombres retournés

1217. Belles identités avec 5
Identités Avec la puissance cinquième de nombres successifs et deux puissances de 5. Toutes sont en unités 1, 2, 3 et 4. Seule la première est en puissance de 5 successives.
Référence:: Geoffrrey Campbell et Laleksander Zujev – On integer solutions to Les auteurs présentent la théorie et douze solutions dans cette publication par Academia
Brèves associées	>>> Puissance 5 – Unités		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Nombre 750 >>> nombre 78 750		>>> Puissances de 5 >>> Pépites numériques

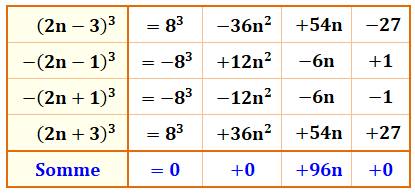
1218. Somme de fractions = 12n
Somme mystérieuse Somme algébrique du cube de fractions en progression arithmétique; en fait, ce sont les quatre nombres impairs 3, 5, 7 et 9 divisés par 2. Cette somme représente le carré de 6; mieux, il est possible sur le même modèle de représenter toutes les puissances de 6. Explication En écrivant la somme sous une forme générique (un nombre impair est noté: 2n + 1), le mystère s'éclaircit. Cette somme vaut toujours 12n. Il suffit d'adapter n pour obtenir des multiples de 12 et, bien sûr, des puissances de 6. Calculs Note En divisant l'expression par n, le résultat est toujours 12 quelle que soit la valeur de n. Cube ou autre puissance ? La même expression, mais avec les puissances 1, 2, 3, 4 et 5, une fois simplifiée, produit les résultats indiqués dans ce tableau:
Brèves associées	>>> Somme et produit	>>> Brèves Motifs – Index
Pour en savoir plus	>>> Identités remarquables	>>> Nombre 12

1219. Calcul rapide des cubes
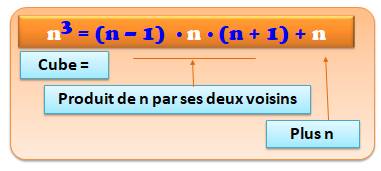
Méthode Pour calculer le cube du nombre n: multiplier n par ses deux voisins, et ajouter n. Justification Soit n et ses deux voisins (n – 1) et (n + 1). Le produit: (n – 1) n (n + 1) = (n – 1) (n² + n) = n^3 + n² – n² – n = n^3 – n En isolant le cube: n^3 = (n – 1) n (n + 1) + n		En bref: Exemples de calculs 3^3 = 2 × 3 × 4 + 3 = 24 + 3 = 27 5^3 = 4 × 5 × 6 + 5 = 120 + 5 = 125 9^3 = 8 × 9 × 10 + 9 = 720 + 9 = 729 11^3 = 10 × 11 × 12 + 11 = 10 × 132 + 11 = 1331 21^3 = 20 × 21 × 22 + 21 = 20 × 462 + 21 = 9240 + 21 = 9261
Brèves associées	>>> Calcul mental de puissances		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Nombres cubes >>> Calcul mental des cubes		>>> Calcul mental – Index

La page précédente est dédiée aux propriétés du nombre extraordinaire: 2025

Retour	Brèves de maths – Page 60
Suite	Brèves de maths – Page 62
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve61.htm