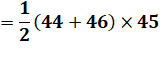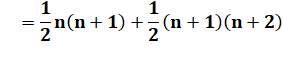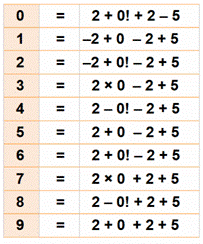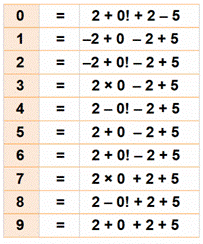NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/05/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 20		Page 40		Page 50		Page 60			Page 70
	Page 60 (1180-1199)		Page 61 (1200-1219)		Page 62 (1220-1239)		Page 63 (1240-1259)		Page 64 (1260-1279)
	Page 65 (1280-1299)		Page 66 (1300-1319)		Page 67 (1320-1339)		Page 68 (1340-1359)		Page 69 (1360-1379)

BRÈVES de MATHS – Page 60

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

Page spéciale consacrée au nombre

Sur cette page, vingt propriétés du nombre 2025 sous forme de brèves.

Et, détails sur le nombre exceptionnel 2025 en DicoNombre 2025 en onze pages

1180. Le nombre 2025 est un carré
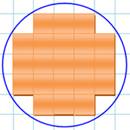
Représentation de 2025 en un carré de 25 unités de côté Notez que la somme de ses chiffres est également un carré: 2 + 0 + 2 + 5 = 9 = 3² Prochaine occurrence avec ces deux propriétés avec 2 304 = 48² et la précédente avec 1681 = 41². SUITE 2025 >>>
Brèves associées	>>> Carré = Somme de cubes	>>> Puissances – Index
Pour en savoir plus	>>> Propriété des carrés	>>> Carré – Index

1181. Année 2025 – Année carrée
Calendrier Année qui commence par un mercredi. C'est la 2025^e année de notre ère, la 25^e année du III^e millénaire et du XXI^e siècle et la 6^e année de la décennie 2020-2029. Du 8 au 17 mars: Jeux Olympiques d'hiver à Turin. L’Organisation des Nations Unies (ONU) a officiellement déclaré 2025 Année internationale de la science et de la technologie quantiques (IYQ2025), coïncidant avec le 100^e anniversaire de la mécanique quantique. Du 10 au 19 mars 2025: La semaine des mathématiques organisée par le ministère de l’Éducation nationale. 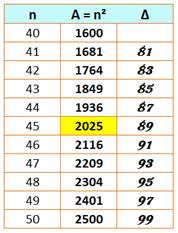SUITE 2025 >>>		Année carrée Première année carrée (2025 = 45²) depuis 1936 (= 44²). Une particularité numérique plutôt rare. Savez-vous que les personnes nées en 1980 ont 45 ans en 2025 = 45² ? Tableau: les précédentes années carrées et les suivantes. Notez l'écart entre elles, proche du siècle. L'écart vaut exactement: 2n – 1.
Brèves associées	>>> Actualités 2018		>>> Histoire – Index
Pour en savoir plus	>>> Année		>>> Calendrier

1182. Nombre composé
Un nombre est premier ou composé. Il est premier si aucun nombre ne peut le diviser; Il est composé s'il existe des nombres qui le divisent. Le nombre 2025 est visiblement divisible par 5, il est composé. Le théorème fondamental de l'arithmétique affirme que: tout nombre est le produit de nombres premiers et que ce produit est unique (sauf à inverser les nombres).			= 3 × 3 × 3 × 3 × 5 × 5 = 81 × 25 Les nombres 3 et 5 sont les facteurs (ou diviseurs premiers) du nombre composé 2025.
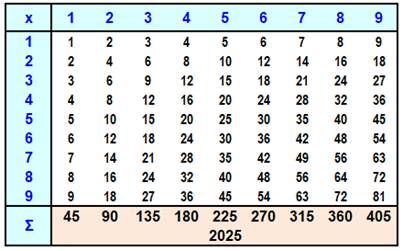
Table de multiplication Avez-vous déjà eu la curiosité d'ajouter tous les nombres de la table de multiplication ? Somme des nombres de la table des multiplications de 1 à 9 = 2 025 SUITE 2025 >>>
Brèves associées	>>> Composés – Record de suite	>>> Types de nombres – Index
Pour en savoir plus	>>> Nombres composés	>>> Premiers et composés – Index

1183. Notation en binaire
Tout nombre est une somme de puissances de 2. La suite de ces puissances est symbolisée par une suite de "1" et de "0". C'est de cette façon que les ordinateurs "voient" ce nombre. Dans une mémoire informatique, il est conservé sous la forme de transistors dont la notation binaire "1" indique ceux qui sont actifs alors que les autres seront au repos.			111 1110 1001 Binaire SUITE 2025 >>>
Brèves associées	>>> Binaire: nombres 0 et 1 >>> Binaire – Conversion	>>> Numération – Index
Pour en savoir plus	>>> Numération binaire	>>> Binaire et informatique

1184. Chiffres Romains
Les notations romaines sont encore utilisées pour indiquer les siècles ou les numéros de rois. Avec 2025 = 2×100 + 2×10 + 5 Soit: MM XX V			MM XX V Romain SUITE 2025 >>>
Brèves associées	>>> Chiffres romains	>>> Numération – Index
Pour en savoir plus	>>> Chiffres romains	>>> Compter comme les Romains

1185. Somme des entiers
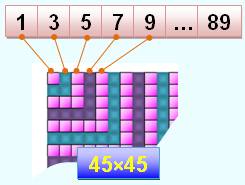
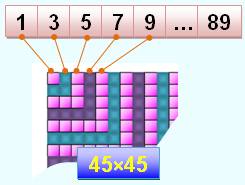
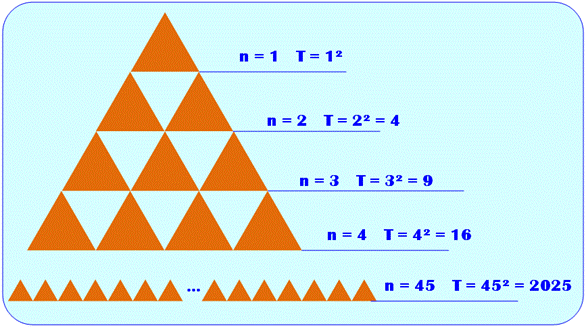
Somme des entiers au carré La somme des nombres de 1 à 9 vaut 45, et 45 x 45 = 2025. La pyramide de la figure symbolise la somme des nombres de 1 à 9 et la parenthèse indique que le total est à mettre au carré. Cela donne : (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) × (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 2025. SUITE 2025 >>>
Brèves associées	>>> Somme des carrés		>>> Arithmétique – Index
Pour en savoir plus	>>> Somme des entiers		>>> Sommes – Index

1186. Somme des cubes
Le nombre 2025 est la somme des entiers de 1 à 9 élevée au carré. Plus étonnant, 2025 est également la somme des cubes des chiffres de 1 à 9 : La découverte de cette relation étonnante est attribuée au mathématicien grec Nicomaque de Gérase qui a vécu au premier siècle de notre ère. Deux applications (conséquences) remarquables: C'est la somme des nombres de notre table de multiplication. C'est la quantité de rectangles dans une grille 9×9. SUITE 2025 >>>
Brèves associées	>>> Somme de puissances	>>> Puissances – Index
Pour en savoir plus	>>> Somme des cubes	>>> Théorème de Nicomaque de Gérase

1187. Avec ses chiffres
Nombre de Kaprekar Nombre qui est égal à la somme des deux moitiés de ses chiffres au carré. 2 025 = (20 + 25)²		Autres nombres de Kaprekar
Motifs Kaprekar avec les puissances de 45 = 20 + 25 SUITE 2025 >>>
Brèves associées	>>> Nombres de Kaprekar et leur magie		>>> Types de nombres – Index
Pour en savoir plus	>>> Nombre de Kaprekar		>>> Nombres narcissiques

1188. Partitions particulières
2 025 = 1 + 3 + 5 + … + 89		Somme des nombres impairs successifs.
Conséquence de cette partition en nombres impairs: la quantité de triangles équilatéraux élémentaires contenus dans un triangle équilatéral de côté 45 est 2025. La quantité de triangles, pointe en haut et pointe en bas, sur une ligne est égale au nombre impair suivant la quantité de la ligne du dessus. Il y en a successivement: 1, 3, 5, 7 … Or, la somme des nombres impairs est un carré.
2 025 = T44 + T45 Cas général		Somme de deux nombres triangulaires consécutifs. Identité comportant trois nombres consécutifs. Un nombre triangulaire est de la forme: Tn = ½ n (n + 1) Les premiers: 1, 3, 6, 10, 15, 21, 28 … SUITE 2025 >>>
Brèves associées	>>> Partitions – Les compter		>>> Partitions – Index
Pour en savoir plus	>>> Partitions en nombres impairs		>>> Nombres triangulaires

1189. Diviseurs
Les 15 diviseurs de 2025 {1, 3, 5, 9, 15, 25, 27, 45, 75, 81, 135, 225, 405, 675, 2025} En rouge les diviseurs unitaires. Tous les autres sont divisibles par l’un de ceux-là. SUITE 2025 >>>		Les diviseurs d'un nombre sont tous les nombres qui peuvent diviser le nombre. Ils vont par deux: Exemples: 3 x 675 ou 5 x 405. Ce sont les paires symétriques dans la liste croissante des diviseurs. Un truc simple pour savoir combien de diviseurs 2025 = 3^4 × 5^2 => (4 + 1)(2 + 1) = 15 Produit des exposants augmenté de 1.
Brèves associées	>>> Diviseurs d'un nombre		>>> Fonctions arithmétiques – Index
Pour en savoir plus	>>> Diviseurs		>>> Facteurs et diviseurs – Index

1190. Propriété des carrés
2025 = 45² = 44 × 46 + 1 Exemples 9 = 3² = 2 × 4 + 1 16 = 4² = 3 × 5 + 1 25 = 5² = 4 × 6 + 1 Pratique pour calculer un carré 7² = 6 × 8 + 1 = 49		Le carré de n est égal au produit des deux nombres entourant n plus 1: n² = (n – 1) (n + 1) + 1 En effet: (n – 1) (n + 1) = n² + n – n – 1 = n² – 1 Donc la valeur de n² est: n² = (n – 1) (n + 1) + 1 SUITE 2025 >>>
Brèves associées	>>> Carré = Somme de cubes		>>> Puissances – Index
Pour en savoir plus	>>> Propriété des carrés		>>> Carré – Index

1191. Carrés voisins
Une coïncidence comme celle que traquent les collectionneurs de nombres 2025 = 45² 4 2025 = 205² Avec deux chiffres en plus 63 2025 = 795² 91 2025 = 955² SUITE 2025 >>>		Le nombre 2025 est un carré. En le précédant d'un chiffre, il reste carré. Autres exemples avec un chiffre en plus 1225 = 35² & 8 1225 = 285² 2025 = 45² & 4 2025 = 205² 2500 = 50² & 2 2500 = 150² & 6 2500 = 250² 3025 = 55² & 9 3025 = 305² 4225 = 65² & 3 4225 = 185² 5625 = 75² & 1 5625 = 125² & 7 5625 = 275² 7225 = 85² & 2 7225 = 165²
Brèves associées	>>> Carré = Somme de cubes		>>> Puissances – Index
Pour en savoir plus	>>> Propriété des carrés		>>> Carré – Index

1192. Carré de la Bête
2 025² = 41 00625 41 + 625 = 666		Devient nombre de la bête en sommant des groupements de nombres de son carré. Nombre supposé porter malheur. C'est la racine du mal. Nombre évoqué dans l'Apocalypse de saint Jean.
Brèves associées	>>> Carré = Somme de cubes		>>> Puissances – Index
Pour en savoir plus	>>> Nombre de la Bête		>>> Ésotérisme – Index

1193. Jeu pannumérique
2 025 = 9 × 8 + 76 + 5^4 × 3 + 2 × 1 = 72 + 76 + 625 × 3 + 2 SUITE 2025 >>>		Atteindre le nombre avec des opérations arithmétiques utilisant les neuf chiffres dans l’ordre. Solution par Inder J. Taneja
Brèves associées	>>> Nombres de Harshad		>>> Types de nombres – Index
Pour en savoir plus	>>> Nombres pannumériques		>>> Motifs avec chiffres – Index

1194. Combinaisons
SUITE 2025 >>>		Carré d’un nombre du triangle de Pascal placé en ligne 10 colonne 2. C'est la quantité de combinaisons de 2 objets parmi 10. Je choisis un objet et l'un des 9 autres (9 cas); Je choisis le suivant et l'un des 8 autres (8 cas); Je choisis le troisième et l'un des 7 autres (7 cas); Etc. Bilan: 9 + 8 + 7 + 6 + 5 + 4 + 2 + 1 = 45 cas Et 45² = 2025
Brèves associées	>>> Permutations figurées		>>> Dénombrement – Index
Pour en savoir plus	>>> Combinaisons		>>> Dénombrement – Index

1195. Nombres à forte unité
2025	Il y a 2025 nombres dont l'unité est strictement plus grande que tous les autres chiffres pour les nombres de 1 à 9999. Liste: 1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 13, 14, 15, 16, 17, 18, 19, 23, 24, 25, 26, 27, 28, 29, 34, 35, 36, 37, 38, 39, 45, 46, 47, 48, 49, 56, 57, 58, 59, 67, 68, 69, 78, 79, 89, 102 … 8659, 8669, 8679, 8689, 8709, 8719, 8729, 8739, 8749, 8759, 8769, 8779, 8789, 8809, 8819, 8829, 8839, 8849, 8859, 8869, 8879, 8889. Ils sont seulement 255 avec des chiffres tous plus grands les uns que les autres. Liste: 1, 2 … 89, 123, 124, 125, 126, 127, 128, 129, 134 …2689, 2789, 3456, 3457, 3458, 3459, 3467, 3468, 3469, 3478, 3479, 3489, 3567, 3568, 3569, 3578, 3579, 3589, 3678, 3679, 3689, 3789, 4567, 4568, 4569, 4578, 4579, 4589, 4678, 4679, 4689, 4789, 5678, 5679, 5689, 5789, 6789. SUITE 2025 >>> Voir Nombre 285
Brèves associées		>>> Nombres à chiffres concaténés	>>> Types de nombres – Index
Pour en savoir plus		>>> Nombres ondulants	>>> Nombres à motifs – Index

1196. Carrés dans le cercle
2025	La quantité maximale de carrés unités alignés inclus dans un cercle de rayon 26 est 2025. À titre d'exemple, l'illustration montre le cas simple de 21 carrés unités contenus dans un cercle de rayon égal à 3 unités. Résoudre le cas général pour un rayon R donné est connu comme le problème de Gauss. SUITE 2025 >>>
Brèves associées		>>> Carrés et deux cercles	>>> Géométrie – Index
Pour en savoir plus		>>> Carrés dans le cercle	>>> Défis géométriques – Index

1197. Avec les chiffres de 2025
Avec chiffres de 2 025		Avec les chiffres de 2025 et en utilisant les opérations arithmétiques, composer des opérations dont les résultats sont les nombres successifs. Le tableau donne des exemples pour les nombres de 0 à 16. SUITE 2025 >>>
Brèves associées	>>> 200 avec neuf chiffres		>>> Jeux – Index
Pour en savoir plus	>>> Avec les chiffres de 2025		>>> Cent en chiffres

1198. Carré avec repunit en plus
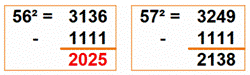
2 025 + 1111 = 3136 = 56² SUITE 2025 >>>		Curiosité avec 2025 Devient carré en lui ajoutant un repunit (nombre ne comportant que des "1"). Les nombres ayant cette propriété se calculent facilement comme le montre les deux exemples indiqués.
Brèves associées	>>> Carrés et retourné		>>> Motifs – Index
Pour en savoir plus	>>> Repunit		>>> Formes et motifs – Index

1199. Bases de numération
Le nombre 2025 est compté en base 10 car: 2 × 10^3 + 0 × 10^2 + 2 × 10^1 + 5 × 10^0 = 202510 On dit qu'il écrit en décimal ou en base 10 On peut choisir toute autre base, comme la base 8: 3 × 8^3 + 7 × 8^2 + 5 × 8^1 + 1 × 8^0 = 37518 2025 pour toutes les bases jusqu'à 30					Avec certaines bases, les nombres se répètent: 27 × 74 + 27 = 2025.. Autres ci-dessous
2, [1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1] 3, [2, 2, 1, 0, 0, 0, 0] 4, [1, 3, 3, 2, 2, 1] 5, [3, 1, 1, 0, 0] 6, [1, 3, 2, 1, 3] 7, [5, 6, 2, 2] 8, [3, 7, 5, 1] 9, [2, 7, 0, 0] 10, [2, 0, 2, 5] 11, [1, 5, 8, 1]		12, [1, 2, 0, 9] 13, [11, 12, 10] 14, [10, 4, 9] 15, [9, 0, 0] 16, [7, 14, 9] 17, [7, 0, 2] 18, [6, 4, 9] 19, [5, 11, 11] 20, [5, 1, 5] 21, [4, 12, 9]	22, [4, 4, 1] 23, [3, 19, 1] 24, [3, 12, 9] 25, [3, 6, 0] 26, [2, 25, 23] 27, [2, 21, 0] 28, [2, 16, 9] 29, [2, 11, 24] 30, [2, 7, 15] 60, [33, 45]		74, [27, 27] 80, [25, 25] 134, [15, 15] 224, [9, 9] 404, [5, 5] 674, [3, 3] 2024, [1, 1]
2025 et nombre d'or en tant que base Comme tous les nombres, le nombre 2025 peut s'exprimer en base Phi (nombre d'or). SUITE 2025 >>>
Brèves associées	>>> Base 12 – Douzaine et grosse			>>> Numération – Index
Pour en savoir plus	>>> Bases de numération			>>> Formes et motifs – Index

Suite sur le nombre 2025 en DicoNombre 2025

Retour	Brèves de maths – Page 59
Suite	Brèves de maths – Page 61 Défis mathématiques – Index Jeux et énigmes – Index
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve60.htm