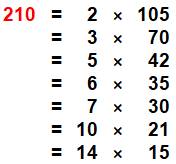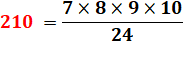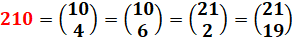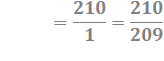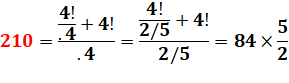Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 23/12/2023 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 50 / 100		200 à 300		300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	200	210	220	230	240	250	260	270	280	290
	210	211	212	213	214	215	216	217	218	219

Faites un double-clic pour un retour en haut de page

Deux-cent-dix

Two hundred ten

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1101 0010
Bases	31024 18111 BC18 AA20 7729
Romain	CCX

Suite en propriétés arithmétiques

Propriété remarquable

Abondant

Abondant (hautement -)

Binaire équilibré (autant de "0" que de "1")

Biscornu

Composé

Congruent

Curzon

Dihédral

Harshad

Idonéal

Intouchable

Jonction

Multi-pronique

Pair

Pratique

Primorielle

Pronique

Semi-parfait

Simple

Totient (faiblement)

Zumkeller

Géométrique

Pascal

Pentagonal (12^e)

Pentatope

Triangle (20^e)

Chiffres et numération

210 = 2^1 x 3^1 x 5^1 x 7^1	Le plus petit entier avec quatre facteurs distincts. Produit des quatre plus petits premiers. Plus petit nombre avec la signature [1, 1, 1, 1]. Nombre 4-simple de premier rang.
21010 212103 31024	Chiffres qui se suivent en base k. Tous une seule fois en base 4 (pannumérique).
210	Chiffres qui se suivent; en progression arithmétique.
210 divisible par 1, 2, 3, 10	Divisibilité avec ses chiffres ou leur somme.
210 + 12 = 222	Devient repdigit en lui ajoutant son retourné.

Addition et soustraction

210 = 27 + 28 + … + 33 = (34 + 35 + 36) x 2	Somme de consécutifs, égale à un multiple de la somme des trois suivants. Une des sept sommes de nombres consécutifs >>>
210 = 103 + 107 = 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41	Somme de premiers successifs.
210 = T20 = 1/2 (20 x 21) = 1 + 2 + 3 + ... + 19 + 20 = 5 x 6 x 7	Triangulaire & Pentagonal. Le plus petit nombre à la fois triangulaire et pentagonal (à part 1); le suivant est 40 755. L'un des six nombres triangulaires, produit de trois nombres consécutifs. Voir Brève 660

210 est un nombre triangulaire de 20 rangées

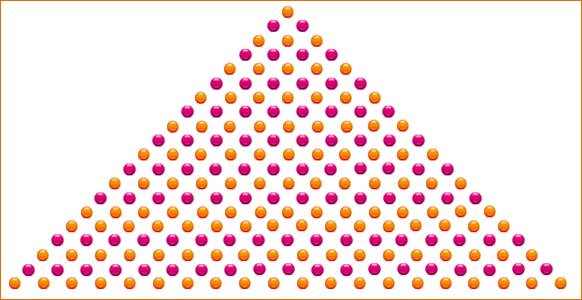
210 = 20 + 19 + 18 + … + 2 + 1

210 = T20 = T4 + T5 +…+ T10	Triangulaire, somme de nombres triangulaires.
210 = 1.2.3 + 2.3.4 + 3.4.5 + 4.5.6	Somme de produits de nombres consécutifs.
X = 1,009 … 10^92 X + k. 210 Avec k = 0, 1, 2, ... , 9	Nombres en progression arithmétique qui sont tous premiers. Voir ce Nombre

Multiplication et division

210 = 2 x 3 x 5 x 7 = 14 x 15 = 5 x 6 x 7	Plus petit nombre à quatre facteurs distincts. 30 pour deux; 2310 pour quatre. Nombre pronique et multi-pronique. Primorielle 7. Produit des 4 premiers nombres premiers. Nombre factorielle tronquée deux fois Divisible par 6 comme tout produit de trois nombres consécutifs. Biscornu Deux fois produit de nombres consécutifs. Liste: 120, 210, 720, 5040, 175560, 17297280, 19958400, 259459200, … OEIS A064224
	Sept produits à deux facteurs.
	Le produit de quatre nombres consécutifs est divisible par 24. Tous ces nombres figurent dans la cinquième diagonale du triangle de Pascal.
210 = 7! / 4!	Nombre triangulaire égal à une division de factorielles.
210 = 9! / 12^3	Factorielle divisée.
(210) = 48	Plus grand nombre ayant un totient de 48.
	La somme des diviseurs est un carré.

Avec les puissances

210 = 6^3 – 6^1 = 15^2 – 15^1	Différence de puissances d'un même nombre.
210 = 4² + 5² + 13² = 5² + 8² + 11² = 1² + 2² + 3² + 14² = 2^3 + 2^3 + 2^3 + 3^3 + 3^3	Somme de puissances.

Jeux et Combinatoire

	Ici, quatre fois nombre du triangle de Pascal. Combinaisons de 10 objets pris 4 par 4 ou 6 par 6 ou de 21 objets pris 2 par 2 ou 19 par 19. Présent plus de quatre fois dans le triangle de Pascal, en comptant les cas triviaux.
		Jeu du quatre 4. Avec la notation .4 qui vaut 0,4 = 2/5 et % qui vaut 1/100. Solution avec trois fois 4.
17 25 28 20 21 29 12 35 37 17 28 39 7 65 68	210 est l'aire de cinq triangles héroniens. Plus petite aire avec 5 configurations des longueurs des côtés.

Culture

Multimédia	210 x 297: taille en mm x mm de la page A4, format standard des feuilles de papier. On prononce: 21 - 29 - 7	>>>
Jeux	210 : surface couverte par les pièces du jeu d'hexomino.	>>>

Nombres biscornus

210 = 2 x 3 x 5 x 7 : nombres premiers vus à travers la littérature:

J'aime 210 parce qu'il est fait avec 4 nombres biscornus différents (...). Les nombres biscornus, ce sont les nombres qu'on ne peut pas couper. Comme 5 et 7. Et des grands comme 821 et 823. Ou 1721 et 1723. Dans les grands, y en a des tas qui sont deux par deux comme ça.

Le problème Turing - Harry Harrison et Marvin Minsky - Laffont

Les nombres biscornus sont, pour l'auteur, les nombres premiers

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 0, 1, 0, 0, 1, 0] 3, [2, 1, 2, 1, 0] 4, [3, 1, 0, 2] 5, [1, 3, 2, 0] 6, [5, 5, 0] 7, [4, 2, 0] 8, [3, 2, 2] 9, [2, 5, 3] 10, [2, 1, 0] 11, [1, 8, 1]	12, [1, 5, 6] 13, [1, 3, 2] 14, [1, 1, 0] 15, [14, 0] 16, [13, 2] 17, [12, 6] 18, [11, 12] 19, [11, 1] 20, [10, 10] 21, [10, 0]	22, [9, 12] 23, [9, 3] 24, [8, 18] 25, [8, 10] 26, [8, 2] 27, [7, 21] 28, [7, 14] 29, [7, 7] 30, [7, 0] 60, [3, 30]	20, [10, 10] 29, [7, 7] 34, [6, 6] 41, [5, 5] 69, [3, 3] 104, [2, 2] 209, [1, 1]

Voir Bases / Brésiliens

Retour Suite	Nombre 209 Nombre 211
Voir	Nom des nombres Nombres géométriques
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb200/Nb210.htm