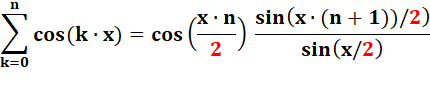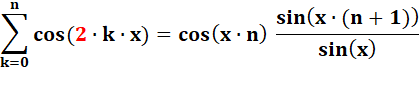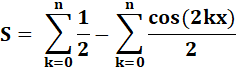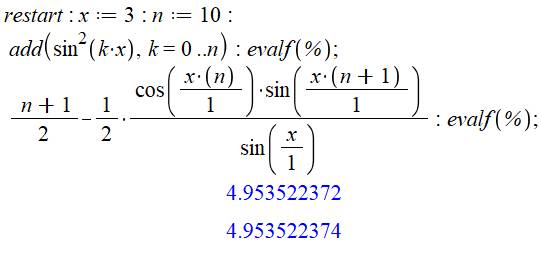Série: somme de sinus

Édition du: 13/04/2025

M'écrire

Brèves de Maths

INDEX

Sommes de nombres

Complexes

Trigonométrie

Sommation

Entiers

Puissances

Cosinus

Sinus au carré

Faites un double-clic pour un retour en haut de page

Sommation des sinus²

Comment s'y prendre pour calculer une série impliquant des sinus au carré ?
Une transformation trigonométrique, dite linéarisation, permet de passer à une forme trigonométrique sans carré; c'est une formule avec des cosinus.

Alors, cela tombe bien, nous avons développé une page qui calcule la sommation des cosinus.

Sommaire de cette page

>>> Outils – Rappels

>>> Méthode de calcul

>>> Sommation du sinus au carré

>>> Bilan

Débutants

Trigonométrie

Glossaire

Complexes

Outils – Rappels		haut
Formule du carré du sinus (linéarisation)
Somme de cosinus
Avec le facteur 2

Sans confusion possible, on omettra le point de la multiplication

Méthode de calcul		haut
Méthode du changement de monde Comment s'y prendre pour calculer une telle somme de sinus au carré ? Oui, cela n'est pas évident ! Comme on le pratique souvent en maths, la solution consiste à changer de monde (principe du levier mathématique). En l'occurrence: à passer dans le mondes des exponentielles pour y réaliser la partie calculatoire. Pour cela, on utilise les formules d'Euler. Le retour au monde trigonométrique s'effectue en inversant les formules d'Euler.	Ce qu'il faut trouver
Principe du calcul

Voir Brève 62-1230

Sommation du sinus au carré			haut
Calculer cette somme de sinus au carré.
Linéarisation.
En séparant les deux termes.
Extraction du facteur commun ½ .
Le premier terme est la somme n + 1 fois de 1 (oui: de 0 à n).
Le second terme est la somme de cosinus.
Vérification avec le logiciel Maple.

Bilan

Haut de page (ou double-clic)

Retour	Somme des cosinus Somme des entiers – Index
Suite	Nombres complexes – Index Forme matricielle Opérations
Voir	Constantes Inventaire des types de nombres Nombres – Glossaire et index Nombres réels Opérations – Index Vecteurs
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/Somsinus.htm