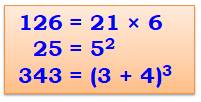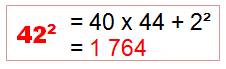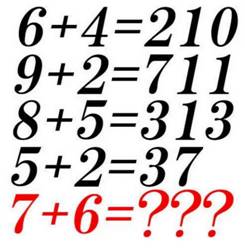NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/04/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Index général		Page 1 (1-19)		Page 2 (20-39)		Page 3 (40-59)		Page 4 (60-79)
	Page 5 (80-99)		Page 6 (100-119)		Page 7 (120-139)		Page 8 (140-159)		Page 9 (160-179)

BRÈVES de MATHS – Page 4

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

60. Nombre et ses chiffres
Nombre de Friedman On cherche des nombres qui sont égaux à une opération effectuée sur leurs chiffres. On permet les quatre opérations et toutes les autres de l'arsenal arithmétique, comme l'élévation au carré ou au cube. Chiffres dans l'ordre (exemples) 736 = 7 + 3^6 2 592 = 2^5 x 9^2		Nombre de Coster Même recherche mais en utilisant les chiffres deux fois. On n'autorise que les quatre opérations et les parenthèses. Malgré ces limitations, il est plus facile de trouver des nombres de Coster que des nombres de Friedman. Un motif répétitif (nombres terminés par 5) 25 = (2 + 2) x 5 + 5 35 = (3 + 3) x 5 + 5 Etc.
Pour en savoir plus	>>> Nombres de Friedman >>> Nombres au carré		>>> Nombres de Coster >>> Nombres au cube

61. Mesurer les triangles
Comment connaitre les longueurs dans les triangles? Pas évident! Les Anciens avaient besoin de ces données pour développer l'astronomie. Cas des longueurs des côtés Dans le triangle rectangle, le théorème de Pythagore permet le calcul du troisième côté connaissant les deux autres. Pour traiter un triangle quelconque, une hauteur le divise en deux triangles rectangles, ce qui nous ramène au cas précédent. Cas général avec longueurs et angle Toujours avec le triangle rectangle, nous connaissons la longueur d'un côté et la valeur d'un angle. Que faire pour calculer les autres grandeurs? Nous pouvons dessiner ce triangle sans difficulté et mesurer les longueurs, mais impossible de les calculer simplement. Comment s'y prendre? Utiliser des tables ou avoir recours à cette branche des mathématiques qui s'appelle la trigonométrie. En grec, trigonométrie veut dire exactement: mesure des triangles (trigonon, triangle et métron, mesure).		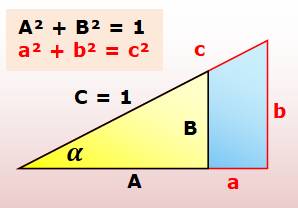Triangle de référence Le triangle (a, b, c) est plus grand que le triangle (A, B, C). Ils sont tous deux rectangles et ont le même angle alpha. L'un se déduit de l'autre par un zoom (homothétie). La trigonométrie En prenant le triangle de référence (C = 1), pour tout angle alpha, la trigonométrie donne: la valeur de A, appelée cosinus, et la valeur de B, appelée sinus. Exemple avec Alpha = 30°: A = cosinus (30°) = 0,866… B = sinus (30°) = 0,5 C = 1 (la référence) En pratique Autrefois, on trouvait ces valeurs dans les tables trigonométriques; aujourd'hui, elles sont disponibles sur les calculettes.
Pour en savoir plus	>>> Angles >>> Triangle rectangle >>> Triangle quelconque >>> Antiquité et ses savants		>>> Trigonométrie >>> Terrain de jeu de la trigo >>> Homothétie >>> Astronomie

62. Nombres 1, 3, 3, 1 – Pascal
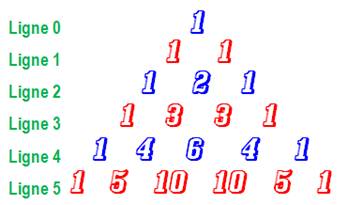
Développement des carrés Observez les coefficients d'une ligne à l'autre: chacun est la somme des deux du dessus Ex: 4 = 1 + 3 ou 6 = 3 + 3. Ces nombres sont ceux du triangle de Pascal Combinaisons Le tableau de nombres (à droite) dit "triangle de Pascal" est riche de propriétés. Notamment, il donne la quantité de choix de p objets parmi n. Ex: 3 objets parmi 5: on lit 10 possibilités en ligne 5 (numérotation à partir de 0) et en colonne 3. Remarquez que La somme des nombres sur la ligne k est égale à 2^k. En ligne 5: 1 + 5 + 10 + 10 + 5 + 1 = 32 = 2^5 Notez également cette propriété: 2^5 = 2^4 + 2^3 + 2^2 + 2^1 + 2^0 + 1 = 16 + 8 + 4 + 2 + 1 + 1		Triangle de Pascal Chaque nombre est la somme des deux du dessus. Notez la symétrie sur chaque ligne. Ce triangle était connu bien avant Pascal par les Indiens et les Chinois de l'Antiquité. Curiosité numérique avec les puissances de 11 11 = 11 11^2 = 121 11^3 = 1331 11^4 = 14641
Pour en savoir plus	>>> Triangle de Pascal >>> Développement du binôme >>> Nombre 11		>>> Triangle de Pascal et fractales >>> Combinaisons >>> Pascal (1632-1662)

63. Théorème de Fermat-Wiles: a^3 + b^3 = c^3 n'existe pas
Triplets en puissance Il existe une infinité de triplets de Pythagore impliquant le carré des nombres: 3² + 4² = 5² Par contre, aucun triplet avec le cube ou toute autre puissance supérieure. On lit: quelles que soient les valeurs de a, b, c et n supérieur à 2, il n'existe pas de nombre à la puissance n qui soit somme de deux nombres à la puissance n. Curiosités numériques		Histoire En 1637, Pierre de Fermat dit qu'il en a la preuve sans avoir la place de la noter. Ce qui est peu probable. Depuis, il existe des démonstrations pour de nombreuses valeurs particulières de la puissance n. Mais, nombreux sont ceux qui se sont attaqués à la démonstration générale, en vain. Wiles a réussi (1993), mais avec un arsenal d'outils mathématiques parmi les plus avancés d'aujourd'hui. Sa démonstration fait des incursions dans diverses rubriques très pointues des mathématiques modernes.
Brèves associées	>>> Triplets de Pythagore		>>> Prix Wolfskehl
Pour en savoir plus	>>> Théorème de Fermat-Wiles >>> Fermat (1607?-1665)		>>> Cubes = somme de cubes >>> Pépites numériques

64. Calcul mental du carré – Astuces
Premier truc simple Remplacer le calcul du carré par le produit des deux nombres voisins. C'est l'application de cette formule: n² = (n – 1)(n + 1) + 1		7² = 6 x 8 + 1 = 48 + 1 = 49 9² = 8 x 10 + 1 = 80 + 1 = 81 11² = 10 x 12 + 1 = 120 + 1 = 121 52² = 51 x 53 + 1 = 2 703 + 1 = 2 704
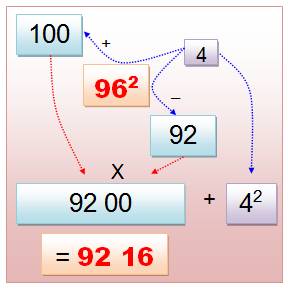
Astuce suivante – Exemple 96² = 100 x 92 + 4² = 9216 Procédé ajouter 4 pour arriver à 100 et les retrancher (92); faire le produit des deux (9200) et ajouter le carré de l'écart (4² = 16). Propriété (a + d)(a – d) + d² = a² Autre exemple:
Pour en savoir plus	>>> Carré >>> Calcul mental du carré >>> Produit de nombres consécutifs		>>> Calcul mental >>> Calcul de la racine carrée

65. Aristote (384-322 av. J-C.)
Buste d'Aristote Platon lève le doigt (ciel / idées) Aristote montre le monde réel Détail du tableau de Raphaël (1510)		Philosophe grec, Aristote laissa une œuvre considérable sur la philosophie, la logique, la politique, l'histoire naturelle et la physique. Son système montre toute la nature comme un immense effort de la matière pour s'élever jusqu'à la pensée et à l'intelligence. Élève de Platon, il nie l'existence de l'infini accessible mais accepte l'infini potentiel. II est le fondateur de la logique formelle qui a eu une grande influence sur la formation de la pensée en Europe occidentale et sur la philosophie chrétienne. Précepteur d'Alexandre le Grand. Une de ses paroles: "l'ignorant affirme, le savant doute, le sage réfléchit". Lycée et péripatéticiens En 335 av. J.-C., Aristote fonde son école rivale de l’Académie. Elle est proche du gymnase dédié à Apollon Lycien (de la province de Lycie au sud-ouest de la Turquie). Il lui donne le nom de lycée: le lycée d'Athènes. Les occupants du lycée (maîtres et disciples) avaient pour habitude de réfléchir en marchant autour du péristyle du bâtiment. On les nommait les péripatéticiens.
Brèves liées	>>> Les grands savants de l'Antiquité – B17
Pour en savoir plus	>>> Aristote >>> Citations, pensées et humour		>>> Infini >>> Logique formelle

66. Les trois filles
Énigme Je pose la devinette suivante à mon voisin: J'ai trois filles dont : Le produit de l'âge est 36, et La somme de leur âge est le numéro de votre maison. Quel est l'âge de chacune? Mon voisin réfléchit et me pose une question: Est-ce que l'aînée est blonde ? Je réponds: Oui, en effet, elle est blonde ! Alors, mon voisin me donne l'âge de chacune de mes filles.		Solution Cherchons toutes les possibilités de décomposition de 36 en 3 facteurs, et calculons la somme, en même temps: Si mon voisin me pose une question supplémentaire, c'est qu'il y a doute. Or le doute n'existe que pour la somme 13 qui est en double. La question posée est astucieuse car, en répondant: l'aînée est blonde, on signifie qu'elle est unique. Or, seul le produit 9 x 2 x 2 donne une seule fille la plus âgée. Réponse: mes filles ont 9, 2 et 2 ans.
Pour en savoir plus	>>> Les trois filles >>> Énigmes sur les familles		>>> Énigmes classiques >>> Jeux et énigmes

67. Nombres 4 – QUATRE
Écriture Manuscrite / Imprimerie / Afficheur / Arabe Propriétés Nombre pair, même doublement car son quotient par 2 est encore divisible par 2. Plus petit nombre composé. Carré de 2 , car 2 x 2 = 2² = 4 Motif exceptionnel: 2 + 2 = 2 x 2 = 4 Son carré est la différence des carrés de ses voisins: 4² = 5² – 3² Jeu des quatre 4 Imaginez une opération qui associe quatre 4 pour faire 1, 2, 3, … Ex: 4 = (4 – 4 ) x 4 + 4 5 = (4 x 4 + 4 ) / 4 100 = 4 x 4! + 4 + 4 = 4 x 24 + 2 + 2		Opération romaine (humour) Géométrie Une figure à quatre côtés est un quadrilatère dont le plus connu est le carré. Une propriété remarquable: pour n'importe quel quadrilatère, les segments qui joignent les milieux des côtés forment un parallélogramme. Topologie Le problème du coloriage d'une carte géographique avec quatre couleurs seulement à été résolu par ordinateur en 1976.
Brèves associées	>>> Nombre 3		>>> Nombre 5
Pour en savoir plus	>>> Nombre 4 – Culture >>> Nombre 4 – Maths >>> Nombre 4 – Quantité		>>> Quadrilatère >>> Carré >>> Problème des quatre couleurs >>> Jeu des quatre 4

68. Unités des puissances
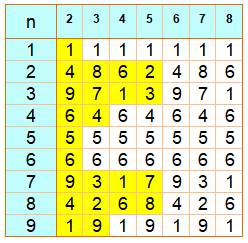
Motifs des unités des puissances Nous avons qu'un nombre terminé par 5 se terminera toujours par 5 lorsqu'il est élevé à une puissance 5^2 = 25; 15^3 = 3 375; 25^4 = 390 625 Tableau Ce tableau montre l'unité des puissances de 2 à 8 pour tous les nombres se terminant par l'unité de 1 à 9. En jaune, les seules possibilités pour chacun des chiffres. Ensuite ces chiffres se répètent. Le tableau se prolonge à droite sans fin pour toutes les puissances. La longueur de la séquence est appelée la période. Longueur de la période (Lp) Lp = 1 pour les chiffres 0, 1, 5 et 6; Lp = 2 pour les chiffres 4 et 9; et Lp = 4 pour les chiffres 2, 3, 7 et 8.			Unité des puissances 2 à 8 des nombres 1 à 9 Exemples: l'unité de 13^5 = 3 l'unité de 53^6 = 9 l'unité de 123456^789 = 6 Remarquez qu'un nombre élevé à une puissance conserve sa parité.
Exemples Unité de 19^9		19 se termine par 9 => unité = {1, 9} 9 est impair => unité = 9 En effet: 19^9 = 322 687 697 779
Unité de 123^456		123 se termine par 3 => unité = {9, 7,1, 3} 456 mod 4 = 0 => unité = 1 En effet: 123^456 = 992…561 = 9,9 10^952
On retrouve bien ces unités pour les puissances de 2 avec la période: 2, 4, 8, 6		2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 …
Pour en savoir plus	>>> Unités des puissances >>> Unités des nombres			>>> Puissances des nombres >>> Puissance de 2

69. Tables de multiplication – de 1 à 5
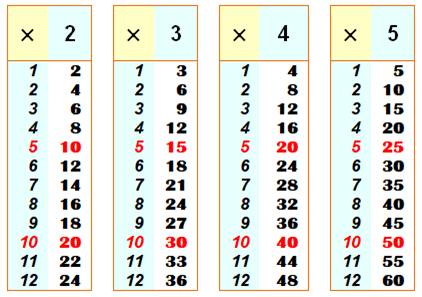
Encore utile? Connaitre les tables de multiplication reste indispensable même à l'heure des calculettes: aussi bien dans la vie de tous les jours que durant la scolarité ou la vie professionnelle. Ne serait-ce que pour estimer ou vérifier un ordre de grandeur. Table de 1, 2 et 4 La table du 1 n'est mentionnée que pour être complet. Elle est triviale (synonyme de banale en maths). 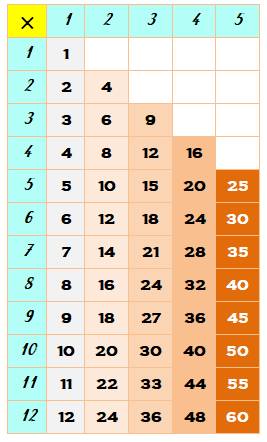La table du 2 est simple: il suffit de doubler les nombres en additionnant le nombre à lui-même: 2 x 12 = 12 + 12 = 24 Pour le 4, il faut doubler une nouvelle fois: 4 x 12 = 24 + 24 = 48 Table du 3 On double comme pour la table du 2 et on ajoute le nombre: 3 x 12 = 24 + 12 = 36 Table du 5 Après avoir ajouté un zéro, on divise par 2: 5 x 12 = 120 / 2 = 60 Lecture de la table La table du 5, par exemple, se lit en horizontal: 5, 10, 15, 20, 25; puis en vertical: 30, 35, 40, 45, 50, 55, 60. Carrés Il est utile de connaitre les carrés des nombres: 2x2 = 2² = 4; 3x3 = 3² = 9; 4x4 = 4² = 16 et 5x5 = 5² = 25. Case blanches Elles correspondent à des valeurs connues ailleurs, comme: 3 x 4 = 4 x 3 = 12.				Table de multiplication de 1 à 5 Pourquoi 12? Dans beaucoup de pays, on n'hésite pas à prolonger la table jusqu'à 12, car 11 est facile et 12 fut important dans les pays anglo-saxons et leurs unités de mesure en 12.
Tables conventionnelles Cette manière habituelle de présenter les tables permet de les réciter de façon scolaire. Écrire le tableau présenté ci-dessus est un moyen d'apprivoiser tous ce nombres; de les rendre familiers. Le but final n'est-il pas de pouvoir donner le résultat de la multiplication pour des nombres pris au hasard ?
Brèves associées	>>> Multiplication
Pour en savoir plus	>>> Table de multiplication >>> Multiplication		>>> Carrés >>> Calculette >>> Compter en 12

70. Opérations mystérieuses
Énigme Si vous pouvez résoudre ce problème de maths en une minute, votre QI est supérieur à 150 selon un utilisateur japonais de Twitter. En fait, un élève de maternelle est capable de trouver Solution Le premier chiffre du résultat est la différence des deux chiffres de l'opération: 6 – 4 = 2. Les autres à droite sont simplement la somme: 6 + 4 = 10. Ainsi, la réponse est: 7 + 6 = 113. Notez l'usage abusif du signe égal !		Vu sur le Net en septembre 2017
Brèves associées	>>> Les trois filles
Pour en savoir plus	>>> problèmes 2017 qui affolent le Net >>> Quotient intellectuel (QI)		>>> Énigmes classiques >>> Jeux et énigmes

71. Les 23 problèmes de Hilbert
David Hilbert (1862-1943) – Allemand Un des plus grands mathématiciens du XX^e siècle. En 1895, il arrive à l'université de Göttingen qu'il ne quittera pas. En 1900, au Second Congrès International des Mathématiciens réunis à Paris, il propose 23 problèmes non résolus à la communauté des mathématiciens. Citation L'art des mathématiques consiste à trouver le cas particulier qui contient tous les germes de la généralité – David Hilbert		En 2017, il y a : 11 problèmes résolus; 5 problèmes non résolus; 7 problèmes partiellement résolus ou indécidables ou de formulation pas assez précise. Type de problèmes Hypothèse du continu; Consistance de l'arithmétique; Découpe des polyèdres; Axiomatisation de la phyique; Conjecture de Riemann sur les nombres premiers; Algorithme de résolution des équations diophantiennes; Etc.
Pour en savoir plus	>>> Les 23 problèmes de Hilbert >>> Contemporains de Hilbert >>> Citations sur les mathématiques		>>> Hilbert – Biographie >>> Hypothèse du continu >>> Histoire – Index

72. Rien – Humour
	Parler pour ne rien dire – Sketch de Raymond Devos (1922-2006) – Transcription à partir d'un enregistrement.
Pour en savoir plus	>>> Humour – Index >>> Expression avec zéro, rien, nul …	>>> Rien / Vide

73. L'énigme des 30 euros
Historique Il s'agit d'un problème très ancien qui déroutait nos anciens lors de leurs soirées divertissantes. Problème Trois amis paient leur consommation 10 euros chacun. S'agissant de jeunes, le patron leur fait une ristourne de 5 euros. C'est la serveuse qui en est chargée. Fort embarrassée pour faire la division, elle rend 1 euro à chacun et garde le reste. Jusque là rien de spécial. Sauf que la serveuse calcule: chaque personne à payé 10 – 1 = 9 euros. Si j'ajoute les 2 euros que j'ai gardés, ça fait un total de 29 euros. Elle se demande encore où est passé le dernier euro pour faire 30. Évidemment, elle n'en parle pas au patron.		L'énigme! Cette petite histoire est bien plaisante, mais sauriez-vous aider la serveuse à résoudre cette énigme qui la ronge. Où est passé cet euro manquant?
		Solution L'embrouille vient d'un mauvais calcul, mélangeant l'argent reçu et l'argent donné. 27 + 2 à comparer à 30, c'est faux; 27 – 2 à comparer à 25 c'est juste, c'est ce que touche le patron (30 euros moins la ristourne de 5 euros). Les 27 euros déboursés par les trois amis servent à payer les consommations (25 euros) et ce que la serveuse à conservé (2 euros).
Pour en savoir plus	>>> Énigme des 30 euros		>>> Énigmes – Index

74. Addition de nombres entiers
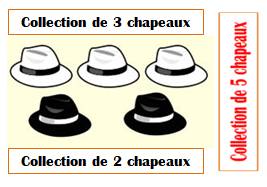
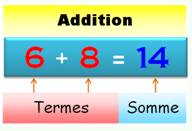
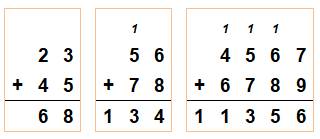
Principe L'addition consiste à rapprocher des collections d'objets et à compter les objets de la nouvelle collection. On note: 3 + 2 = 5 Addition Additions amusantes 888 + 88 8 + 8 + 8 = 1000 (avec huit 8). 1 + 2 + 3 – 4 + 5 + 6 + 78 + 9 = 100 (avec tous les chiffres et … une soustraction)		Addition posée On ajoute les chiffres colonne après colonne en commençant par la droite. Si la valeur comporte une dizaine, celle-ci est notée en haut de la colonne suivante (la retenue). Addition en ligne 23 + 45 + 56 + 19 = 143 19 + 56 + 45 + 23 = 143 La somme ne change pas si on change l'ordre des opérations (commutativité). Additions et parenthèses (23 + 45) + (56 + 19) = 143 Les parenthèses sont inutiles Somme des nombres de 1 à n 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 Utilisation de la commutativité et des parenthèses: (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 10 + 5 = 55
Brèves associés	>>> Somme des nombres de 1 à n
Pour en savoir plus	>>> Addition >>> Opérations – Index		>>> Faire 1000 avec huit 8 >>> Faire 100 avec tous les chiffres

75. Rosace – Hexagone
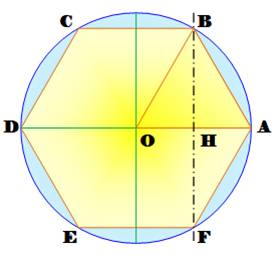
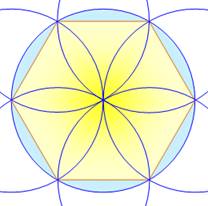
Hexagone inscrit dans un cercle L'hexagone est découpé par six triangles tels que OAB. Or, deux de ses côtés sont des rayons du cercle; ils ont la même mesure; le triangle est isocèle. Un angle au sommet comme AOB se retrouve six fois pour 360°; chacun vaut 60°. Le triangle est équilatéral et: OA = OB = AB Dans un hexagone régulier, la longueur du côté est égale au rayon du cercle circonscrit.		Construction de la rosace et de l'hexagone régulier (selon la propriété énoncée à gauche) Un cercle de centre O et un point quelconque A. Gardez la même ouverture du compas et tracez le cercle de centre A. Il coupe le cercle d'origine en B. De ce point, recommencez l'opération. Ainsi de suite, six fois. Cosinus 60° = ½ Dans le triangle OAB, BF est une médiatrice; Avec OA = 1, OH = HA = ½ = cosinus de l'angle 60°. Bonne astuce pour dessiner un angle de 60°!
Pour en savoir plus	>>> Hexagone >>> Étoile à six branches >>> Constructions – Index		>>> Triangle équilatéral >>> Médiatrice >>> Cosinus

76. 123456789 – Divisibilité
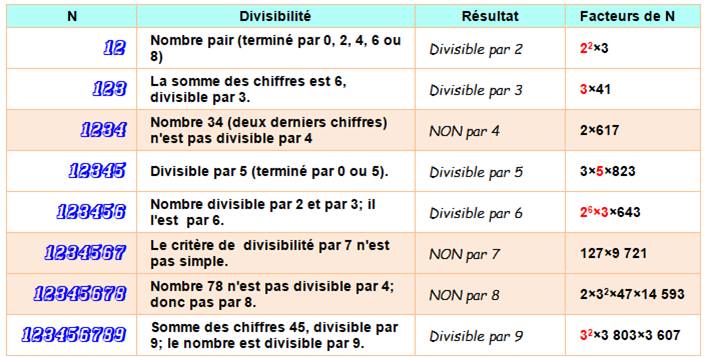
Devinette Laquelle de ces affirmations est fausse? Trouvez la réponse sans effectuer les divisions. Prolongez la recherche.		Affirmations 12 est multiple de 2. 123 est multiple de 3. 1234 est multiple de 4. 12345 est multiple de 5. 123456 est multiple de 6.
Réponse: l'affirmation 3 est fausse
Pour en savoir plus	>>> Critères de divisibilité >>> Diviseurs et facteurs		>>> Nombre 123456789

77. Triangles et polygones – n x 180°
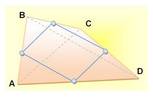
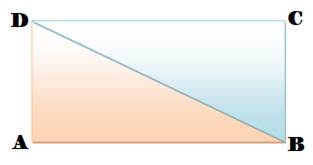
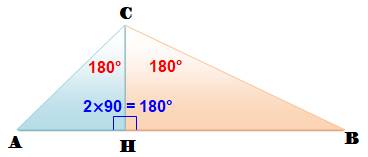
Somme des angles du rectangle Dans le rectangle ABCD, chaque angle au sommet est un angle droit (90°). La somme vaut 4 x 90 = 360°. Somme des angles dans le triangle rectangle La diagonale coupe le rectangle en deux triangles rectangles égaux. La somme des angles dans chaque triangle vaut 360 / 2 = 180°. La somme des deux angles non-droits du triangle rectangle est égale 90°.		Somme des angles dans le triangle quelconque Une hauteur du triangle le partage en deux triangles rectangles. La somme des angles vaut 2 x180°. Parmi les angles sont comptés les deux angles droits en H. La somme des angles du triangle ABC est égale à 360 – 180 = 180° La somme des angles d'un triangle quelconque est égale à 180°.
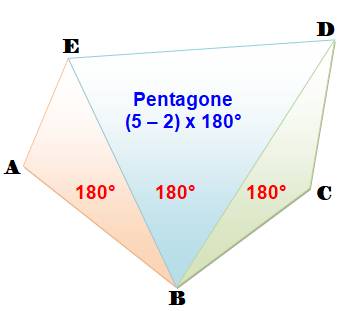
Somme des angles d'un polygone à n côtés Tout polygone convexe peut être partagé en n – 2 triangles quelconques dont la somme des angles de chacun vaut 180°. Par exemple, le pentagone avec n = 5 est partagé en trois triangles et la somme des angles vaut 3 x 180 = 540°. La somme des angles du polygone convexe quelconque à n côtés est égale à (n – 2) x 180°. Quadrilatère: 2 x 180° Pentagone: 3 x 180° Hexagone: 4 x 180°
Brèves associés	>>> Triangle rectangle
Pour en savoir plus	>>> Somme des angles du triangle >>> Somme des angles des polygones		>>> Rectangle >>> Polygone

78. L'Univers – 13,7 millards d'années
Forme L'univers est incroyablement grand. On se sait pas s'il est fini ou infini. Si sa courbure est égale à 1, il est plat et infini; si elle est légèrement supérieure, l'Univers est sphérique. Or les dernières mesures (WMAP) révèlent une courbure entre 0,9937 et 1,0178. L'espace-temps est décrit par trois dimensions spatiales et une dimension temps. Il est déformé par la présence de masses et d'énergie (relativité générale). Origine et taille Il est âgé de 13,7 milliards d'années, date à laquelle s'est produite une gigantesque explosion, le Big Bang. Notre étoile, le Soleil, n'est apparue qu'il y a 4, 5 milliards d'années. Quelques temps après l'explosion originelle, la lumière s'est rependue dans toutes les directions à mesure que l'Univers grossissait. Les télescopes spatiaux modernes (Planck) ont réussi à capter cette lumière (image) appelée fond diffus ou rayonnement fossile. Aujourd'hui, nous ne pouvons observer l'Univers que partiellement; uniquement les parties desquelles la lumière a pu nous parvenir. Soit une distance maximale de 13,7 milliards d'années de lumière. Si nous en avions les moyens, il serait possible de "voir" jusqu'à 93 milliards d'années de lumière (Univers visible, mais non-observable).		Évolution Non seulement l'Univers n'a pas fini de croître (expansion), mais il accélère! Phénomène mis en évidence en 1998. Composition 68,3% d'énergie noire dont on ne sait pas grand-chose. 26,8% de matière noire due à des particules exotiques? Si oui, elles sont encore inconnues. 4,9% de matière visible ou ordinaire, seule bien connue. Celle qui compose les étoiles et les planètes. Matière visible Les étoiles, comme notre Soleil, se regroupent en galaxies (photo). Il y aurait 2 000 milliards de galaxies dans l'Univers observables (Hubble – 2016). Notre Galaxie (la Voie lactée) compte 400 milliards d'étoiles. Soit, en extrapolant: 2.10^12 x 4.10^11 = 8.10^23 étoiles (un 8 suivi de vingt-trois 0). Il y aurait plus d'étoiles dans l'Univers observable que de grains de sable sur les plages de toute la Terre.
Pour en savoir plus	>>> L'Univers >>> Big Bang >>> Galaxies >>> Relativité générale	>>> Étoiles et grains de sable >>> Masse manquante >>> Vitesse de la lumière

79. Magie: âge répété
Tour de magie (deux chiffres) Je vais répéter quatre fois ton âge. Inscris ton âge sur la calculette : 76 Multiplie par 13 837: 1 051 612 Multiplie encore par 73: 76767676 Génial, non ?		Explication : Je multiplie: 13 837 x 73 = 1 01 01 01 Je multiplie: 76 x 01 01 01 01 = 76 76 76 76 Facteurs de 1 010 101
Autre possibilité (un chiffre) Je vais répéter trois fois un nombre de 1 à 9. Inscris un chiffre sur la calculette: 4 Multiple par 37: 148 Puis par 3: 444		Explication avec les facteurs de 111 Note: Je sais tout de suite que 111 est divisible par 3, car la somme des chiffres (1 + 1 + 1 = 3) est divisible par 3.
Brèves associés	>>> Divisibilité		>>> Énigme des trois filles
Pour en savoir plus	>>> Magie – Index >>> Énigmes – Index >>> Énigmes pour Juniors (diaporama)		>>> Facteurs et diviseurs >>> Nombre 111 >>> Nombre 1 010 101

Retour	Brèves de maths – Page 3
Suite	Brèves de maths – Page 5
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve04.htm