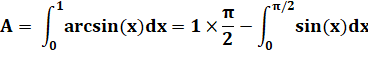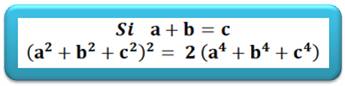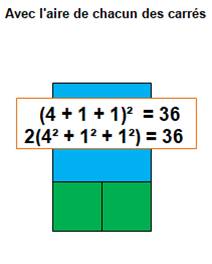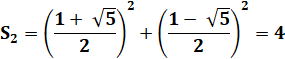Brèves de maths 40

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Page 40 (780-799)		Page 41 (800-819)		Page 42 (820-839)		Page 43 (840-859)		Page 44 (860-879)
	Page 45 (880-899)		Page 46 (900-919)		Page 47 (920-939)		Page 48 (940-959)		Page 49 (960-979)

BRÈVES de MATHS – Page 40

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

780. Aire du poisson
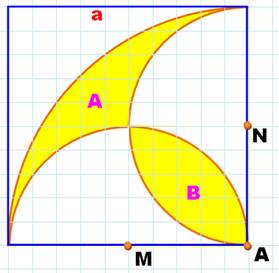
Énigme Un carré (bleu) de côté a. Un grand quart de cercle (A; R = a). Deux petits demi-cercles (M et N; R = a/2). La figure en jaune, qui ressemble à un poisson, est partagée en deux parties A et B. Comparez les aires. Solution		Alex Bellos cite cette énigme sous le nom: L'aile et la lentille
Brèves associées	>>> Aires dans le quart de cercle		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Aires des figures dans les cercles		>>> Aires – Index

781. Points dans le carré
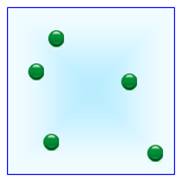
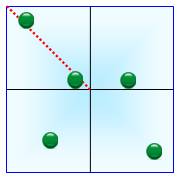
Problème Un carré de côté 1. Cinq points internes ou sur le périmètre. Montrer qu'il existe au moins une paire de points éloignés au maximum de Solution Dessiner les médianes qui partagent le carré en quatre carrés identiques. Avec quatre régions à remplir avec cinq points, selon le principe des tiroirs, il existe au moins deux points dans le même petit carré. Or, la longueur de la diagonale du petit carré est .
Brèves associées	>>> Triangles dans le triangle	>>> Brèves Dénombrement – Index
Pour en savoir plus	>>> Principes des tiroirs – Exemples	>>> Dénombrement – Index

782. Intégrale amusante avec sinus
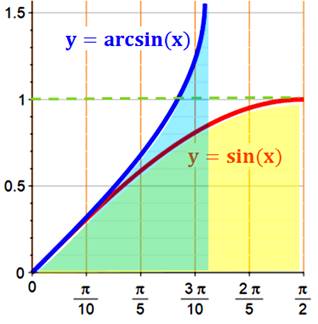
Propriétés Les graphes des fonctions y = sin(x) et y = arcsin(x) sont symétriques. Comment calculer l'aire bleue ? Aire sous les courbes Zone bleue = rectangle sous pointillés verts – zone jaune Primitive de sinus = – cosinus		Graphe Chacune des aires sous courbe (en bleu et en jaune) vaut 0,570…
Brèves associées	>>> Intégrale ln(x) et exp(x)		>>> Brèves Analyse – Index
Pour en savoir plus	>>> Calcul intégral		>>> Primitives

783. Somme symétrique des entiers
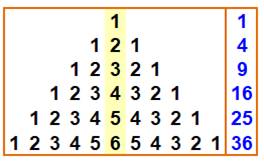
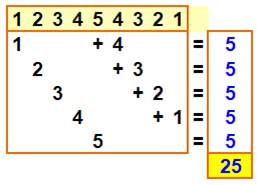
Exemples de sommes La somme symétrique des entiers centrée sur n est le carré de n.		Mécanisme de formation du carré Formule 1 + 2 +… + (n–1) + n + (n–1) +…+ 2 + 1 = n²
Brèves associées	>>> Somme des entiers		>>> Brèves Suites – Index
Pour en savoir plus	>>> Somme des entiers – Calculs		>>> Sommes des entiers – Introduction

784. 1 + 1/2 + 1/3 + … 1/n: entier ?
Problème Montrer que: n'est jamais un entier pour n un entier positif.		Solution Mettre toutes les fractions au même dénominateur. Exemple Tous les termes au numérateur sont pairs sauf le dernier. La somme est impaire. Le dénominateur est pair. L'un ne peut pas diviser l'autre. L'expression n'est jamais un nombre entier.
Brèves associées	>>> Somme des puissances de 9		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Cas de 1 + 1/2 + 1/3 + … + 1/n		>>> Types de nombres – Index

785. Horloge en 8
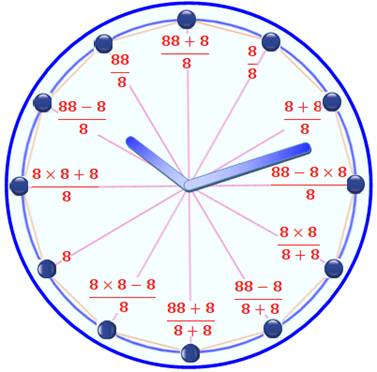
Horloges en "8" Horloges sur lesquelles on a remplacé les nombres ordinaires par des expressions mathématiques. Ici, application d'un jeu qui consiste à obtenir un nombre donné avec un minimum de "8". Comme: 1000 = 8 + 8 + 8 + 88 + 888 Simplification des calculs sur le cadran Remplacer les 8 par des 1, sauf le deuxième 8 dans une multiplication et faites le calcul simple: Comme: (88 + 8) / 8 = (11 + 1) / 1 = 12 Horloges à cadran mathématique Parfois, concours d'ingéniosité pour trouver une expression algébrique à deviner. Comme:		Les aiguilles d'une horloge en démonstration montrent souvent une heure voisine de 10h 10 qui, sans doute, rappelle le sourire.
Brèves associées	>>> Horloges mathématiques >>> Horloge romaine – Énigme		>>> Brèves Jeux – Index
Pour en savoir plus	>>> Horloges mathématiques >>> Horloge – Fonctionnement		>>> Faire 1000 avec des "8" >>> Nombre 8

786. Somme de carrés de sinus
Calcul d'une somme qui parait inatteignable. Un peu de réflexion et l'astuce paie ! On utilisera deux propriétés trigonométriques: sin²(a) + cos²(a) ) = 1 et sin(a) = cos(90° – a) Rappel: sin(45°) = cos(45°) = rac(2)/2 et son carré vaut 1/2.
Brèves associées	>>> Valeurs trigonométriques principales	>>> Brèves Trigo – Index
Pour en savoir plus	>>> Relations trigonométriques	>>> Trigo en première

787. Cercle externe au triangle
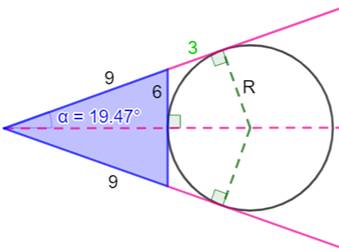
Problème Un triangle isocèle (9, 9, 6). Un cercle tangent externe à la base. Quel est son rayon ? Résolution par calculette
Résolution littérale		Ce calcul est de niveau supérieur. Il fait intervenir la notion arcsinus: la fonction réciproque du sinus qui indique la valeur de l'angle connaissant le sinus. Encore mieux, ici c'est la tangente d'un arcsinus, la tangente d'un angle (thêta) que l'on ne connait que par son sinus (x).
Brèves associées	>>> Cercles et triangles équilatéraux		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Cercles inscrits >>> Triangle isocèle		>>> Arcsin, arcos …

788. Formule du triple quad
Sorte de théorème de Pythagore appliqué à des segments et non des triangles
Application Trois carrés, dont deux qui s'appuient sur l'un des côtés du troisième. Dans cet exemple: un carré de côté 2 et aire 4, et deux carrés de côté 1 et aire 1. On compare les deux sommes des aires en notant a, b et c les longueurs des côtés: Ces deux sommes sont égales chaque fois que a + b = c		Exemples
Brèves associées	>>> Quadrature du triangle		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Formule du triple quad		>>> Théorème de Pythagore

789. Trigonométrie rationnelle
Une forme particulière de la trigonométrie, de la science des mesures notamment dans le triangle. Elle a la particularité de ne pas utiliser de nombres irrationnels: ni nombre Pi, ni racines carrées. Toutes les grandeurs sont exprimées par des fractions. Son auteur, N.J. Wildberger affirme que cette trigonométrie est plus pratique et permet de résoudre plus simplement certains problèmes de géométrie.
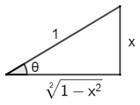
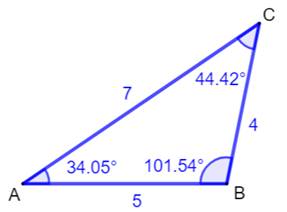
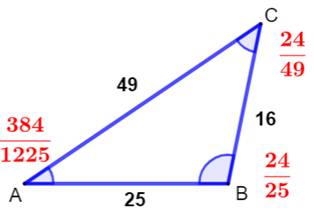
Traditionnelle Les côtés du triangle sont définis par leur longueur. Les angles par leur valeur en radians ou en degrés; généralement des nombres avec décimales, ici tronquées à deux.		Rationnelle Les côtés du triangle sont définis par le carré de leur longueur: la quadrance. Les angles par une fraction qui équivaut au carré du sinus de l'angle: l'ouverture (spread en anglais)

Brèves associées	>>> Calcul avec les cosinus		>>> Brèves Trigonométrie – Index
Pour en savoir plus	>>> Trigonométrie rationnelle >>> Trigonométrie classique		>>> Nombres irrationnels

790. Dates à chiffres distincts
On note les dates avec les huit chiffres comme le 1^er janvier 2020 en 01 01 2020. Quelles sont les dates pour lesquelles les huit chiffres sont différents ? S'il en existe beaucoup, la période autour de l'année 2000 est vide comme le montre les deux dates indiquées.		Dernière date: 25 06 1987 Prochaine date: 17 06 2345
Brèves associées	>>> Date palindrome		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Date à chiffres distincts		>>> Nombre 2013

791. Courbes d'Edwards
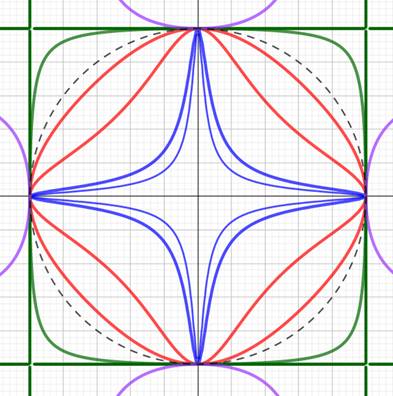
Harold Edwards a étudié ce genre de courbes en 2007. Ce sont des courbes elliptiques. Application en cryptographie par Daniel J. Bernstein et Tanja Lange. Dans ce cadre, elles seraient plus avantageuses que les courbes plus connues de Weierstrass. Équations de ces courbes Courbes bleues: k = 1000 (interne) et 300. Courbes rouges: k = 10 puis 1. Courbe noire: k = 0 (cercle) Courbe verte: k = – 0,9 puis 1 (carré) Courbe violette: k = – 2 (externe)
Brèves associées	>>> Équations et Racines – Un truc!	>>> Brèves Équations – Index
Pour en savoir plus	>>> Approche de l'elliptique >>> Courbes elliptiques d'Edwards	>>> Carré >>> Cryptographie

792. Nombre d'or, Fibonacci et Lucas
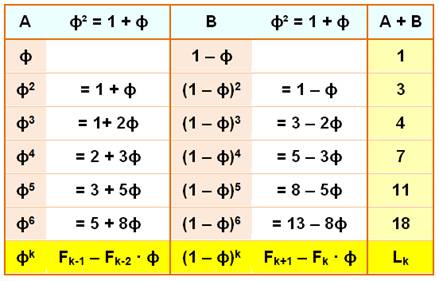
Le nombre d'or (ϕ), lorsqu'il est élevé à la puissance k, cultive une relation à la fois avec la suite de Fibonacci et celle de Lucas On a, par exemple, sur le ligne 2 du tableau: Ou, avec la valeur du nombre d'or: Ou, avec la valeur du nombre d'or: La suite de telles sommes est la suite de Lucas: 1, 3, 4, 7 …
Brèves associées	>>> Fibonacci et nombre d'or	>>> Brèves Équations – Index
Pour en savoir plus	>>> Fibonacci et Lucas	>>> Nombre d'or >>> Puissances du nombre d'or

793. Diagonale du tableau
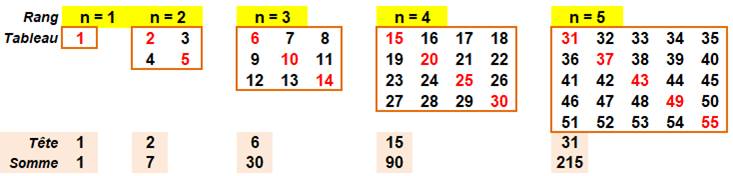
Une succession de tableaux carrés contenant les nombres successifs. Le premier nombre en tête du tableau est donné par la formule en T_n. La somme des valeurs sur la diagonale rouge est donnée par la formule en D_n. La référence en "pour en savoir plus" explique la méthode de calcul.

Brèves associées	>>> Somme des carrés	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Somme sur les diagonales	>>> Matrices

794. Cycle de Collatz généralisé
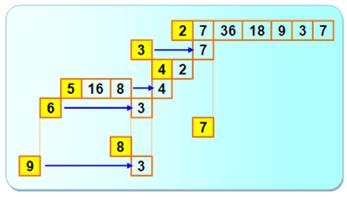
Transformation d'un nombre On connait la transformation 3x + 1 dite de Syracuse ou de Collatz. Simple mais encore pleine de mystères. Celle-ci, dite généralisée, crée une image du nombre selon qu'il composé ou premier. Voir ci-dessous. Exemples 3 est premier => 3 x 2 + 1 = 7 4 est composé => 4 / 2 = 2		Trajectoire d'un nombre Comme pour le cas classique, les images trouvées sont réinjectées dans le processus jusqu'à trouver un point d'arrêt ou un cycle qui boucle sur lui même. Exemples de trajectoire 17, 222, 111, 37, 1148, 574, 287, 41, 1518, 759, 253, 23, 438, 219, 73, 5184, 2592, 1296, 648, 324, 162, 81, 27, 9, 3, 7, 36, 18, 9 La trajectoire du nombre 17 se termine par un cycle en 9 On ne sait pas si la trajectoire du nombre 47 a une fin.
Procédé Collatz			Trajectoire des nombres de 2 à 9
Brèves associées	>>> Cycle de Collatz			>>> Brèves Itérations – Index
Pour en savoir plus	>>> Cycle de Collatz généralisé			>>> Cycle de Collatz

795. Le singe et les noix de coco
Énigme Énigme dont l'énoncé est simple mais pas facile à résoudre sans un bagage du niveau de la terminale ou supérieur. Il existe une infinité de solutions dont la plus petite est 3 121 noix de coco. Suivre le lien indiqué pour l'explication de la solution en images et en calculs.		Énoncé de l'énigme Cinq hommes et un singe font une provision de noix de coco. Durant la nuit le premier se lève et prend un cinquième des noix de coco; il en reste une qu'il donne au singe. Le deuxième se lève un peu plus tard et fait la même chose: il prend un cinquième de qui reste et en donne une au singe. Même chose jusqu'au cinquième. La troupe se lève au petit matin comme si de rien n'était; chacun se sent coupable et ne dit rien. Ils décident de faire le partage à parts égales. Chacun reçoit sa part et il ne reste pas de noix de coco. Combien de noix de coco au départ?
Brèves associées	>>> Le fortin et ses gardes		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> SOLUTION de l'énigme		>>> Bananes et chameaux

796. Division qui retourne
Division magique Imaginez un nombre qui commence par le chiffre k et qui, divisé par k, retourne le même nombre avec le chiffre k passant de tête en queue. C'est le cas du nombre 410 256. Le procédé de formation est simple (se reporter au lien ci-dessous). Il existe un nombre unique pour tout k de 2 à 9. Celui avec k = 4 est le plus court avec 6 chiffres, avec k = 6, il est le plus long avec 58 chiffres.		Tête en queue avec 4 Cas k = 8, 13 chiffres 8101265822784 / 8 = 1012658227848
Brèves associées	>>> Nombre 153 et cycle-cube		>>> Brèves Itérations – Index
Pour en savoir plus	>>> Divisions qui retournent		>>> Procédé de Kaprekar

797. Nombres en 100…1
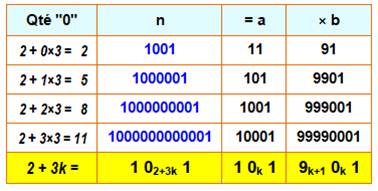
Trouver les diviseurs Un truc pour trouver les diviseurs de ces nombres en 100…1. Le nombre 1001 est divisible par 11. Le nombre 100 000 1 est divisible par 1 0 1. Le nombre 10^3(k+1) + 1 est divisible par 10^{k + 1} + 1. Si le nombre compte 2 + 3k zéros, il est divisible par un nombre avec 1 + k zéros entouré de 1. Le quotient est un nombre en 99..00..1.		Un nombre en 100..1 avec 2 + 3k zéros est de la forme 10^3(k+1)
Brèves associées	>>> Nombre 153 et cycle-cube		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Nombres en 100…1		>>> Divisibilité par 11

798. Divisibilité par 37
Procédé expliqué sur un exemple. Partager le nombre en blocs de trois chiffres. Ajouter les nombres de deux chiffres de droite. Ajouter les chiffres de gauche et multiplier par 11. Si la différence est divisible par 37, le nombre l'est aussi.		Exemple de calcul de divisibilité par 37 La différence des deux sommes est nulle, le nombre est divisible par 37: 4 567 872 = 37 x 123456
Brèves associées	>>> Divisibilité par 137		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Divisibilité par 37 – Explications		>>> Nombre 37

799. Isoler les chiffres avec tableur
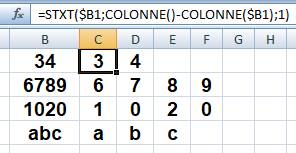
Principe L'Instruction STXT permet l'extraction d'un groupe de caractères dans une chaine ou un nombre. L'instruction COLONNE renvoie le numéro de la colonne de la cellule indiquée ou de la colonne courante (). Le numéro du chiffre à extraire progressera comme le numéro de la colonne où il sera placé. Procédé Utiliser l'instruction d'extraction STXT en précisant: la position où se trouve le nombre à éclater; adresse absolue en colonne ($) et relative en ligne. le rang du chiffre à extraire par lecture des numéros de colonne: numéro de la colonne en cours (), moins numéro de la colonne où se trouve le nombre ($B1) la quantité de chiffres à extraire (1).		La formule est valable pour toutes les lignes. Utiliser la poignée en bas à droite pour copier la formule dans la zone voulue.
Brèves associées	>>> Quantité de chiffres		>>> Brèves Méthodes – Index
Pour en savoir plus	>>> Tableur – Quelques trucs		>>> Isoler les chiffres par programme

Retour	Brèves de maths – Page 39
Suite	Brèves de maths – Page 41
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve40.htm

780. Aire du poisson

781. Points dans le carré

782. Intégrale amusante avec sinus

783. Somme symétrique des entiers

784. 1 + 1/2 + 1/3 + … 1/n: entier ?

785. Horloge en 8

786. Somme de carrés de sinus

787. Cercle externe au triangle

788. Formule du triple quad

789. Trigonométrie rationnelle

790. Dates à chiffres distincts

791. Courbes d'Edwards

792. Nombre d'or, Fibonacci et Lucas

793. Diagonale du tableau

794. Cycle de Collatz généralisé

795. Le singe et les noix de coco

796. Division qui retourne

797. Nombres en 100…1

798. Divisibilité par 37

799. Isoler les chiffres avec tableur