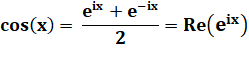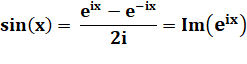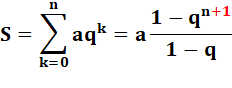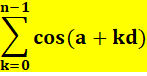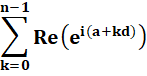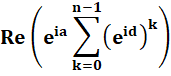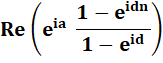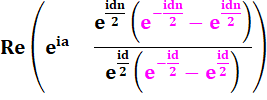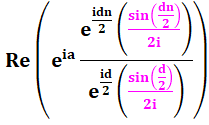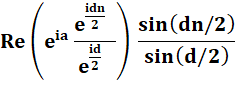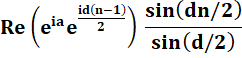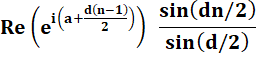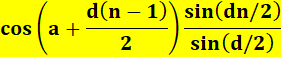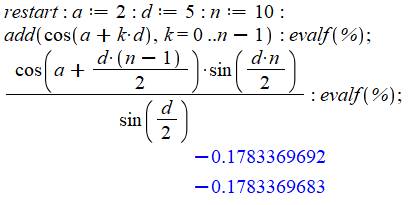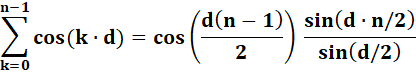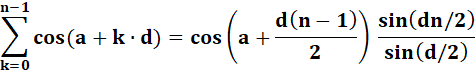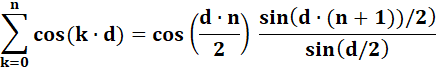Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 13/04/2025 M'écrire Brèves de Maths

INDEX Sommes de nombres Complexes Trigonométrie	Sommation
	Sommation	Entiers	Puissances
	Cosinus	Sinus au carré

Faites un double-clic pour un retour en haut de page

Sommation des cosinus Comment s'y prendre pour calculer une série impliquant des cosinus? Nous allons faire appel à Euler et à ses formules, lesquelles permettent de passer du monde de la trigonométrie à celui des exponentielles. Une fois arrivé dans le monde des exponentielles, les calculs sont plus pratiques même s'il nécessite, en l'occurrence, un peu d'imagination (d'intuition, d'astuce …). Calculs faits, on revient au monde de la trigonométrie, toujours en utilisant les formules d'Euler.
	Sommaire de cette page >>> Outils – Rappels >>> Sommation du cosinus >>> Bilan	Débutants Trigonométrie Glossaire Complexes

Outils – Rappels		haut
Formes des nombres complexes
Formule d'Euler
Expression du cosinus (Re = partie réelle)
Expression du sinus (Im = partie imaginaire)
Série géométrique de raison q et de premier élément a. Sommation de 0 à n.
Règle des exposants

Sommation du cosinus		haut
Calculer cette somme de cosinus pour k de 0 à n – 1 . L'angle (a + kd) progresse de façon arithmétique avec la raison d.
Expression exponentielle.
Extraction des parties constantes de la somme. Notez que e^ikd = (e^id)^k
La somme est une série géométrique de raison e^id . Notez que la sommation va jusqu'à n – 1 (et non n).
ASTUCE ! ou intuition … Mise en facteur avec angle moitié. Façon de faire apparaitre la forme exponentielle d'un sinus.
Remplacement pas les sinus. De sorte que la formule finale va effectivement impliquer des angles moitiés (d/2).
Simplification des fractions en sinus. Disparition de la partie imaginaire. La fraction en sinus est réelle.
Simplification des fractions en exponentielles. L'exposant en dénominateur devient négatif en le faisant passer au numérateur.
Regroupement des exponentielles. Le produit des exponentielle entraine une somme des exposants.
La partie réelle de l'exponentielle est un cosinus.
Vérification avec le logiciel Maple.

Bilan

En bilan selon la présence de la constante a.
Borne n

Haut de page (ou double-clic)

Retour	Somme des entiers – Index
Suite	Nombres complexes – Index Forme matricielle Opérations
Voir	Constantes Inventaire des types de nombres Nombres – Glossaire et index Nombres réels Opérations – Index Vecteurs
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/Somcosin.htm